Моделирование является важным инструментом в различных областях науки, индустрии и искусства. Однако создание модели - это только половина дела. Чтобы модель была полезной и имела практическое применение, необходимо определить меры и параметры, с помощью которых будут измеряться ее характеристики.
Меры моделей подразумевают численные значения, с помощью которых можно оценить различные аспекты модели. Например, меры могут быть связаны с точностью, стабильностью, надежностью или скоростью модели. Они позволяют оценить величину этих характеристик и сравнить разные модели между собой.
Кроме того, модели имеют параметры, которые представляют собой входные данные или настройки модели. Параметры определяют характеристики модели, которые могут быть изменены, чтобы получить различные результаты. Например, в модели автомобиля параметром может быть скорость или расход топлива.
Значимость мер и параметров моделей связана с несколькими факторами. Во-первых, они позволяют установить критерии и ограничения для разработки и использования модели. Без мер и параметров модель может быть бесполезной и неэффективной. Во-вторых, они позволяют сравнивать разные модели и выбирать наиболее подходящую для конкретной задачи. Наконец, меры и параметры моделей помогают в анализе и оценке результатов моделирования, а также в определении надежности и точности модели.
Роль моделей в научном исследовании
Модели имеют важное значение в научных исследованиях, поскольку они позволяют упростить и анализировать сложные явления и процессы. Модели используются во многих областях науки, включая физику, химию, биологию, экологию и другие.
Роль моделей заключается в том, чтобы представить реальные явления и процессы в упрощенной форме. Модели могут быть математическими, графическими, физическими или компьютерными. Они позволяют исследователям изучать различные аспекты явлений, изменять параметры и измерять результаты экспериментов.
Одной из главных задач моделей является предсказание поведения реальных систем и процессов. Модели могут быть использованы для прогнозирования погоды, расчета движения тела или определения вероятности наступления определенного события. Например, модели климата позволяют ученым предсказывать изменения климата в будущем и оценить возможные последствия для окружающей среды и человечества.
Модели также используются для проверки гипотез и теорий. Исследователи могут создавать модели, основанные на определенной теории, и сравнивать результаты моделирования с реальными данными. Если модель соответствует наблюдаемым данным, это может подтвердить верность теории. В противном случае, исследователи могут изменять модель или теорию, чтобы она была более точной и соответствовала наблюдениям.
Кроме того, модели могут использоваться для обучения и объяснения сложных понятий. Используя модели, преподаватели могут помочь студентам понять абстрактные концепции, визуализировать процессы и взаимодействия между различными переменными.
В заключение, модели играют важную роль в научном исследовании, представляя явления и процессы в упрощенной и понятной форме. Они позволяют ученым анализировать, предсказывать, объяснять и обучать, что помогает развитию науки и прогрессу человечества.
Важность измерений для моделей
Измерения являются неотъемлемой частью создания и оценки моделей. Они позволяют получить количественные данные о явлениях и процессах, которые модель описывает. Измерения помогают выявить закономерности и взаимосвязи между различными переменными, а также установить значимые параметры модели.
Одним из основных преимуществ измерений является возможность получения объективных данных. Измерения позволяют исключить субъективные предположения и оценки, а основываться на фактах и конкретных числах. Это делает модели более точными и достоверными.
Измерения также помогают оценить качество модели и ее пригодность для решения задач. По результатам измерений можно сравнить прогнозную модель с фактическими данными и понять, насколько хорошо модель предсказывает будущие события. Это важно для принятия обоснованных решений и планирования деятельности.
Кроме того, измерения позволяют установить значимые параметры модели. Параметры модели это числовые значения, которые определяют ее характеристики и свойства. Измерения позволяют определить эти значения и использовать их для анализа модели и прогнозирования ее поведения.
Измерения также помогают выявлять ошибки и неточности в моделях. По результатам измерений можно оценить точность моделей и выявить возможные проблемы. Если результаты измерений не совпадают с ожидаемыми значениями, это может указывать на несоответствие модели действительности или наличие ошибок в ее построении.
Таким образом, измерения играют важную роль в создании и оценке моделей. Они позволяют получить объективные данные, оценить качество модели, установить значимые параметры и выявить ошибки. Благодаря измерениям модели становятся более точными, достоверными и полезными для решения различных задач.
Виды параметров моделей
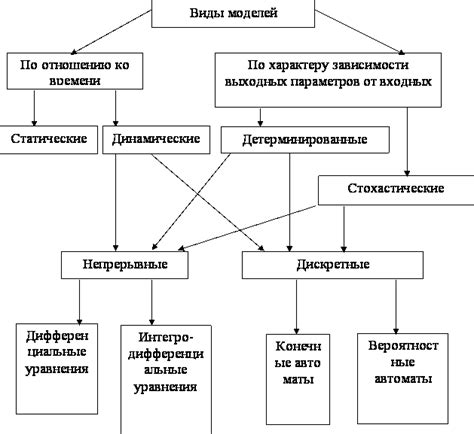
При построении и анализе моделей в науке и технике активно используются различные параметры, которые служат для определения свойств модели и ее поведения. В данном разделе рассмотрим основные виды параметров моделей.
- Геометрические параметры - это параметры, описывающие геометрическую форму модели. Например, длина, ширина, высота, радиус и т.д. Такие параметры могут быть важными при моделировании объектов, в которых геометрия играет важную роль, например, в архитектуре или механике.
- Физические параметры - это параметры, описывающие физические свойства моделируемого объекта. Например, масса, плотность, коэффициент трения и т.д. Физические параметры необходимы для моделирования физических систем, таких как движение тел или процессы теплообмена.
- Технические параметры - это параметры, описывающие технические характеристики модели. Например, мощность, скорость, производительность и т.д. Технические параметры важны при моделировании технических систем и устройств, таких как двигатели, электрические схемы и т.д.
- Экономические параметры - это параметры, описывающие экономические характеристики моделируемого процесса или объекта. Например, стоимость, прибыль, затраты и т.д. Экономические параметры играют важную роль при экономическом моделировании и оценке эффективности проектов.
Имея достаточно информации о различных параметрах моделей, исследователь или инженер может более точно определить их свойства, поведение и использование. Кроме того, параметры моделей позволяют проводить сравнительный анализ различных моделей и выбирать наиболее соответствующие конкретным задачам.
Как измерять параметры моделей
Измерение параметров моделей является важной частью машинного обучения и статистического моделирования. Эти параметры определяются с помощью различных методов и могут использоваться для оценки качества моделей, проверки гипотез и принятия решений.
Оценка параметров моделей
Измерение параметров моделей основано на оценке их значений с использованием доступных данных. Это может быть сделано с помощью различных методов, таких как метод наименьших квадратов или максимального правдоподобия. Цель состоит в том, чтобы найти такие значения параметров, которые наилучшим образом соответствуют данным.
Качество моделей
Измерение параметров моделей позволяет оценить их качество. Например, в задаче регрессии параметры модели могут использоваться для оценки точности предсказания. Чем ближе значения предсказания к истинным значениям, тем лучше модель работает.
Проверка гипотез
Измерение параметров моделей также может быть использовано для проверки гипотез. Например, предположим, что модель предсказывает вероятность события. Измерение параметров может позволить узнать, является ли разность между вероятностью, предсказанной моделью, и реальной вероятностью статистически значимой.
Принятие решений
Измерение параметров моделей также может помочь в принятии решений. Например, в задаче классификации модель может предсказать, принадлежит ли объект к определенному классу или нет. Измерение параметров модели может помочь в оценке вероятности принадлежности объекта к различным классам и, следовательно, в принятии решения о его классификации.
Особенности измерения временных параметров

Временные параметры являются важной характеристикой моделей, которая позволяет оценить их скорость выполнения и эффективность работы. Измерение временных параметров позволяет выявить узкие места в алгоритмах и оптимизировать процессы.
Однако измерение временных параметров может быть нетривиальной задачей, так как существуют ряд особенностей, которые нужно учитывать:
- Зависимость от аппаратных и программных характеристик системы. Время выполнения модели может изменяться в зависимости от мощности процессора, объема оперативной памяти, наличия других активных процессов и т.д.
- Случайные факторы. Время выполнения модели может подвергаться влиянию случайных факторов, таких как сетевая задержка, нагрузка на сервер и другие внешние условия.
- Порядок выполнения операций. Временные параметры могут зависеть от порядка выполнения операций. Например, в некоторых алгоритмах время выполнения может быть существенно различным при разном порядке обработки данных.
Для более точного измерения временных параметров рекомендуется использовать статистические методы, которые позволяют получить более надежные результаты. Например, можно выполнить несколько запусков модели и усреднить полученные значения, чтобы учесть случайные факторы и получить более устойчивую оценку времени выполнения.
Осознание и учет указанных особенностей позволяет более корректно измерять временные параметры моделей и получать более достоверные результаты, что является важным условием для правильной оценки и дальнейшей оптимизации процессов.
Сложности измерения пространственных параметров
Модели, используемые в научных исследованиях и инженерии, часто включают в себя описание объектов пространственных параметров. Это могут быть размеры, расстояния, площади, объемы и другие характеристики, связанные с геометрическими свойствами объектов.
Однако измерение пространственных параметров может столкнуться со множеством сложностей, связанных с точностью, доступностью и способом измерения. Вот некоторые из основных сложностей, с которыми сталкиваются исследователи:
- Измерение малых размеров: Измерение очень малых размеров, таких как нанометры или ангстремы, может быть крайне сложным и требовать использования специализированных приборов и методов. Существуют различные методы микроскопии и нанотехнологии, которые позволяют измерять такие параметры, но они могут быть дорогостоящими и требуют глубоких знаний и опыта для их использования.
- Ошибки измерения: При измерении пространственных параметров возникают различные ошибки, которые могут быть вызваны факторами, такими как неточность приборов, человеческий фактор, условия эксперимента и другие. Минимизация таких ошибок является важной задачей для получения достоверных и точных результатов.
- Инструменты и методы измерения: Для измерения пространственных параметров существует множество инструментов и методов. Выбор подходящего инструмента и метода зависит от конкретных требований и условий эксперимента. Некоторые из методов измерения включают лазерную дальномерную съемку, методы компьютерной томографии, использование специальных датчиков, оптических приборов и других технологий.
- Точность и повторяемость: Измерение пространственных параметров требует высокой точности и повторяемости. Точность определяет, насколько результаты измерения соответствуют истинным значениям параметров, а повторяемость показывает, насколько одинаковыми будут результаты измерений при повторном выполнении эксперимента.
- Сложность формы объектов: Некоторые объекты имеют сложную геометрическую форму, что может затруднить измерение и описание их пространственных параметров. В таких случаях может потребоваться использование математических методов и алгоритмов для аппроксимации и описания формы объектов.
В целом, измерение пространственных параметров является сложной задачей, требующей специализированных знаний, опыта и использования специальных инструментов и методов. Но благодаря постоянному развитию технологий и научным исследованиям, становится возможным получать все более точные и надежные данные о геометрических свойствах объектов.
Значимость мер и параметров для анализа моделей

Оценка и анализ моделей являются важным этапом в различных областях, таких как машинное обучение, статистика и эконометрика. Для достижения точных и надежных результатов необходимо определить и измерить различные меры и параметры моделей.
Одной из главных задач в анализе моделей является проверка их качества. Для этого используются различные метрики, которые позволяют оценить эффективность модели и сравнить ее с другими моделями. Например, популярной метрикой является средняя абсолютная ошибка (MAE), которая измеряет среднее отклонение прогнозов модели от фактических значений.
Другим важным аспектом анализа моделей является определение значимости различных параметров. Параметры модели представляют собой численные значения, которые определяют характеристики модели и влияют на ее поведение и прогнозы. Измерение значимости параметров позволяет понять, какие параметры вносят наибольший вклад в объяснение данных и прогнозирование.
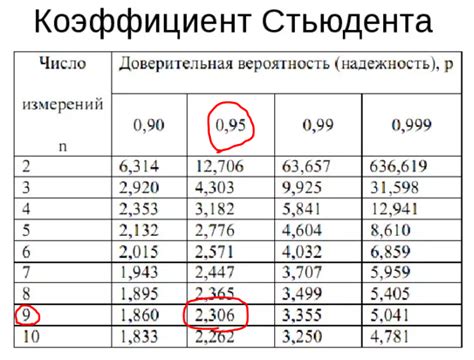
Существуют различные методы для измерения значимости параметров. Один из таких методов - t-статистика. Она позволяет оценить статистическую значимость параметра путем сравнения его значения с нулевой гипотезой. Если t-статистика превышает критическое значение, то это говорит о статистической значимости параметра и его важности для модели.
Помимо мер и параметров моделей, также важно учитывать контекст и особенности задачи, в которой используется модель. Не всегда самые точные модели являются наиболее удовлетворительными для задачи. Нередко требуется найти оптимальный баланс между точностью и интерпретируемостью модели.
Итак, измерение и оценка мер и параметров моделей играют важную роль в анализе и понимании их эффективности. Это позволяет выбрать наиболее подходящую модель для задачи и понять, какие параметры вносят наибольший вклад. Использование правильных мер и параметров поможет достичь более надежных результатов и принять обоснованные решения на основе моделирования данных.
Влияние точности измерений на результаты моделей
Точность измерений является важным фактором, который может оказывать значительное влияние на результаты моделей. В процессе создания и обучения моделей используются различные статистические методы и алгоритмы, которые требуют точных данных для достижения правильных результатов.
Неточные измерения могут привести к искажению параметров модели и неверному предсказанию. В идеальном случае, мы предполагаем, что имеем полный контроль над измерениями и что ошибки измерений отсутствуют. Однако, на практике точность измерений никогда не может быть идеальной.
Ошибки измерений могут быть вызваны различными факторами, такими как шумы, погрешности датчиков, амбиентные условия и множество других. Даже небольшие погрешности могут вызвать заметные изменения в результатах модели, поэтому необходимо учитывать точность измерений при использовании моделей и анализе данных.
Для учета точности измерений можно использовать различные методы, такие как взвешивание данных, учет погрешностей, корректировка результатов и т.д. В зависимости от задачи и специфики данных выбирается подходящий метод учета точности. Важно помнить, что учет точности измерений является неотъемлемой частью процесса моделирования и анализа данных.
При работе с моделями и анализе данных необходимо предоставить адекватную точность измерений для получения правильных результатов. Детальное понимание точности измерений и ее влияния на результаты моделей позволяет сделать более достоверные и обоснованные выводы на основе анализа данных.
Точность измерений играет ключевую роль в научном и инженерном исследовании. Она позволяет определить, насколько точно мы можем измерить и предсказать значения параметров, что является основой для принятия обоснованных решений и разработки эффективных моделей.
Критическое обсуждение измерений и параметров моделей
Измерения и параметры моделей играют важную роль в научных и технических исследованиях. Они позволяют описать и изучить объекты и явления, а также сравнить различные модели и оценить их точность и полезность.
Однако, несмотря на свою важность, измерения и параметры моделей не всегда являются точными и достоверными. Измерения могут быть загрязнены случайной ошибкой или систематической погрешностью, что приводит к неточным и неправильным результатам. Кроме того, параметры моделей могут быть субъективными и зависеть от предположений и приближений, что также влияет на точность и надежность модели.
Важно также учитывать, что не все измерения и параметры моделей являются равнозначными. Некоторые измерения могут быть более точными и информативными, чем другие. Например, измерение с использованием высокоточного прибора будет более точным, чем измерение с простым инструментом. Также параметры модели могут иметь различную значимость и степень влияния на результаты и выводы.
Критическое обсуждение измерений и параметров моделей требует внимания и осторожности. Важно учитывать все возможные источники погрешностей и субъективности, а также проводить проверку и подтверждение результатов с помощью независимых методов и данных.
Также следует помнить, что измерения и параметры моделей могут быть ограничены и неполными. Некоторые характеристики и влияющие факторы могут быть сложными для измерения или вообще недоступными. В таких случаях необходимо быть осторожными при интерпретации и использовании результатов модели.
В итоге, критическое обсуждение измерений и параметров моделей является неотъемлемой частью научного исследования. Оно помогает нам понять ограничения и возможности модели, а также достичь более точных и надежных результатов.
Вопрос-ответ
Какие меры и параметры используются для измерения моделей?
Для измерения моделей используются различные меры и параметры, в зависимости от целей и задач исследования. Некоторые из них включают в себя статистические меры, такие как среднеквадратическое отклонение и коэффициент корреляции, а также экономические меры, такие как прирост доходов или снижение затрат. Кроме того, в модельном анализе используются различные параметры, такие как коэффициенты регрессии и показатели качества моделей, которые позволяют оценивать и сравнивать эффективность моделей.
Зачем нужны меры и параметры моделей?
Меры и параметры моделей необходимы для оценки эффективности моделей и сравнения их между собой. Они позволяют исследователям получить численные результаты, на основе которых можно делать выводы о работе моделей и их применимости к конкретным задачам. Кроме того, меры и параметры моделей могут служить основой для принятия решений и разработки стратегий в различных областях, таких как экономика, финансы, маркетинг, и т.д.
Как измеряется эффективность моделей?
Эффективность моделей может быть измерена с помощью различных мер и параметров. Например, в экономике и финансах используется показатель прироста доходов или снижения затрат в результате применения модели. В статистике применяются меры точности, такие как коэффициент корреляции или среднеквадратическое отклонение. В маркетинге можно использовать параметры регрессии для оценки влияния различных факторов на целевую переменную. Определение эффективности моделей в каждом конкретном случае зависит от поставленных задач и целей исследования.
Какие меры и параметры используются для оценки качества моделей?
Для оценки качества моделей используются различные меры и параметры. Некоторые из них включают в себя коэффициент детерминации, который показывает, какая часть изменчивости зависимой переменной объясняется моделью, а также среднеквадратическую ошибку, которая показывает, насколько сильно модель отклоняется от фактических данных. Кроме того, для оценки качества моделей могут использоваться различные статистические тесты, такие как t-тесты или анализ дисперсии, которые позволяют провести сравнение моделей и проверить их значимость.