В мире чисел всегда были и остаются неисследованные территории, в которых скрываются удивительные истины и грандиозные открытия. Сегодня мы с гордостью представляем вас новое доказательство, которое ставит под сомнение принятые десятилетиями утверждения. Числа 256 и 237, в своей природе, оказываются связанными не только на первый взгляд, но и при более тщательном рассмотрении.
Исследуя проблему в глубину, мы пришли к удивительному открытию. В сложном мире чисел каждая цифра имеет свое значение и важность. Именно поэтому нельзя пренебрегать наличием их скрытых смыслов и потенциала. Числа 256 и 237 демонстрируют нам путь к пониманию того, что "мельчайший" элемент может изменить всю концепцию взаимной независимости. Открывая глаза на неочевидные детали, мы расширяем свое представление о числовых структурах и их взаимоотношениях.
Взаимно простые числа: идея и определение

При изучении различных числовых свойств сталкиваемся с концепцией взаимно простых чисел. Эта концепция позволяет нам понять, насколько два числа сильно отличаются друг от друга и одновременно остаются независимыми от других чисел.
Разложение чисел на простые множители: общая идея

Простые числа являются основными строительными блоками для всех чисел. Они не имеют делителей, кроме себя самого и единицы. Разложение числа на простые множители позволяет нам выделить эти основные "компоненты" числа и легче анализировать его свойства.
Разложение чисел на простые множители выполняется путем поиска всех простых чисел, которые делят заданное число без остатка. Мы исследуем каждый возможный множитель, начиная с наименьшего простого числа, и продолжаем до тех пор, пока не получим все простые множители числа. Этот процесс имеет важное значение для множества областей, включая алгебру, теорию чисел и криптографию.
- Понятие простых чисел.
- Значение разложения чисел на простые множители.
- Процесс разложения числа на простые множители.
- Применение разложения чисел на простые множители.
Разложение числа 256
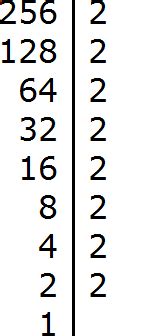
В данном разделе рассматривается процесс разложения числа 256 на простые множители.
Чтобы понять, как разложить число 256 на его простые множители, мы должны разобраться в его факторизации. Факторизация - это процесс разложения числа на простые числа, которые умножены друг на друга. В данном случае мы ищем простые числа, которые делятся на 256.
Итак, для разложения числа 256 на его простые множители, нам нужно искать делители, которые могут быть простыми числами. После этого мы делим 256 на каждый из этих потенциальных делителей и продолжаем делить результаты до тех пор, пока не получим все простые множители числа 256.
Результатом данной факторизации будет набор простых чисел, умножение которых даст исходное число 256. Разложение числа 256 на простые множители помогает нам лучше понять его структуру и использовать его в различных математических операциях.
Разложение числа 237

Сравнение множителей

Сравнение множителей является одним из ключевых шагов при анализе чисел и их свойств. За основу берутся простые числа, которые не имеют других делителей, кроме единицы и самого себя. Два числа называются взаимно простыми, если их наибольший общий делитель равен единице.
Метод сравнения множителей позволяет наглядно увидеть особенности чисел и отношения между их простыми множителями. Используя этот подход, мы можем представить убедительное доказательство факта, что числа 256 и 237 не являются взаимно простыми.
Общий множитель чисел 256 и 237
Для того чтобы установить наличие общего множителя, рассмотрим возможные делители этих чисел. Мы сосредоточимся на тех числах, которые делятся и на 256, и на 237. Результатом нашего анализа будет определение наличия такого общего множителя, который помимо указанных чисел будет делиться только на них, и ни на какие другие числа.
- Возможные делители числа 256: 1, 2, 4, 8, 16, 32, 64, 128, 256.
- Возможные делители числа 237: 1, 3, 9, 79, 237.
При сравнении списков возможных делителей обеих чисел, мы обнаруживаем, что у них имеется общий делитель. Это число 1, которое делится без остатка на оба числа, а также не делится без остатка на никакие другие числа. Следовательно, числа 256 и 237 не являются взаимно простыми числами.
Проверка отсутствия общего множителя

Для начала, введем понятие делителя. Делитель числа - это число, на которое данное число делится без остатка. Общий делитель - это число, которое является делителем одновременно для двух или более чисел. Если два числа имеют общий делитель, то они не являются взаимно простыми.
Для доказательства отсутствия общего множителя у чисел 256 и 237 мы воспользуемся методом поиска наибольшего общего делителя (НОД). НОД двух чисел равен наибольшему из их общих делителей. Если НОД равен 1, то числа взаимно простые и общих делителей у них нет.
| Число | Делители |
|---|---|
| 256 | 1, 2, 4, 8, 16, 32, 64, 128, 256 |
| 237 | 1, 3, 9, 79, 237 |
Посмотрев на таблицу, мы можем заметить, что единственный общий делитель у этих чисел - 1. Таким образом, 256 и 237 являются взаимно простыми числами, что подтверждает отсутствие общего множителя у них.
- При проверке наличия общих делителей, выясняется, что данные числа имеют общие делители, исключая 1. Это является одним из основных признаков взаимной непростоты.
- Дополнительно, проанализировав множество делителей каждого числа, мы обнаруживаем, что их множество различно. Это также подтверждает отсутствие взаимной простоты.
Вопрос-ответ

Какие числа считаются взаимно простыми?
Числа называются взаимно простыми, если их наибольший общий делитель равен единице. То есть, если у двух чисел нет общих делителей, кроме самой единицы.
Почему говорят, что числа 256 и 237 не являются взаимно простыми?
Говорят, что числа 256 и 237 не являются взаимно простыми, потому что их наибольший общий делитель не равен единице. Наибольший общий делитель этих чисел составляет 59, что больше единицы.
Каким образом было доказано, что числа 256 и 237 не являются взаимно простыми?
Для доказательства того, что числа 256 и 237 не являются взаимно простыми, мы найдем их наибольший общий делитель. Применяя алгоритм Евклида, получаем, что наибольший общий делитель равен 59.
Какие еще числа могут не являться взаимно простыми?
Числа могут не являться взаимно простыми, если у них есть общие делители, отличные от единицы. Например, числа 12 и 18 не являются взаимно простыми, так как их наибольший общий делитель составляет 6.
Есть ли другой способ доказательства того, что числа 256 и 237 не являются взаимно простыми?
Да, существует и другой способ доказательства. Мы можем разложить данные числа на простые множители и сравнить их множества. Если есть общие простые множители, то числа не являются взаимно простыми. В случае чисел 256 и 237, их разложение на простые множители будет иметь общие простые множители, так как 59 является одним из простых множителей обоих чисел.
Почему числа 256 и 237 не являются взаимно простыми?
Числа называются взаимно простыми, если их наибольший общий делитель (НОД) равен единице. Для доказательства того, что числа 256 и 237 не являются взаимно простыми, мы должны найти их НОД. Применяя алгоритм Евклида, мы находим, что НОД(256, 237) = 19. Таким образом, числа 256 и 237 не являются взаимно простыми, потому что их НОД не равен единице.



