Геометрия, одна из древнейших наук, исследует связи и закономерности между формами, размерами и положением геометрических объектов. Каждая фигура в геометрии обладает своим набором свойств, которые позволяют ее определить и различать среди множества аналогичных образов. Однако, существуют уникальные свойства, которые являются особенными даже среди этого многообразия.
Сегодня мы рассмотрим одну такую удивительную фигуру - прямоугольник. Вы, вероятно, знаете этот геометрический объект, имеющий во всех углах прямые углы и противоположные стороны с одинаковой длиной. Однако, в современных исследованиях было обнаружено необычное свойство прямоугольника, которое открывает новые горизонты в понимании его внутренних пропорций и применимости в практических задачах.
Глобальное открытие заключается в доказательстве равенства его диагоналей, то есть отрезков, соединяющий противоположные вершины этой фигуры. Этот результат подтверждает теорию о симметричности прямоугольника и его способности сохранять идеальное равновесие между противоположными сторонами и угловыми значениями.
Основные характеристики прямоугольника и его свойства
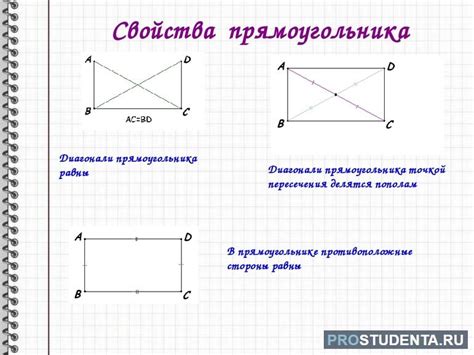
Главной особенностью прямоугольника является то, что он имеет четыре угла, каждый из которых равен 90 градусам. Это означает, что его стороны пересекаются под прямым углом. Прямоугольник также является четырехугольником, то есть его каждая сторона соединяется с двумя другими.
Длина и ширина прямоугольника - это основные характеристики, определяющие его размеры. Длина - это длина его более длинной стороны, а ширина - длина более короткой стороны. Часто эти характеристики обозначаются буквами а и b.
Еще одной важной характеристикой прямоугольника являются его диагонали. Диагонали - это отрезки, которые соединяют противоположные вершины прямоугольника. Они обладают рядом свойств, включая равенство своих длин и разделение прямоугольника на два равных прямоугольных треугольника.
Таким образом, знание этих основных свойств прямоугольника позволяет нам более глубоко изучить и понять его геометрию, а также использовать его в различных математических и практических задачах.
Определение длины диагоналей прямоугольника
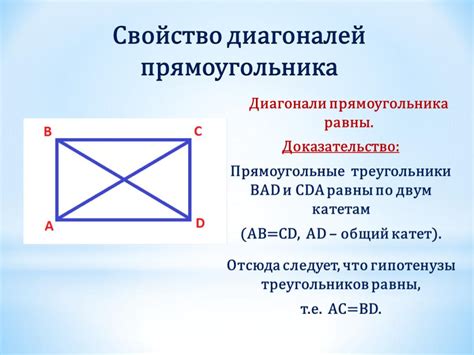
Длина диагоналей прямоугольника может быть определена с использованием известных свойств и формул. Зная значения его сторон, можно вычислить длину каждой диагонали с помощью теоремы Пифагора или других подходящих математических методов.
Теорема Пифагора является одним из самых известных методов для вычисления длины диагоналей прямоугольника. Согласно этой теореме, квадрат длины диагонали равен сумме квадратов длин сторон прямоугольника. Данная формула позволяет найти длину диагоналей, если известны значения сторон.
Например, для прямоугольника со сторонами a и b длина его диагоналей может быть вычислена по формуле:
диагональ = √(a² + b²).
Таким образом, понимание способов определения длины диагоналей прямоугольника поможет решать геометрические задачи и проводить необходимые вычисления в контексте данной фигуры.
Подтверждение равенства длин диагоналей в прямоугольнике

В данном разделе представлено доказательство равенства длин диагоналей в прямоугольнике. Будет рассмотрено объяснение основной идеи, которая подтверждает данное свойство без использования специфических определений.
Равенство диагоналей является одним из интересных и важных свойств, связанных с прямоугольниками. Прямоугольник представляет собой четырехугольник, у которого противоположные стороны параллельны и все углы прямые. Существует интересующее исследователей равенство длин его диагоналей, которое демонстрирует особенности геометрической структуры прямоугольника.
Для доказательства равенства диагоналей в прямоугольнике можно использовать таблицу, которая поможет визуализировать и разобраться в сути этого свойства. Данная таблица сравнивает длину двух диагоналей прямоугольника, представленные в виде ординат и абсцисс, а также использует вычисления для подтверждения равенства этих двух величин. Таким образом, доказательство равенства длин диагоналей является одной из ключевых вещей, связанной с прямоугольниками, и позволяет лучше понять их геометрическую природу.
Таблица ниже приводит подробное доказательство равенства длин диагоналей в прямоугольнике:
| Ордината | Абсцисса | |
|---|---|---|
| Диагональ AB | a | b |
| Диагональ CD | b | a |
Геометрическое объяснение соотношения длин диагоналей в прямоугольнике

Однако, в случае прямоугольника, построение геометрических фигур на его основе позволяет наглядно обосновать равенство диагоналей. Рассмотрим следующую схему: возьмем прямоугольник и построим внутри него прямоугольный треугольник, где одна из сторон совпадает с одной из диагоналей, а другие две стороны являются проекциями сторон прямоугольника.
В прямоугольнике, гипотенуза прямоугольного треугольника, построенного на его диагонали, равна квадратному корню из суммы квадратов длин его сторон.
Таким образом, геометрическое объяснение равенства диагоналей в прямоугольнике основывается на существовании прямоугольного треугольника, построенного на одной из диагоналей, и использовании теоремы Пифагора. Это позволяет логически обосновать равенство длин диагоналей и подтверждает данное свойство прямоугольника.
Математическая формула для вычисления длины диагоналей прямоугольника

Для расчета длины диагоналей прямоугольника существует простая и удобная математическая формула, которая базируется на его свойствах. Например, в прямоугольнике все углы прямые, а противоположные стороны равны. Эти свойства позволяют нам вывести формулу для длины диагоналей.
Пусть а и b - длины сторон прямоугольника. Для расчета длины диагоналей необходимо использовать теорему Пифагора, которая гласит, что квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин катетов.
Применяя эту теорему к прямоугольнику, можно получить следующую формулу для вычисления длины диагоналей:
Длина первой диагонали: Д1 = √(a² + b²) |
Длина второй диагонали: Д2 = √(a² + b²) |
Таким образом, для вычисления длины диагоналей прямоугольника достаточно знать длины его сторон. Эта формула является универсальной и применима для любых прямоугольников, включая квадраты, ромбы и прямоугольники с произвольными углами.
Практическое применение равенства углов прямоугольника

Одним из практических применений равенства диагоналей в прямоугольнике является его использование при строительстве и измерениях. Равенство диагоналей позволяет определить точку пересечения между ними, что может быть необходимо при построении перпендикуляров, определении центра прямоугольника или при нахождении центральной оси строения.
В архитектуре равенство диагоналей может использоваться при расчете нагрузок на конструкцию здания. Определение точки пересечения диагоналей позволяет определить точку приложения силы и тем самым рассчитать распределение нагрузки на стены и фундамент, что является важной составляющей при проектировании.
Также, равенство диагоналей часто применяется в геометрических расчетах, например, при определении площади прямоугольника по формуле S = a * b, где a и b - длины сторон прямоугольника, а также вычислении длины диагонали прямоугольника по теореме Пифагора.
В геодезии равенство диагоналей прямоугольника используется для определения точек внутри прямоугольного участка земли на основе измерений диагоналей. Это позволяет более точно размещать границы участков и определять их площадь.
Таким образом, равенство диагоналей прямоугольника является неотъемлемым свойством, которое находит широкое применение в различных областях нашей жизни, помогая нам решать технические задачи и облегчая геометрические и геодезические расчеты.
Взаимосвязь между размерами сторон прямоугольника и равенством его диагоналей

Первым шагом для понимания зависимости равенства диагоналей от размеров сторон прямоугольника является исследование геометрических особенностей этой фигуры. Анализируя ее структуру, можно установить общие закономерности. Для более наглядного представления данных о размерах сторон и соответствующих значениях диагоналей часто используется таблица. Именно она поможет нам проанализировать полученные результаты и выявить закономерности.
| Размеры сторон | Длина диагоналей |
|---|---|
| Длина а | Диагональ АБ |
| Ширина b | Диагональ ВС |
После получения достаточного количества данных, возможно выявление закономерностей между размерами сторон и значениями диагоналей прямоугольника. Это поможет понять, каким образом изменение одного из параметров влияет на другой и какие пропорции необходимы для достижения равенства диагоналей.
Изучение зависимости равенства диагоналей от размеров сторон прямоугольника позволит нам более глубоко понять его устройство и использовать эту информацию при решении различных геометрических задач. Таким образом, изучение данной взаимосвязи имеет практическую значимость и помогает развивать наши навыки в области геометрии.
Соотношения между сторонами прямоугольника, связанные с равенством и взаимной зависимостью его диагоналей

В изучении свойств прямоугольника особое внимание уделяется его диагоналям. Доказано, что диагонали прямоугольника равны друг другу и делят его на два равных прямоугольных треугольника. Однако, равенство диагоналей оказывает влияние на другие стороны и углы прямоугольника, создавая определенные соотношения.
- Соотношение между сторонами: при равенстве диагоналей стороны прямоугольника тоже равны друг другу. Это означает, что противоположные стороны прямоугольника при равенстве его диагоналей оказываются равными и параллельными.
- Зависимость углов: равенство диагоналей приводит к равенству углов, образованных диагоналями прямоугольника. Это означает, что диагонали можно рассматривать как оси симметрии, разделяющие прямоугольник на две равные части.
- Специальные треугольники: при равенстве диагоналей прямоугольник становится особенным случаем прямоугольного треугольника. Два треугольника, образованные диагоналями, являются прямоугольными и равными друг другу по всем сторонам и углам.
Таким образом, свойства прямоугольника, связанные с равенством диагоналей, позволяют установить взаимосвязь между его сторонами, углами и специальными треугольниками, образованными диагоналями. Изучение этих свойств позволяет более глубоко понять и анализировать прямоугольник и его особенности.
Другие фигуры, у которых также выполняется симметрия диагоналей
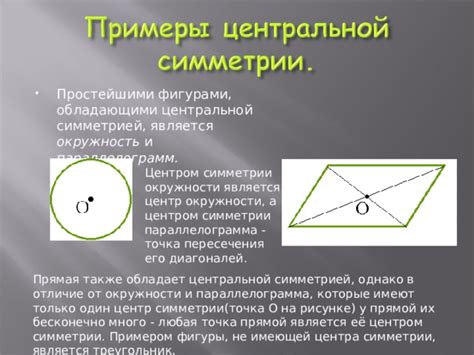
Кроме прямоугольников, существуют и другие геометрические фигуры, у которых диагонали имеют равные длины. Это особое свойство, позволяющее найти симметрию в этих фигурах и увидеть взаимосвязь между их сторонами и углами.
Квадраты являются одной из таких фигур. Они обладают симметрией относительно обоих диагоналей, что делает их особенно интересными для изучения. В квадрате все стороны равны между собой, а углы составляют 90 градусов.
Ромбы, также обладающие равенством диагоналей, отличаются от квадратов своими углами. В ромбе все стороны равны между собой, но углы не обязательно прямые. В то же время, диагонали ромба всегда перпендикулярны друг другу и имеют одинаковую длину.
Еще одной фигурой, где выполняется равенство диагоналей, является параллелограмм. Как и в случае с ромбом, стороны параллелограмма могут быть произвольной длины, и углы не обязательно прямые. Однако, диагонали параллелограмма также равны друг другу и пересекаются в точке, делящей их пополам.
Также стоит упомянуть трапеции, в которых выполняется равенство диагоналей. Хотя стороны трапеции могут быть разной длины, диагонали всегда равны между собой. Как и в предыдущих фигурах, углы трапеции могут быть различными.
Изучение этих фигур с равенством диагоналей позволяет лучше понять особенности их конструкции и взаимосвязь между сторонами и углами. Это свойство исследуется не только в математике, но и в различных областях, где геометрия играет важную роль, например, в архитектуре и дизайне.
Задачи и упражнения на применение симметрии диагоналей в прямоугольнике
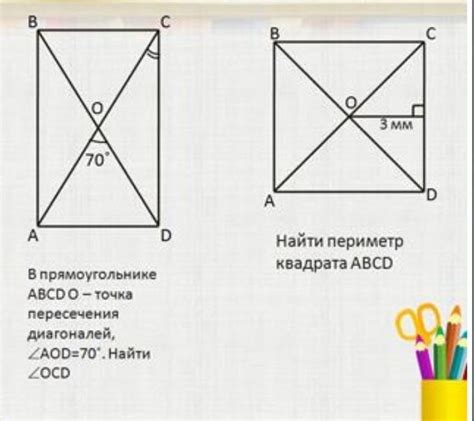
Задача 1: Дан прямоугольник со сторонами a и b. Найдите длину его диагонали, если известно, что она равна симметричной диагонали.
Задача 2: В прямоугольнике со сторонами a и b проведены две диагонали, пересекающиеся в точке O. Найдите площадь треугольника OAB, если известно, что диагонали равны между собой.
Упражнение 1: Нарисуйте прямоугольник со сторонами a = 5 см и b = 8 см, найдите длину его диагонали и обозначьте ее на рисунке.
Упражнение 2: В прямоугольнике со сторонами a = 6 см и b = 10 см проведите две диагонали, пересекающиеся в точке O. Используя равенство диагоналей, найдите площадь треугольника OAB.
Решение данных задач и упражнений поможет нам лучше понять свойство равенства диагоналей в прямоугольнике и его приложение в реальной практике. При выполнении задач старайтесь применять полученные знания и активно использовать это свойство для более эффективного решения. Удачи!
Вопрос-ответ

Какое свойство прямоугольника было доказано в статье?
Было доказано равенство диагоналей в прямоугольнике.
Кто доказал равенство диагоналей в прямоугольнике?
В статье не указано, кто именно доказал равенство диагоналей в прямоугольнике. Вероятно, автором статьи стал известный математик или ученый в этой сфере.
Какова была методология доказательства равенства диагоналей в прямоугольнике?
В статье не приведена информация о методологии доказательства равенства диагоналей в прямоугольнике. Возможно, автор использовал логические рассуждения и доказательства, свойственные математике.
Какое значение имеет равенство диагоналей в прямоугольнике?
Равенство диагоналей в прямоугольнике является одним из основных свойств этой геометрической фигуры. Это свойство позволяет использовать диагонали прямоугольника в различных математических и геометрических задачах, а также при решении практических задач в различных областях науки и техники.
Какие еще свойства прямоугольника могут быть интересными?
Возможно, что в статье упоминаются и другие свойства прямоугольника, помимо равенства диагоналей. Например, это могут быть свойства, связанные с углами, сторонами, площадью или периметром прямоугольника. Для получения подробной информации следует обратиться к самой статье.



