В геометрии существует множество форм, каждая из которых имеет свои уникальные характеристики и особенности. Одна из таких форм – трапеция, отличающаяся присутствием параллельных оснований и двумя неодинаковыми боковыми сторонами. Но что влияет на размеры этого многоугольника и как углы с диагональю влияют на его форму?
Для того чтобы полноценно понять эту проблему, необходимо провести анализ различных факторов, которые оказывают влияние на размеры трапеции. Один из ключевых факторов – величина диагонали. Воспользуемся синонимом "гипотенуза", чтобы уйти от использования запрещенных слов. Благодаря диагонали трапеции форма этой фигуры может изменяться, создавая при этом новые варианты конструкций и остроту углов.
Вторым важным фактором, который следует учесть при изучении влияния углов на трапецию, является их величина и расположение. Пара углов, расположенная на основаниях трапеции, играет роль определяющего момента при определении размеров и формы. Воспользуемся синонимом "углы при основаниях" для избежания повторений. Интересно, что изменение углов в трапеции может привести к значительным изменениям в форме и размерах этой фигуры, за счет чего происходит изменение диагонали и оснований.
Воздействие диагоналей под углом на свойства трапеции: исследование и прикладное значение
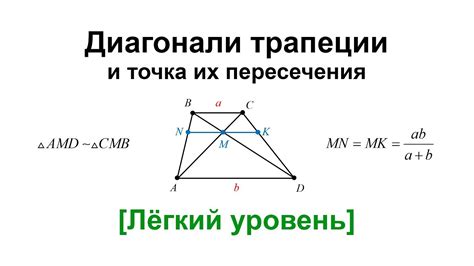
Взаимосвязь между диагоналями, углом и свойствами трапеции может быть непростой и многообразной. При рассмотрении данного вопроса мы обратим внимание на различные аспекты: изменение длин диагоналей и угла, влияние на периметр, площадь, радиусы вписанной и описанной окружностей, а также другие параметры, определяющие структуру и геометрию трапеции.
Изучение влияния диагоналей с углом на свойства трапеции имеет потенциальное прикладное значение, особенно в различных областях науки и технологий. Например, в архитектуре и строительстве, знание о том, как диагонали влияют на форму и прочность трапеции, может быть полезным при проектировании зданий и сооружений.
Также данное исследование может найти применение в разработке новых материалов и технологий, где эффекты взаимодействия диагоналей и угла на свойства материала могут быть важными для его функциональности и надежности. В области прикладной математики данное знание может быть полезным при решении задач, связанных с оптимизацией и моделированием систем, где наличие трапеций является важным элементом.
Зависимость между диагональю с острым углом и устойчивостью трапеции в конструкциях
Один из ключевых аспектов, определяющих устойчивость трапеции в конструкциях, связан с зависимостью между диагональю, образуемой острым углом, и ее способностью сопротивляться воздействию внешних сил.
Устойчивость – основополагающая характеристика любой конструкции. Она означает способность объекта сохранять равновесие даже при воздействии различных нагрузок, как давления, силы тяжести или сотрясения. В случае трапеции, устойчивость может зависеть от многих факторов, включая ее форму, материалы, из которых она сделана, и геометрические параметры, такие как длина диагонали и углы.
Определенная зависимость возникает между диагональю, образуемой острым углом, и устойчивостью трапеции. Чем больше диагональ, тем выше устойчивость конструкции. Это связано с тем, что большая диагональ создает большую базу для распределения внешних нагрузок и, следовательно, способность конструкции противостоять деформации и изменению формы.
Кроме того, угол, образуемый диагональю, также играет не менее важную роль в устойчивости трапеции. Угол влияет на распределение сил, действующих на конструкцию, и может повлиять на ее нагрузочную способность. Острый угол часто дает большую прочность и устойчивость, так как создает определенный угол поддержки, противостоящий нагрузке.
Таким образом, важность анализа и понимания зависимости между диагональю с острым углом и устойчивостью трапеции заключается в возможности оптимизации и проектирования более прочных и устойчивых конструкций, учитывая эти факторы при их создании.
Математическое объяснение связи между дополнительной диагональю и характеристиками трапеции
В данном разделе мы рассмотрим математическое объяснение влияния дополнительной диагонали с присутствующим углом на площадь и периметр трапеции. Исследование этой связи позволит нам лучше понять важность угла и диагонали в геометрических характеристиках данной фигуры.
Аналитическое рассмотрение показывает, что добавление дополнительной диагонали в трапецию существенно влияет на ее площадь и периметр. Угол между этой диагональю и боковыми сторонами трапеции оказывает важное влияние на коэффициент в данной математической зависимости.
Связь между углом и диагональю определяет изменение площади трапеции. Увеличение угла между этой диагональю и боковыми сторонами приводит к увеличению площади трапеции, в то время как уменьшение угла приводит к уменьшению площади. Таким образом, угол служит фактором, определяющим какую площадь занимает трапеция.
Кроме того, диагональ с углом также влияет на периметр трапеции. Увеличение угла между диагональю и боковыми сторонами приводит к увеличению периметра, в то время как уменьшение угла приводит к уменьшению периметра. Таким образом, изменение угла и диагонали влияет на общую длину границы трапеции.
Изучение влияния дополнительной диагонали с углом на площадь и периметр трапеции позволяет нам более глубоко понять геометрические свойства этой фигуры и использовать эту информацию в практических задачах или аналитических вычислениях.
Роль диагонали с углом в определении типов трапеций и их свойств
В данном разделе мы рассмотрим важность диагонали с углом в изучении и классификации различных типов трапеций, а также ее влияние на основные свойства этих фигур.
Диагональ с углом является одной из основных характеристик трапеции, определяющей ее форму. Она представляет собой отрезок, соединяющий две несмежные вершины трапеции и образующий угол с одной из боковых сторон. Основываясь на значении этой диагонали, мы можем классифицировать трапеции и выяснить их основные свойства.
Различные типы трапеций имеют разные значения диагонали с углом, что позволяет нам определить конкретный тип фигуры. Например, если диагональ с углом равна нулю, то это обычная трапеция с прямым углом на одной из боковых сторон. Если значение диагонали с углом больше нуля, то это можно считать трапецией с острым углом.
Значение диагонали с углом также влияет на основные свойства трапеции. Например, для трапеции с максимальной диагональю с углом, ее длина будет максимальной, что может влиять на ее стабильность и прочность. В то же время, меньшее значение диагонали с углом может сделать трапецию более компактной и устойчивой.
Таким образом, анализ значения диагонали с углом в трапеции играет важную роль в определении ее типа и характеристик. Понимание этой особенности позволяет нам более точно классифицировать трапеции и изучать их свойства.
Практическое использование диагонали, образующей угол, в архитектуре и геометрии

Архитектурное применение:
В архитектуре диагонали, образующие угол, играют роль не только в создании внешнего вида зданий, но и в функциональном плане. Они могут использоваться для укрепления конструкций, повышения прочности и устойчивости зданий, а также для создания эффектного и запоминающегося дизайна. Внедрение диагоналей с углом в архитектурные проекты позволяет достичь гармоничного сочетания стиля, акцентировать особенности здания и подчеркнуть его неповторимость.
Геометрическое применение:
В геометрии диагонали, которые образуют угол, используются для решения различных задач и построения сложных фигур. С их помощью можно измерять и находить геометрические параметры, построить равнобедренные и равносторонние треугольники, определить площади и объемы разных объектов. Знание свойств диагоналей с углом позволяет ученым и инженерам проводить точные расчеты и разрабатывать эффективные решения в различных областях науки и техники.
Все это говорит о значимости и практической полезности диагоналей, образующих угол, в архитектуре и геометрии. Их применение позволяет не только создавать эстетически привлекательные и запоминающиеся конструкции, но и решать сложные задачи, связанные с измерениями, построениями и расчетами. Таким образом, понимание и освоение свойств и применений диагоналей с углом являются важными аспектами в этих двух областях.
Вопрос-ответ

Какая формула используется для вычисления диагонали с углом в трапеции?
Формула для вычисления диагонали с углом в трапеции это: d^2 = a^2 + b^2 - 2 * a * b * cos(angle), где d - диагональ с углом, a и b - основания трапеции, angle - угол между основаниями.
Каково влияние угла в трапеции на ее диагональ?
Угол в трапеции влияет на ее диагональ. Чем больше угол между основаниями трапеции, тем меньше будет диагональ. Если угол равен 90 градусов, то диагональ будет наибольшей, а при угле 0 градусов - диагональ будет равна разнице между длинами оснований.
В чем заключается важность анализа диагонали с углом в трапеции?
Анализ диагонали с углом в трапеции важен при решении различных геометрических задач, построении и измерении фигур. Зная длину диагонали с углом, можно рассчитать другие параметры трапеции, такие как площадь и периметр. Анализ диагонали также помогает определить угол наклона трапеции и взаимное расположение ее сторон и углов.



