В мире геометрии, где каждый угол и каждая линия имеют свои законы и связи, существуют некоторые скрытые истины, которые ожидают своих поклонников иследователей. И одной из таких является взаимосвязь между вписанными треугольником и окружностью.
Как лишь взглянуть на окружность, сложно догадаться о ее скрытых свойствах и возможностях, которые она предлагает нам. Однако по мере погружения в изучение геометрии, мы начинаем замечать, что внутри окружности можно создать особый треугольник, имеющий некоторые зацепления и связи с самой окружностью.
Но что если этот вписанный треугольник оказывается не просто связан окружностью, но и обладает интересным свойством - является прямоугольным? Ведь именно эта идея возбуждает нашу любознательность и подталкивает нас к поиску эффективных методов для доказательства о его правом угле. Сегодня мы рассмотрим несколько из таких методов, которые позволяют убедиться в прямоугольности вписанного треугольника и разгадать тайны, которые прячутся под его азимутом.
Идея вписанного треугольника и основные свойства
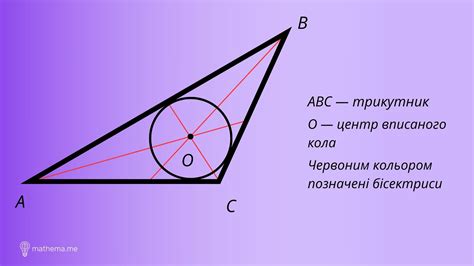
В этом разделе мы рассмотрим концепцию вписанного треугольника, его основные свойства и связь с окружностью.
Вписанный треугольник – это треугольник, все вершины которого лежат на окружности.
Одно из важных свойств вписанного треугольника – теорема о центральном угле. Она утверждает, что угол, образуемый хордой и соответствующей дугой на окружности, равен половине измерения дуги.
Другим важным свойством вписанного треугольника является теорема о прямом угле. Она утверждает, что если один из углов треугольника является прямым, то треугольник вписан в окружность.
Свойство касательной к окружности, проведенной из вершины вписанного треугольника, также является характерным для данного типа треугольника. Касательная к окружности является перпендикулярной радиусу, проведенному в точку касания. Это свойство позволяет находить множество углов, используя тангенс и секущую вписанную окружность.
- Вписанный треугольник – треугольник, все вершины которого лежат на окружности.
- Теорема о центральном угле – угол, образуемый хордой и соответствующей дугой на окружности, равен половине измерения дуги.
- Теорема о прямом угле – если один из углов треугольника является прямым, то треугольник вписан в окружность.
- Свойство касательной – касательная к окружности, проведенная из вершины вписанного треугольника, является перпендикулярной радиусу, проведенному в точку касания.
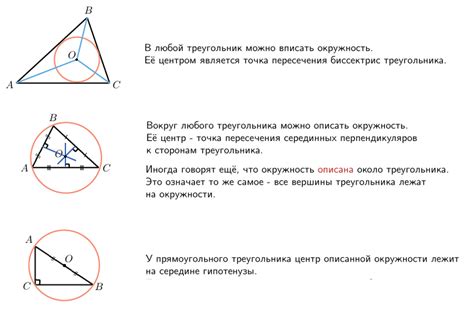
Определение и основные свойства треугольников, вписанных в окружность
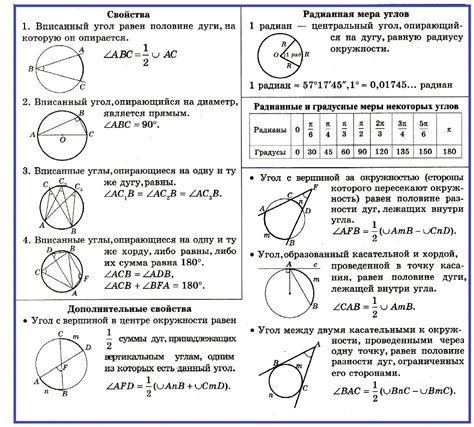
В данном разделе рассматривается понятие и ключевые характеристики треугольников, которые могут быть вписаны в окружность. Окружности представляют собой геометрические фигуры, состоящие из точек, равноудаленных от фиксированной точки, называемой центром окружности. Треугольник, вписанный в окружность, определяется тремя вершинами, каждая из которых лежит на окружности.
Первое основное свойство вписанного треугольника, известное также как теорема о центральном угле, заключается в том, что любой центральный угол, образованный двумя хордами, равен половине его пересекающего дугу угла. Другими словами, угол, охватываемый двумя хордами, равен половине угла, опирающегося на ту же дугу.
Второе основное свойство вписанного треугольника, известное как теорема о хордах, утверждает, что если два треугольника вписаны в одну и ту же окружность и имеют общую хорду, то отношения их площадей равны отношению длин соответствующих сторон.
Третье основное свойство вписанного треугольника состоит в том, что сумма углов треугольника, вписанного в окружность, равняется 180 градусам. Это следует из того, что угол, опирающийся на дугу, равен половине меры этой дуги.
Знание и понимание основных характеристик вписанных треугольников является важным для доказательства их свойств. Подробное изучение этих свойств может помочь в решении разнообразных задач, связанных с треугольниками, вписанными в окружность, и использовании их в практических приложениях геометрии.
Три способа определить прямоугольность треугольника, описанного вокруг окружности
- Использование теоремы о величине угла, образованного диаметром и хордой окружности
- Применение свойства ортогонально вписанной окружности и её хорды
- Использование теоремы синусов для треугольника, описанного вокруг окружности
Первый метод основан на теореме о величине угла, образованного диаметром и хордой окружности. Если треугольник такой, что одна из его сторон является диаметром окружности, а другая сторона - хордой, то угол, образованный этими сторонами, является прямым. Это свойство можно использовать для определения прямоугольности треугольника, описанного вокруг окружности.
Второй метод основан на свойстве ортогонально вписанной окружности и её хорды. Если окружность описана вокруг треугольника и одна из хорд этой окружности является высотой или медианой этого треугольника, то треугольник будет прямоугольным. Это свойство позволяет достаточно просто определить прямоугольность треугольника, описанного вокруг окружности.
Третий метод основан на теореме синусов для треугольника, описанного вокруг окружности. Если в треугольнике, описанном вокруг окружности, угол при одном из вершин прямой, то это означает, что противоположная ему сторона - диаметр окружности. Пользуясь этим свойством, можно определить прямоугольность треугольника, описанного вокруг окружности.
Выберите один из вышеописанных методов, максимально удобный в вашей конкретной ситуации, чтобы доказать прямоугольность треугольника, описанного вокруг окружности.
Методы для определения вписанности треугольника в окружность
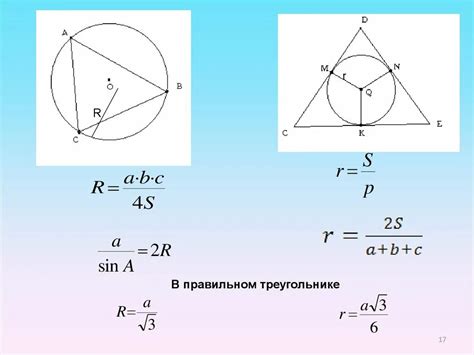
Ключевой аспект изучения треугольников, которые удовлетворяют особому свойству, связанному с окружностью, предлагает несколько методов, позволяющих определить, вписан ли треугольник в окружность. Эти методы основаны на различных характеристиках и свойствах, которые связаны с понятием вписанности и освещают его с разных сторон.
Отношение между вписанными в окружность треугольниками и их прямоугольными свойствами

В этом разделе мы рассмотрим связь между треугольниками, вписанными в окружность, и их прямоугольными свойствами. Определение прямоугольного треугольника, входящего в окружность, имеет особое значение при изучении этой темы. Мы исследуем интересные сокращения и последствия, которые возникают при наличии соответствующих условий.
Наши рассмотрения начнем с определения прямоугольного треугольника, который содержит в себе особое отношение с окружностью. Исследуемый треугольник, при правильных условиях, будет обладать следующими свойствами: одна из его сторон будет служить диаметром окружности, а противоположный ей угол будет прямым. Будем называть такой треугольник "вписанным" и "прямоугольным".
Для понимания и использования данного отношения, изучим несколько важных результатов. Если треугольник является вписанным и прямоугольным, то его стороны будут обладать определенными соотношениями между собой. С помощью подобия треугольников и теоремы Пифагора, мы сможем вывести формулы, позволяющие найти длины сторон вписанного прямоугольного треугольника.
- Рассмотрим соотношение сторон треугольника, вписанного в окружность, с учетом его прямоугольности.
- Применим теорему Пифагора к вписанному прямоугольному треугольнику и получим формулы, связывающие его стороны.
- Исследуем свойства и сокращения, проистекающие из соотношений сторон вписанного прямоугольного треугольника.
С помощью данных методов и их применения к конкретным примерам, мы можем эффективно определить прямоугольные треугольники, вписанные в окружность, а также изучить их связь с окружностью. Упрощение данной задачи позволяет нам избежать излишней сложности и эффективно использовать полученные результаты в дальнейших исследованиях и применениях.
Свойства прямоугольных треугольников и их взаимосвязь с окружностью
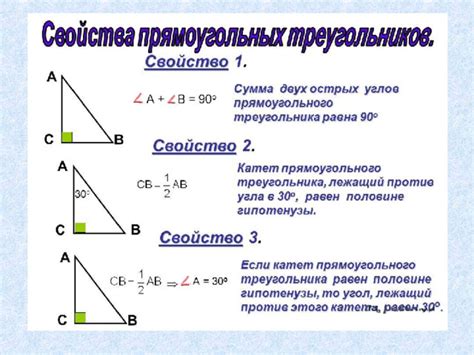
Здесь мы рассмотрим основные свойства прямоугольных треугольников и их связь с окружностью. Они представляют собой особый класс треугольников, в которых один из углов равен 90 градусам. Благодаря этому свойству, прямоугольные треугольники обладают рядом интересных характеристик, связанных как с их сторонами, так и с вписанной окружностью.
Во-первых, прямоугольный треугольник является основой для понятия тригонона. Тригонон - это прямоугольный треугольник со сторонами, образующими арифметическую прогрессию. Интересно отметить, что вписанная окружность тригонона касается его сторон в точках деления их отрезками, образующими арифметическую прогрессию. Это свойство можно использовать для нахождения радиуса вписанной окружности по формуле Рауса.
Во-вторых, прямоугольный треугольник также является основой для построения прямоугольной системы координат, где один из катетов служит осью Х, а другой - осью Y. Это облегчает анализ геометрических и алгебраических свойств прямоугольных треугольников с помощью координатных методов.
Кроме того, прямоугольный треугольник имеет важную геометрическую связь с окружностью - теорему Пифагора. Согласно этой теореме, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Это свойство имеет глубокие корни в геометрии и находит применение в решении различных задач.
- Прямоугольный треугольник является особой формой треугольника со свойствами, не присущими другим типам треугольников.
- Вписанная окружность тригонона касается его сторон в точках деления их отрезками, образующими арифметическую прогрессию.
- Прямоугольный треугольник используется в построении прямоугольной системы координат.
- Прямоугольный треугольник связан с окружностью через теорему Пифагора, которая находит применение во многих математических и физических задачах.
Геометрический подход к проверке включения треугольника в круг
Один из таких способов основан на теореме о перпендикулярности биссектрисы угла треугольника к соответствующей стороне. Если биссектриса является высотой (перпендикуляром) треугольника и проходит через его вершину, то треугольник будет вписанным в окружность.
Другим способом является использование угловой меры центрального угла, образованного окружностью и сторонами треугольника. Если мера этого угла равна 90 градусам, то треугольник будет прямоугольным и, следовательно, вписанным в окружность.
Геометрический подход: доказательство вписанности через фигуры и углы

Использование геометрического подхода при доказательстве вписанности треугольника в окружность позволяет проиллюстрировать эту концепцию с помощью фигур и углов. Благодаря этому подходу, мы можем более наглядно представить процесс и увидеть, почему треугольник вписан в окружность.
При использовании геометрического подхода мы рассматриваем взаимосвязь между сторонами и углами треугольника, а также его отношение с окружностью. Наблюдая за различными фигурами, включающими треугольник и окружность, мы можем увидеть определенные закономерности и связи между элементами конструкции.
Один из наглядных способов доказательства вписанности треугольника в окружность - это установление связи между центральным углом треугольника и накрест лежащими углами, образованными между сторонами треугольника и окружностями. Здесь мы можем использовать фигуры, такие как хорда и дуги, чтобы проиллюстрировать существующие углы и их отношения между собой.
Более сложные геометрические рассуждения также могут быть применены для доказательства вписанности треугольника в окружность. Например, мы можем использовать свойства равенства углов, соотношения между центральным и накрест лежащими углами и другие понятия геометрии, чтобы подтвердить наше утверждение.
Использование геометрического подхода для доказательства вписанности треугольника в окружность не только помогает увидеть связь и взаимодействие между этими двумя фигурами, но и дает возможность понять, почему треугольник является прямоугольным. Этот подход предоставляет нам интуитивное понимание того, какое должно быть взаимное расположение сторон и углов, чтобы треугольник был вписан в окружность и имел прямой угол.
Алгебраический подход к доказательству вписанности треугольника в окружность
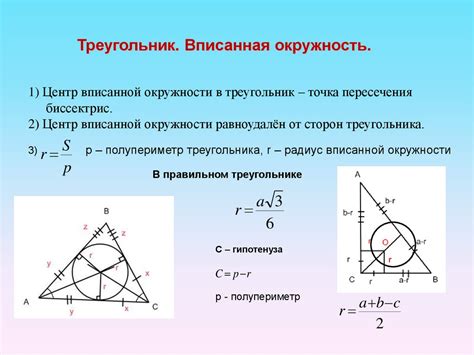
Основной идеей алгебраического подхода является представление окружности в виде уравнения с включением координат точек, лежащих на окружности. Аналогично, треугольник представляется в виде уравнений для каждой из его сторон. Далее, используя систему алгебраических уравнений, мы можем найти их общее решение, которое будет описывать случай, когда треугольник вписан в окружность.
Для доказательства вписанности треугольника в окружность при помощи алгебраического подхода, нам необходимо решить систему уравнений трех прямых, задающих стороны треугольника, и уравнение окружности. Это можно сделать с помощью метода подстановки или метода Крамера, позволяющих найти значения координат точек пересечения сторон треугольника и окружности.
- Представим треугольник в виде трех уравнений прямых, задающих его стороны.
- Представим окружность в виде уравнения с использованием координат точек, лежащих на окружности.
- Составим систему уравнений, включающую уравнения трех сторон треугольника и уравнение окружности.
- Решим систему алгебраических уравнений, используя метод подстановки или метод Крамера.
- Если решение системы позволяет найти значения координат точек пересечения сторон треугольника и окружности, то треугольник является вписанным в окружность.
Алгебраический подход к доказательству вписанности треугольника в окружность предоставляет нам эффективный способ проверки этого свойства без использования геометрических измерений и свойств. Этот метод особенно полезен в случаях, когда геометрическое доказательство является сложным или неочевидным.
Вопрос-ответ

Как доказать, что треугольник вписанный в окружность прямоугольный?
Существует несколько простых и эффективных методов для доказательства прямоугольности треугольника, вписанного в окружность. Один из таких методов основан на теореме о центральном угле. Если треугольник ABC вписан в окружность O, и угол ABC - прямой угол, то треугольник ABC является прямоугольным. Для доказательства этого факта необходимо доказать, что угол в центре, соответствующий этому дуге AB, равен 180°. Другим простым методом является использование теоремы о проекции диагонали на диаметр окружности. Если диагональ BC треугольника ABC является высотой, а диагональ AC является диаметром, то треугольник ABC будет прямоугольным. Также можно использовать теорему о равенстве пар противоположных углов для прямоугольного треугольника, вписанного в окружность.
Как использовать теорему о центральном угле для доказательства прямоугольности треугольника, вписанного в окружность?
Для использования теоремы о центральном угле в доказательстве прямоугольности треугольника, вписанного в окружность, необходимо найти угол в центре, соответствующий прямому углу треугольника. Для этого нужно измерить дугу, на которую опирается данный угол, и убедиться, что эта дуга равна 180°. Если эта дуга равна 180°, то треугольник является прямоугольным.
Как применить теорему о проекции диагонали для доказательства прямоугольности треугольника, вписанного в окружность?
Для применения теоремы о проекции диагонали для доказательства прямоугольности треугольника, вписанного в окружность, нужно убедиться, что одна из диагоналей треугольника является высотой, а другая диагональ является диаметром окружности. Если это условие выполняется, то треугольник будет прямоугольным.
Как доказать, что треугольник вписанный в окружность прямоугольный?
Существует несколько методов доказательства прямоугольности вписанного треугольника. Один из эффективных методов основан на свойстве теоремы о прямом угле в полукруге. Если угол между хордой треугольника и диаметром, проходящим через его вершину, равен 90 градусам, то треугольник вписанный в окружность является прямоугольным.



