Построение и измерение треугольников являются важными навыками для математиков и инженеров всех уровней. Одним из самых важных заданий в работе с треугольниками является нахождение и измерение биссектрисы, линии, разделяющей угол на две равные части.
Безусловно, существует много способов нахождения биссектрисы треугольника, но в данной статье мы рассмотрим один из самых простых и эффективных - использование лишь циркуля и линейки. Этот метод, который основан на базовых геометрических принципах, позволяет точно найти биссектрису треугольника без использования сложной техники.
В начале мы рассмотрим, как правильно построить треугольник с помощью циркуля и линейки, а затем перейдем к основным шагам для измерения биссектрисы. Каждый из этих шагов будет подробно объяснен и показан на примерах, что позволит вам легко и успешно применять этот метод в своей работе.
Пошаговое руководство по нахождению оси симметрии треугольника

- Выберите любую сторону треугольника и обозначьте ее с помощью точки A и B.
- На стороне AB используя циркуль, отметьте точку между A и B.
- Берите линейку и проведите прямую линию через новую отмеченную точку и вершину треугольника C. Обозначьте эту точку как D.
- Теперь проведите прямую линию, соединяющую точку D и середину противолежащей стороны треугольника. Обозначьте эту точку как E.
- Точка E является точкой пересечения оси симметрии треугольника. Проведите линию, соединяющую точку E и вершину треугольника B. Итак, теперь у вас есть ось симметрии, или биссектриса, треугольника.
Следуя этим шагам, вы сможете легко определить ось симметрии треугольника. Биссектриса треугольника является важным инструментом для изучения геометрии и нахождения значений связанных с треугольником, таких как углы и площадь.
Определение биссектрисы треугольника и ее свойства
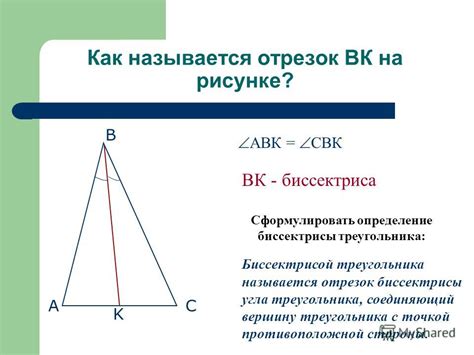
Биссектриса треугольника имеет несколько значимых свойств. Во-первых, точка пересечения биссектрис углов треугольника является центром вписанной окружности. Это означает, что радиус окружности, описанной вокруг этого треугольника, равен половине длины биссектрисы. Во-вторых, биссектрисы трех углов треугольника пересекаются в одной точке, которая называется точкой пересечения биссектрис. Эта точка делит каждую биссектрису в отношении длин смежных сторон. Наконец, биссектрисы треугольника создают шесть сегментов, которые имеют пропорциональные соотношения в соответствии с теоремой о биссектрисах.
Теперь, когда мы понимаем общую идею биссектрисы треугольника и ее свойства, давайте перейдем к более детальному рассмотрению этой темы и способам определения биссектрисы с использованием циркуля и линейки.
Необходимые инструменты: циркуль и линейка

Циркуль - это инструмент, состоящий из двух ног, соединенных петлей, при помощи которых можно регулировать расстояние между ними. Он позволяет нам проводить окружности с заданным радиусом, а также делать точные отметки на плоскости.
Линейка - это прямоугольный инструмент с делениями, которые позволяют нам измерять длины отрезков и проводить прямые линии. Линейка бывает разной длины и выполнена из разных материалов, но важно, чтобы она была прочной и имела четкие деления, чтобы проводить точные измерения.
Циркуль и линейка являются основными инструментами геометрии и позволяют нам проводить точные измерения и выполнить необходимые построения для нахождения биссектрисы треугольника. Их правильное использование и понимание особенностей работы с ними являются важными навыками для каждого, кто увлекается геометрией или стремится выполнить точные вычисления.
Шаг 1: Определение точки пересечения двух сторон треугольника

Шаг 2: Использование циркуля для построения дуги из найденной точки

Как только мы находимся в найденной точке на одной из сторон треугольника, мы берем циркуль и устанавливаем одну его ножку на данную точку. Затем, с помощью второй ножки циркуля, мы проводим дугу, создавая дуговидную линию от данной точки в сторону противоположной стороны треугольника.
Важно помнить, что при использовании циркуля необходимо уметь поддерживать постоянный радиус дуги. Это позволит нам построить точку пересечения на стороне треугольника, расположенной напротив точки, с которой мы начали строить дугу.
После построения дуги, нам остается провести прямую линию от найденной точки пересечения с одной из сторон треугольника до противоположного угла. Таким образом, мы определяем вторую часть биссектрисы треугольника, что приближает нас к нашей конечной цели.
Шаг 3: Обнаружение точки пересечения дуги с третьей стороной треугольника

В этом разделе мы рассмотрим процесс определения второй точки пересечения созданной дуги с третьей стороной треугольника. Это важный шаг в нахождении биссектрисы треугольника и позволяет определить точку, где дуга пересекает третью сторону. Наше руководство поможет вам выполнять эту задачу с помощью циркуля и линейки.
- Возьмите циркуль и отметьте на третьей стороне треугольника точку, которая будет первой точкой пересечения дуги.
- Затем, используя линейку, проведите прямую линию, проходящую через эту точку и перпендикулярно к третьей стороне треугольника.
- Определите середину этой линии и отметьте ее.
- Возьмите циркуль и установите его центр в этой отмеченной точке.
- Настройте радиус циркуля так, чтобы он достигал точки, где дуга пересекает другую сторону треугольника.
- Затем, не меняя радиус циркуля, проведите дугу от первой точки пересечения до второй точки пересечения на третьей стороне.
- Эта дуга пересекает третью сторону треугольника во второй точке пересечения, которую мы ищем. Отметьте эту точку с помощью циркуля.
Теперь, после определения обеих точек пересечения дуги с третьей стороной треугольника, вы можете продолжить процесс нахождения биссектрисы треугольника и достичь окончательного результата.
Шаг 4: Построение линии-биссектрисы сквозь образовавшиеся точки на плоскости

После того как мы нашли точки пересечения двух биссектрис, пришло время соединить их, чтобы получить саму биссектрису треугольника. Для этого нам понадобятся циркуль и линейка.
Возьмите циркуль и проведите окружность с центром в одной из найденных точек пересечения. Радиус этой окружности должен быть достаточно большим, чтобы она пересекала вторую точку пересечения и образовывала дугу на плоскости.
Затем, переместив циркуль на другую найденную точку пересечения, отметьте точку, где дуга окружности пересекается с линией, соединяющей две точки пересечения. Эта точка будет являться третьей точкой на биссектрисе треугольника.
Нарисуйте прямую через первую точку пересечения и новую точку, полученную на предыдущем шаге. Эта прямая будет являться линией-биссектрисой и делит угол треугольника на две равные части.
Повторите те же шаги для двух других углов треугольника, чтобы найти и нарисовать остальные две биссектрисы. После завершения этого шага у вас будет построена биссектриса каждого угла треугольника, помогая лучше понять его геометрию и свойства.
Проверка правильности построения биссектрисы с использованием свойств

В данном разделе мы рассмотрим методы проверки правильности построения биссектрисы треугольника с помощью известных свойств и синтаксических элементов геометрии.
Во-первых, одним из важных свойств биссектрисы является то, что она делит противоположную сторону треугольника на две сегменты, пропорциональные двум другим сторонам. Для проверки правильности можно измерить отношение длин этих сегментов и сравнить их с соответствующими значениями, полученными из изначального треугольника. Если отношения совпадут, значит, биссектриса построена корректно.
Во-вторых, биссектриса является перпендикуляром к стороне треугольника и проходит через точку деления этой стороны на две части, пропорциональные двум другим сторонам. Для проверки правильности построения можно провести перпендикуляр из точки деления на противоположную сторону и убедиться, что этот перпендикуляр пересекает противоположный угол и делит его пополам.
Также можно использовать свойство равенства трех углов, чтобы проверить правильность построения биссектрисы. Для этого нужно замерить каждый из углов, образованных биссектрисой и сторонами треугольника, и убедиться, что они равны.
Важно помнить, что эти методы являются проверочными и не дают гарантии абсолютной правильности построения биссектрисы. Для этого необходимо использовать точные математические методы и инструменты, такие как угломер или компьютерные программы для геометрической конструкции.
Вопрос-ответ

Какие инструменты следует использовать для нахождения биссектрисы треугольника?
Для нахождения биссектрисы треугольника понадобятся циркуль и линейка. Циркуль используется для проведения окружностей, а линейка поможет провести стороны треугольника и провести линию от вершины треугольника до точки пересечения окружностей. Эти простые инструменты позволят точно найти биссектрису треугольника.
Можно ли найти биссектрису треугольника без использования циркуля и линейки?
Найти биссектрису треугольника без использования циркуля и линейки, как правило, невозможно. Циркуль позволяет проводить окружности с заданным радиусом, что пригодно в данном случае. Линейка же необходима для проведения сторон треугольника и линии от вершины до точки пересечения окружностей. Отсутствие одного из этих инструментов затруднит и усложнит нахождение биссектрисы треугольника.
Можно ли использовать другие инструменты для нахождения биссектрисы треугольника?
Да, помимо циркуля и линейки, существуют и другие инструменты, которые можно использовать для нахождения биссектрисы треугольника. Например, существуют специальные инструменты для измерения углов, такие как градусник или полукруглый транспортир. Эти инструменты позволяют точно измерять углы треугольника и находить их биссектрисы. Кроме того, в некоторых случаях можно использовать геометрические теоремы и свойства треугольников для нахождения биссектрисы без использования дополнительных инструментов.
Какой метод нахождения биссектрисы треугольника самый точный?
Все методы нахождения биссектрисы треугольника могут быть точными, если правильно использовать инструменты и следовать геометрическим правилам. Однако использование специальных инструментов, таких как градусник или транспортир, может дать более точные результаты, поскольку эти инструменты позволяют измерять углы с большей точностью. Но с другой стороны, правила и методы, использующие только циркуль и линейку, могут быть достаточно точными при правильном применении. Все зависит от тщательности измерений и выполнения геометрических конструкций.



