Как найти диагональ квадрата через сторону без лишних усилий - простой и эффективный способ, который поможет вам справиться даже с самыми сложными задачами

В современном мире математика стала неотъемлемой частью нашей повседневной жизни. Каждый из нас, даже не задумываясь, использует ее принципы и формулы, решая множество задач. Однако, существуют особые случаи, где требуется нахождение диагонали квадрата по его стороне, и здесь может возникнуть некоторая сложность.

Необходимость в знании этого простого и надежного алгоритма возникает при решении различных задач геометрии или при построении объектов, где точное определение диагонали квадрата становится критически важным. Предлагаем вам уникальный способ, который сможет помочь в этом вопросе без лишних усилий и временных затрат.

В этой статье мы рассмотрим, как буквально в несколько шагов определить диагональ квадрата, используя только знания основных математических принципов. Используя этот метод, вы сможете точно и быстро решать различные задачи, связанные с квадратами и их геометрическими характеристиками.

Вычисление противоположной стороны квадрата через уже известную

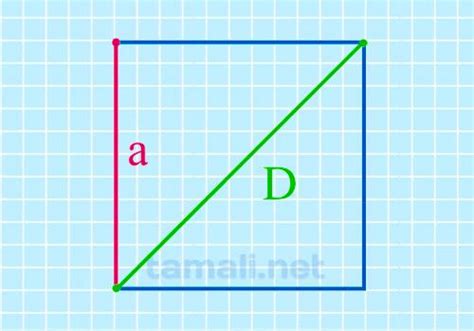
В данном разделе мы рассмотрим метод определения значения противоположной стороны квадрата, исходя из известной стороны. Это позволит нам упростить процесс вычисления и получить нужный результат без излишней сложности.

Для начала рассмотрим некоторые основные понятия, которые понадобятся нам в дальнейшем. Квадрат – это геометрическая фигура, обладающая четырьмя равными сторонами. Диагональ квадрата, также являющаяся его стороной, соединяет две противоположные вершины и образует прямой угол. Мы будем рассматривать квадрат со стороной a, где a – известное значение, из которого мы хотим узнать противоположную сторону.

Известная сторона квадрата:	a
Противоположная сторона:	b

Для определения противоположной стороны квадрата мы можем воспользоваться теоремой Пифагора, которая связывает длины сторон прямоугольного треугольника. Рассмотрим эту теорему для нашей задачи:

Гипотенуза:	c
Катет 1 (известная сторона):	a
Катет 2 (противоположная сторона):	b

Теорема Пифагора гласит: квадрат длины гипотенузы равен сумме квадратов длин катетов. В нашем случае это будет выглядеть так:

c² = a² + b²

Учитывая, что в квадрате все стороны равны, мы можем записать a² = b²:

c² = 2a²

Далее, чтобы найти значение противоположной стороны квадрата, достаточно взять квадратный корень из полученного значения:

b = √(2a²)

Итак, мы получили простую формулу для нахождения противоположной стороны квадрата через уже известную сторону. Отличительной особенностью данного метода является его простота и эффективность, поскольку он основан на применении известной теоремы Пифагора и не требует сложных вычислений.

Теоретическое понимание процесса нахождения длины диагонали квадрата проходит через изучение связи между его стороной и этой величиной.

В данном разделе мы сосредоточимся на абстрактной стороне проблемы, основу которой составляет понимание математических связей и закономерностей.

Рассмотрим понятие квадрата, как геометрической формы, обладающей особыми свойствами. У геометрической фигуры отсутствуют атрибуты, связанные с практическими применениями, и она рассматривается в чисто абстрактном плане. В случае квадрата, его форма определяется симметричностью сторон и углами.

Важным элементом при решении задачи нахождения диагонали является понимание связи между стороной и диагональю. Здесь нам может помочь интуитивное понимание, но также необходимо отталкиваться от математических законов, таких как теорема Пифагора.

Таким образом, теоретический аспект включает в себя изучение основных свойств квадрата, анализ и понимание математических закономерностей и использование их для нахождения длины диагонали через сторону.

Применение в реальной жизни

Результаты научных исследований по нахождению диагонали квадрата через сторону находят свое практическое применение в различных сферах деятельности. Новые методы и алгоритмы, основанные на этом принципе, позволяют решать задачи эффективно и с высокой точностью.

Одним из примеров практического применения этой концепции является строительство. Благодаря способности находить диагональ квадрата, используя только известные данные о его стороне, проектировщики и инженеры могут оптимизировать расчеты и проверять правильность строительных конструкций.

В архитектуре это позволяет точно определить необходимую длину и углы прямоугольника для создания идеального квадрата, что способствует гармоничности и эстетичности зданий и сооружений.
В гражданском строительстве данный способ нахождения диагонали используется для проверки квадратности элементов фундамента и стен, что обеспечивает устойчивость и долговечность зданий.
В проектировании дорожных сетей такая техника применяется для определения правильной ширины и длины перекрестков, гарантируя безопасность и удобство движения транспорта.

Кроме строительства, нахождение диагонали квадрата через сторону имеет реальное значение в образовании и научных исследованиях. Математики и физики применяют данное знание для разработки сложных моделей и определения свойств различных физических явлений.

В геометрии эта концепция используется для нахождения площади и периметра квадрата, что является основой для решения задач и формул в школьной программе.
В физике это позволяет определить длину диагонали в прямоугольном тело и вычислить различные значения, такие как площадь поверхности и объем.
В исследованиях в области компьютерной графики этот метод нахождения диагонали квадрата позволяет создавать реалистичные 3D-модели и анимации, обеспечивая правильные пропорции и визуальную точность.

Таким образом, практическое применение нахождения диагонали квадрата через сторону охватывает различные области деятельности, внося положительные изменения и улучшения в процессы проектирования, изучения и практического применения математических и физических понятий.

Примеры вычислений

Для более наглядного понимания и использования метода определения диагонали квадрата на основе известной стороны, рассмотрим несколько примеров расчетов.

Пример 1: Допустим, нам известна сторона квадрата, равная "а". Чтобы найти диагональ, достаточно умножить значение "а" на корень квадратный из 2. Таким образом, диагональ D будет равна D = а * √2.

Пример 2: Предположим, что задана сторона квадрата, обозначаемая как "х". Чтобы определить длину диагонали в этом случае, нужно умножить значение "х" на √2, что приведет к формуле D = х * √2.

Пример 3: Пусть наша исходная задача состоит в определении длины диагонали, зная сторону квадрата, обозначаемую как "с". Для этого просто нужно умножить значение "с" на корень квадратный из 2, что приведет к формуле D = с * √2.

Приведенные примеры позволяют легко и быстро определить длину диагонали квадрата, используя значение известной стороны и математическую формулу. Этот простой метод эффективен и может быть использован в решении различных задач, связанных с квадратами.

Вопрос-ответ