Погружение в мир геометрии и математики зачастую сопровождается волнением и замешательством. Одним из понятий, которое нужно освоить для успешного путешествия по этой области знаний, является косинус угла. Многим может показаться, что это сложное понятие, однако на самом деле, расчет и понимание косинуса угла доступны каждому.
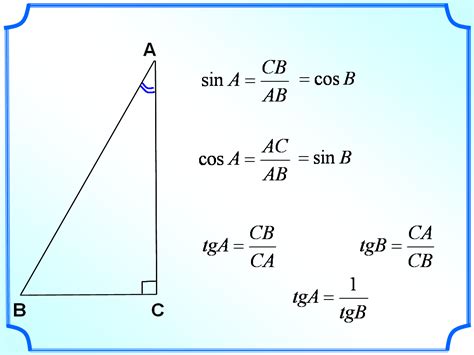
Косинус – это геометрическая функция, позволяющая узнать отношение длины прилежащего катета к гипотенузе прямоугольного треугольника. Он найдет свое применение в различных областях науки и техники, от физики до компьютерной графики. Данная функция позволяет определить угол между различными объектами, исследовать траектории движения и расстояния в пространстве.
Методы расчета косинуса угла варьируются от простых и интуитивно понятных до более сложных и точных. От выбора конкретного метода будет зависеть удобство и точность расчета. Некоторые из методов требуют использования сложных формул и табличных данных, в то время как другие могут быть легко выполнены с помощью простейших вычислительных инструментов. В данной статье мы рассмотрим несколько простых и понятных способов расчета косинуса угла, которые будут полезны как начинающим, так и более опытным математикам.
Косинус угла и его связь с треугольником

Косинус угла определяется как отношение длины прилежащего катета (стороны) треугольника к длине гипотенузы (главной стороны), когда угол помещен между ними. Другими словами, косинус угла показывает, насколько близко или далеко расположена точка на гипотенузе от начала координат.
Когда мы говорим о треугольнике и косинусе угла, мы подразумеваем, что у нас есть три стороны треугольника и один из углов. Косинус этого угла можно рассчитать, используя формулу, которая основана на соотношении длин сторон треугольника.
Важно отметить, что косинус угла может принимать значение от -1 до 1. Значение -1 соответствует ситуации, когда точка находится на противоположном конце гипотенузы, а значение 1 означает, что точка находится в начале гипотенузы. Значение 0 соответствует точке на середине гипотенузы.
Зная значение косинуса угла и длину гипотенузы треугольника, мы можем определить длину прилежащего катета или стороны треугольника. Это полезно при решении задач, связанных с измерением и построением треугольников, а также в научных и инженерных расчетах.
Геометрическое представление значения угла с использованием косинуса

Угол, как геометрическая величина, может быть представлен в виде отрезка на координатной плоскости. При этом, косинус угла представляет собой отношение длины прилежащего катета к гипотенузе прямоугольного треугольника, образованного этим углом. Геометрическая интерпретация косинуса угла позволяет нам одновременно изучать и анализировать как углы, так и их значения на числовой шкале.
Важно отметить, что значение косинуса угла может изменяться в пределах от -1 до 1. Значение косинуса угла равно 1, когда угол равен 0°, и равно -1, когда угол равен 180° или π (пи) радиан. Значения косинуса угла между 0° и 180° определяются в зависимости от величины угла и его положения в осях координатной плоскости. Таким образом, геометрическое представление косинуса угла является ключевым инструментом для анализа углов и их свойств.
Геометрическое представление косинуса угла открывает перед нами множество возможностей в изучении углов и их влияния на различные аспекты геометрии и других научных дисциплин. Понимание и правильное использование геометрических понятий, таких как косинус угла, является важной составляющей в освоении математики и решении практических задач.
Трегонометрическое представление косинуса угла
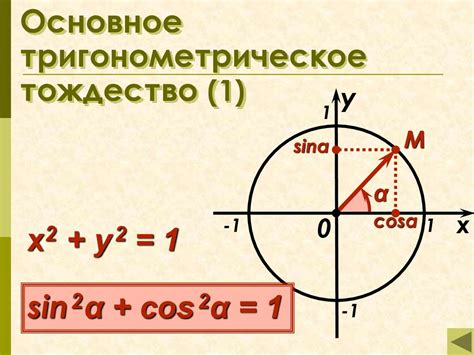
Основная идея трегонометрического представления косинуса заключается в том, что для каждого угла можно найти соответствующую точку на окружности единичного радиуса, в так называемой единичной окружности. Эта точка принадлежит прилегающему катету прямоугольного треугольника, образованного углом и радиусом окружности.
- Единичная окружность - окружность с радиусом 1, расположенная в координатной плоскости.
- Угол - мера поворота радиуса окружности от начального положения до запрашиваемого угла.
- Катет - отрезок, соединяющий центр окружности с точкой, находящейся на окружности и противолежащей углу.
Таким образом, трегонометрическое представление косинуса угла позволяет нам выразить косинус угла через координаты точки на единичной окружности и радиус окружности.
Значение косинуса угла через таблицу: удобный и простой способ расчета

Таблица косинусов углов представляет собой предварительно подсчитанные значения косинусов для различных углов. В такой таблице можно найти косинус каждого угла, просто подставив его значение.
Преимущества использования таблицы косинусов очевидны: нет необходимости выполнять сложные вычисления, таблица облегчает процесс нахождения точного значения косинуса и позволяет сэкономить время при решении задач, требующих данный расчет. Кроме того, таблица визуально представляет зависимость изменения косинуса от значения угла, что помогает лучше понять суть этой тригонометрической функции.
Ниже представлен пример таблицы косинусов углов:
| Угол, градусы | Косинус угла |
|---|---|
| 0° | 1 |
| 30° | 0,866 |
| 45° | 0,707 |
| 60° | 0,5 |
| 90° | 0 |
Найдя нужный угол в таблице, можно сразу узнать значение косинуса без дополнительных вычислений. Помимо данного примера, существуют таблицы с более широким диапазоном углов, которые можно найти в учебниках или в Интернете.
Вычисление косинуса угла без использования таблиц

В данном разделе представлены простые способы вычисления значения косинуса угла без необходимости обращения к таблицам и сложных вычислительных методов. Вместо этого, мы рассмотрим методы, основанные на простых математических операциях и свойствах тригонометрических функций.
Один из самых простых способов вычисления косинуса угла - использовать соотношение между катетом и гипотенузой прямоугольного треугольника. Угол, косинус которого мы хотим найти, должен быть острый. Пусть a - катет, примыкающий к углу, и c - гипотенуза треугольника. Тогда косинус угла определяется как отношение длины катета к длине гипотенузы: cos(α) = a/c.
Если прямоугольный треугольник не задан, то можно использовать ряд тригонометрических идентичностей для вычисления косинуса. Например, косинус угла можно найти по синусу другого угла или по тангенсу угла. Для этого можно воспользоваться соотношениями: cos(α) = sin(90°-α) и cos(α) = 1 / tan(α).
Также можно использовать ряд «особых» углов, для которых косинусы известны и могут быть использованы для вычисления косинуса других углов. Например, косинусы углов 0°, 30°, 45°, 60° и 90° можно запомнить и использовать в дальнейших вычислениях. Например, если нам нужно найти косинус 45°, мы можем записать его как корень из двух деленный на два: cos(45°) = √2 / 2.
| Угол (α) | Косинус (cos(α)) |
|---|---|
| 0° | 1 |
| 30° | √3 / 2 |
| 45° | √2 / 2 |
| 60° | 1 / 2 |
| 90° | 0 |
Таким образом, вычисление косинуса угла без использования таблиц возможно при использовании простых математических свойств и идентичностей. Это позволяет находить значения косинуса угла в разнообразных ситуациях, не требуя доступа к внешнему источнику информации.
Использование калькулятора для определения значения косинуса угла
Важно отметить, что калькуляторы для расчета косинуса угла часто также предоставляют возможность вычисления синуса и тангенса угла, а также обратных функций, таких как арккосинус, арксинус и арктангенс. Таким образом, можно легко получить все необходимые значения тригонометрических функций для работы с углами в различных задачах.
Использование калькулятора для расчета косинуса угла удобно и эффективно, особенно при работе с углами, требующими точных значений. Благодаря этому инструменту можно сэкономить время и избежать ошибок при выполнении математических операций. В дополнение к этому, некоторые калькуляторы предлагают расширенные функции, такие как сохранение истории расчетов, работа с различными системами счисления и возможность установки угловой единицы измерения по умолчанию.
Практическое применение косинуса угла в различных областях

В астрономии, косинус угла находит применение при расчете расстояний до звезд, где используется метод параллакса. Он также используется для определения высоты небесных тел и их углового расстояния друг от друга.
В физике косинус угла применяется для расчета механических величин, таких как сила и мощность. Он позволяет определить проекцию вектора на оси координат и тем самым найти компоненту вектора вдоль определенного направления.
Косинус угла имеет применение в геометрии при изучении треугольников и других многоугольников. Он позволяет находить длину сторон и углы, а также определять, является ли треугольник прямоугольным, остроугольным или тупоугольным.
В инженерии, косинус угла используется при проектировании и строительстве. Например, при расчете нагрузок на конструкции, применении силы трения и определении углов наклона плоскостей. Он также необходим при решении задач механики, динамики и термодинамики.
Необходимо заметить, что косинус угла широко применяется не только в научных и технических областях, но также в повседневной жизни. Он встречается в навигации и картографии, где используется для определение координат и направлений движения. А также в компьютерной графике и играх для создания реалистичных эффектов и анимации объектов.
Таким образом, косинус угла играет важную роль в различных областях знаний и имеет множество практических применений. Знание этой функции позволяет решать сложные проблемы, основываясь на геометрических и тригонометрических связях между различными параметрами.
Важные свойства и особенности косинуса угла
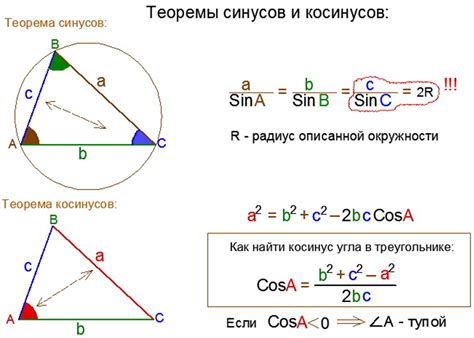
Связь с геометрией: Косинус угла может быть определен как отношение длины прилежащего катета прямоугольного треугольника к гипотенузе. Это геометрическое представление позволяет нам интерпретировать косинус угла в контексте физических и пространственных задач.
Периодичность и ограничения: Косинус угла имеет периодическую природу, что означает, что его значение повторяется через определенные промежутки. Отметим, что косинус угла ограничен от -1 до 1, что обусловлено его природой исходя из связи с относительными длинами сторон прямоугольного треугольника.
Свойство симметрии: Косинус угла обладает свойством симметрии относительно оси ординат. Это значит, что значение косинуса для углов x и -x будет одинаково. Такое свойство позволяет нам использовать симметричные значения для упрощения расчетов и анализа функции.
Связь с другими тригонометрическими функциями: Косинус угла имеет тесную связь с другими тригонометрическими функциями, такими как синус и тангенс. Например, синус угла может быть выражен через косинус как квадратный корень из разности единицы и квадрата косинуса. Это связь помогает нам переходить от вычисления одной тригонометрической функции к другой.
Применение в физике и математике: Косинус угла широко применяется в физике, механике, геометрии и других областях науки. Он используется для моделирования и анализа колебательных процессов, расчета векторных и силовых характеристик, а также для описания геометрических свойств объектов и пространственных конструкций.
Изучение свойств и особенностей косинуса угла позволяет нам более глубоко разобраться в его сути и применении. Понимание этих свойств поможет нам более эффективно использовать косинус угла в различных задачах и областях знаний.
Вопрос-ответ

Как найти косинус угла?
Для нахождения косинуса угла можно использовать несколько методов. Один из самых популярных способов - использование тригонометрической окружности. На ней можно построить треугольник, в котором между радиусом и хордой угол будет заданным. Зная значения радиуса и хорды, можно найти косинус угла с помощью формулы cos(угол) = значение хорды / значение радиуса. Еще один способ - использование тригонометрических таблиц или калькулятора, где значения косинуса углов уже предварительно посчитаны.
Как можно расчитать косинус угла без использования тригонометрической окружности?
Если нет возможности использовать тригонометрическую окружность, косинус угла можно рассчитать с помощью математического выражения. Для этого можно использовать формулу косинуса через расстояние между двумя точками на графике функции синуса. То есть, косинус угла можно рассчитать по формуле cos(угол) = координата x / длина отрезка, где координата x - значение на оси абсцисс, а длина отрезка - расстояние между этой точкой и началом координат.
Как использовать тригонометрические таблицы для расчета косинуса угла?
При использовании тригонометрических таблиц для расчета косинуса угла нужно найти значение угла в таблице и посмотреть его соответствующее значение косинуса. Так, если в таблице имеется значение угла 30 градусов, то значение косинуса этого угла будет равно 0,866. Если угол не находится в таблице, то можно использовать приближенное значение, ближайшее к нужному углу.
Как можно использовать калькулятор для расчета косинуса угла?
С помощью калькулятора можно рассчитать косинус угла, если в нем есть функция тригонометрического расчета. Нужно открыть калькулятор, найти функцию cos, ввести значение угла и нажать кнопку "=" или "Enter". Калькулятор автоматически рассчитает и выведет значение косинуса этого угла. Если на калькуляторе нет функции тригонометрического расчета, можно воспользоваться онлайн-калькулятором, где такая функция будет доступна.



