Существует удивительное разделение пространства, которое подарит вам новые знания и умения. Откройте для себя fascinans - таинственную область геометрии, которая открывает перед нами бесконечные возможности. Благодаря своей неординарности и изысканности, она берет нас за руку и ведет по пути открытий и откровений. Вместе мы откроем ушедший мир настоящих знаний, расширим словарный запас и научимся решать самые интересные задачи.
Поприветствуйте трапецию - чудо геометрической архитектуры! Она виртуозно сочетает в себе прямоту и изгибы, симметрию и асимметрию. Этот многоугольник сразу привлекает внимание своим нетривиальным обликом. Но не смотря на свою оригинальность, она надежно укрепляет свое место среди других фигур и оказывается полезной во многих практических применениях.
Каждая трапеция обладает своей площадью, своим собственным следом на пространственной картине. Величина этой площади является одним из ключевых параметров для понимания и изучения трапеции. Она позволяет нам оценить степень ее размерности и представить наполненное пространство, которое она занимает. Рассмотрим особенности и специфику методов нахождения площади трапеции на клетчатой сетке, чтобы разгадать ее геометрический код и поближе познакомиться с ее прелестями.
Что такое трапеция и как она представлена на клетчатой сетке?

Определение длин оснований трапеции на клетчатой сетке

Для определения длины оснований трапеции на клетчатой сетке можно использовать несложные алгоритмы или формулы, которые позволяют вычислить их значение.
- Метод 1: Визуальное определение длин оснований
- Метод 2: Использование горизонтальных отрезков
- Метод 3: Использование вертикальных отрезков
- Метод 4: Использование формулы площади трапеции
Один из способов определить длины оснований трапеции - визуально измерить их на клетчатой сетке. Для этого используются отметки и шкалы на клетках. Находясь на каждом основании трапеции, мы можем посчитать количество пересечений сетки и определить его значение.
Если трапеция расположена на клетчатой сетке горизонтально, мы можем использовать горизонтальные отрезки, простирающиеся от одного основания до другого. Определяя количество пересечений этих отрезков с клетками сетки, можем вычислить длину оснований.
Если трапеция расположена на клетчатой сетке вертикально, можем использовать вертикальные отрезки, простирающиеся от одного основания до другого. Счет количества пересечений этих отрезков с клетками позволяет нам определить длины оснований.
Также с помощью формулы для расчета площади трапеции можно выразить длины оснований через значение площади и высоты. Это можно сделать путем перестановки элементов в изначальной формуле и последующего вычисления.
Определение высоты трапеции на сетке

Раздел будет рассматривать способы определения высоты трапеции на клетчатой сетке, не прибегая к использованию конкретных терминов. Мы изучим методы для определения расстояния между сторонами трапеции с использованием синонимов для понятий "высота", "трапеция" и "сетка".
Расстояние между основаниями
Одним из способов определения высоты трапеции на клетчатой сетке является вычисление расстояния между ее сторонами, которые называются "основаниями". Мы можем использовать слова "расстояние между более длинной и менее длинной сторонами" для описания этого понятия. Для определения этого расстояния необходимо использовать синонимы для слов "основание" и "расстояние".
Построение перпендикуляра
Другой способ определения высоты трапеции заключается в построении перпендикуляра из вершины трапеции на основание. С помощью синонимов мы можем описать шаги построения перпендикуляра и его связь с определением высоты. Используя синонимы "построение прямой, перпендикулярной основанию" и "взаимное расположение вершины и основания", мы сможем более точно и понятно объяснить данный метод.
Определение площади трапеции на основе длин оснований и высоты

Сообщество математиков совершило важное открытие, которое позволяет вычислить площадь трапеции, используя значения длин оснований и высоты. Этот результат оказался особенно полезным в решении задач, связанных с геометрией и построениями.
Суть метода заключается в следующем: площадь трапеции можно выразить как половину произведения суммы длин оснований и высоты. Эта формула является доказанным утверждением и может быть использована для определения площади трапеции в различных задачах.
Применение геометрических принципов на клетчатой сетке для вычисления площади трапеции

При решении задачи на нахождение площади трапеции на клетчатой сетке мы можем разделить ее на более простые фигуры, такие как прямоугольники и треугольники. Затем мы можем вычислить площадь каждой фигуры и сложить их вместе, получая итоговую площадь трапеции.
Примеры решения задач могут включать разные размеры и формы трапеции, что позволяет учащимся видеть применение геометрических принципов на практике. Например, можно рассмотреть задачи, где трапеция имеет неравные основания или наклонные стороны.
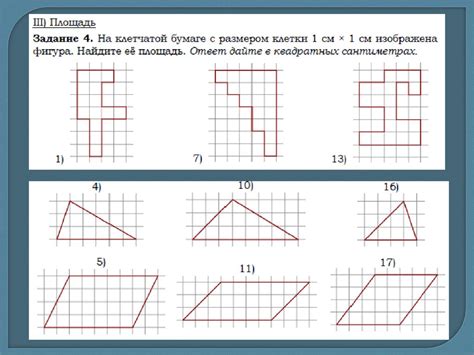
Для наглядности, можно использовать графическое представление клетчатой сетки с уже нарисованной трапецией, а также указать количество клеток, охватываемых каждой стороной. Такой подход помогает учащимся визуализировать действия и провести необходимые вычисления с учетом граничных условий.
Понимание и применение геометрических правил на клетчатой сетке может быть очень полезным для учащихся, так как оно развивает их способности анализировать и решать математические проблемы. Кроме того, оно помогает им понять, как геометрические принципы могут быть применены на практике в реальной жизни.
Практическое применение геометрии на клетчатой поверхности
Рассмотрим примеры конкретных ситуаций, когда знание площади трапеции возможно применить. Например, при проектировании крыши дома, зная площадь трапеции, можно точно рассчитать количество материала, необходимого для покрытия крыши. В архитектуре, зная площадь трапеции, можно определить стоимость отделки фасада здания. В географии, площадь трапеции может помочь определить площадь поля, района или города. Даже в медицине, площадь трапеции может быть использована при расчете площади поврежденной кожи или раны.
Поэтому, понимание и умение находить площадь трапеции на клетчатой сетке не только помогает в решении математических задач, но и имеет широкое практическое применение в реальной жизни. Знания геометрии и умение работать с трапециями позволяют решать проблемы из разных сфер, где требуется точное определение площади фигуры на клетчатой поверхности.
Вопрос-ответ

Как рассчитать площадь трапеции на клетчатой сетке?
Чтобы рассчитать площадь трапеции на клетчатой сетке, нужно разделить трапецию на две фигуры - прямоугольник и два треугольника. Затем нужно определить площадь каждой отдельной фигуры и сложить их. Для этого можно использовать формулу площади прямоугольника (произведение длины и ширины) и формулу площади треугольника (половина произведения основания и высоты). Полученные значения нужно сложить и тем самым получить площадь всей трапеции.
Как определить длину оснований трапеции на клетчатой сетке?
Чтобы определить длину оснований трапеции на клетчатой сетке, нужно посчитать количество клеток по каждому основанию. Количество клеток считается по количеству точек на основании, исключая конечные точки, которые не являются границами оснований. После подсчета количества клеток на каждом основании, полученные значения можно использовать для расчета площади трапеции.
Как определить высоту трапеции на клетчатой сетке?
Чтобы определить высоту трапеции на клетчатой сетке, нужно провести перпендикуляр к одному из оснований трапеции и определить количество клеток, которые пересекает этот перпендикуляр. Количество клеток будет соответствовать высоте трапеции. После определения высоты, ее можно использовать в формуле для расчета площади трапеции на клетчатой сетке.
Могу ли я использовать формулу для площади трапеции на клетчатой сетке, если стороны трапеции не параллельны клеткам сетки?
Если стороны трапеции не параллельны клеткам сетки, то использование обычной формулы для площади трапеции на клетчатой сетке может быть некорректным. В таком случае, необходимо рассмотреть каждую фигуру (прямоугольник и треугольники), на которые можно разделить трапецию, и использовать соответствующие формулы для их площадей. Затем полученные значения нужно сложить, чтобы получить общую площадь трапеции.
Как найти площадь трапеции на клетчатой сетке в 9 классе?
Для того чтобы найти площадь трапеции на клетчатой сетке в 9 классе, нужно знать формулу площади трапеции и уметь применять ее. Формула площади трапеции выглядит следующим образом: S = ((a + b) * h) / 2, где a и b - длины оснований трапеции, а h - высота трапеции. Для нахождения площади на клетчатой сетке, нужно просто подсчитать количество квадратных клеток, находящихся внутри трапеции, и отобразить их количество в ответе.



