В мире геометрии существует множество параметров и понятий, которые служат основой для решения разнообразных задач и проблем. Одним из важных элементов является угол, который определяет взаимное положение двух прямых линий или плоскостей. Угол имеет свои уникальные свойства, и одним из них является его тангенс.
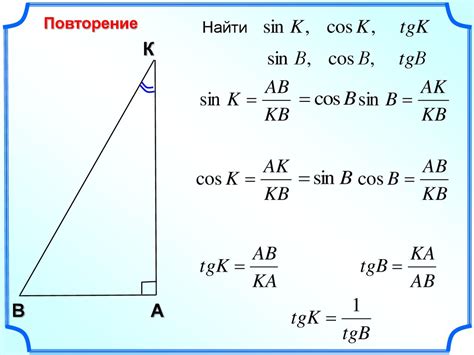
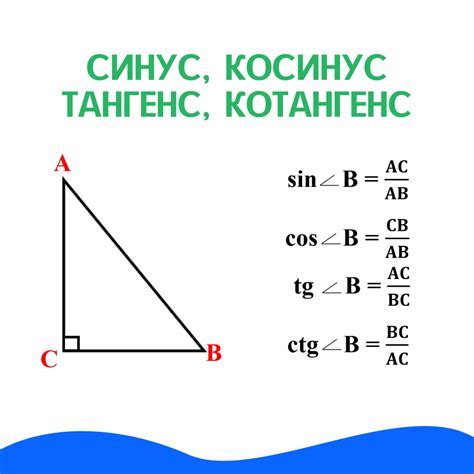
Тангенс – это тригонометрическая функция, определяющая отношение противоположной стороны прямоугольного треугольника к прилежащей стороне. Она является одним из основных инструментов для расчетов в геометрии и тригонометрии, обладая возможностью вычислять углы и их значения. Именно здесь тангенс приобретает свою значимость и становится неотъемлемой частью задач, связанных с нахождением углов в геометрии.
Один из интересных вопросов, возникающих в геометрии, заключается в определении значения угла при известном тангенсе. Зная значение тангенса, можно произвести обратные расчеты и получить необходимый угол. Это позволяет решать разнообразные задачи, связанные с построением и измерением углов в системе координат.
Тангенс и его значимость
В математике существует важный тригонометрический параметр, известный как тангенс. Он играет значительную роль при решении различных задач, связанных с геометрией и физикой. Тангенс позволяет определить соотношение между двумя сторонами прямоугольного треугольника и соответствующими углами.
Тангенс – это натуральная функция, определенная как отношение противолежащего катета к прилежащему катету прямоугольного треугольника. Он может быть выражен числовым значением или в виде отношения двух сторон.
Значение тангенса может быть положительным, отрицательным или нулевым, в зависимости от положения угла в круге единичного радиуса. Часто встречающееся значение тангенса – 0.75, означает, что противолежащий катет в прямоугольном треугольнике составляет 0.75 от длины прилежащего катета.
В следующих разделах статьи мы рассмотрим более подробно свойства и применение тангенса, а также способы его расчета и использования для нахождения значений углов в разнообразных ситуациях.
Тангенс: его сущность и практическое применение

Тангенс является одним из основных тригонометрических соотношений, которые помогают определить соотношения между углами и сторонами в треугольниках. Он выражает отношение противолежащего катета и прилежащего катета в прямоугольном треугольнике.
Зачем нам нужен тангенс? Представьте ситуацию, когда вы хотите рассчитать высоту здания, но нет возможности подняться на самую высокую точку и измерить угол наклона определенного отрезка. В этом случае можно использовать тангенс, чтобы определить угол, исходя из отношения высоты здания и расстояния до него. Также тангенс находит практическое применение в физике, инженерии, навигации, астрономии и других областях, где требуется анализ углов и отношений между величинами.
- Тангенс может быть использован для решения задач высотной геодезии, например, при определении высоты горы или здания.
- В физике тангенс позволяет определить силу трения или угол наклона плоскости.
- В навигации тангенс помогает определить направление движения судна или самолета.
- В астрономии тангенс используется для определения угловых размеров небесных тел.
Определение тангенса угла и его значения дает возможность более точного анализа и решения проблем, связанных с геометрией, физикой и другими науками. Знание и понимание тангенса позволяют решать сложные геометрические задачи и применять его в различных сферах деятельности.
Значение тангенса угла: подходы к вычислению и использование

Если вам необходимо определить тангенс угла, существуют различные методы вычисления этой величины. На практике есть несколько подходов, позволяющих найти значение тангенса угла, используя доступные данные и математические инструменты.
Один из популярных методов – использование специальных таблиц или калькуляторов, которые предоставляют готовые значения тангенса для различных углов. Это позволяет быстро и просто получить необходимые результаты.
Если у вас отсутствуют таблицы или калькуляторы, можно воспользоваться формулами, связывающими тангенс с другими тригонометрическими функциями. Например, определить тангенс угла можно с использованием синуса и косинуса, зная, что тангенс равен отношению синуса к косинусу угла.
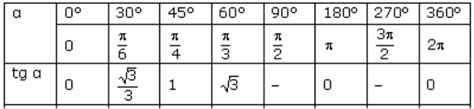
Кроме того, для некоторых особых углов существуют простые и запоминающиеся значения тангенса, например, для 0°, 30°, 45°, 60° и 90°. Зная эти значения, можно использовать алгоритмы и формулы для нахождения тангенса для других значений углов.
- Использование таблиц или калькуляторов для быстрого определения значения тангенса угла.
- Вычисление тангенса угла с использованием формул, связывающих его с синусом и косинусом.
- Запоминание простых значений тангенса для особых углов и использование их для вычисления тангенса других углов.
Значение тангенса 0.75: глубокий взгляд на углы и их соотношения
Тангенс - это математическая функция, описывающая соотношение между двумя сторонами прямоугольного треугольника. Значение тангенса угла можно выразить как отношение противоположного катета к прилежащему катету. То есть, если мы знаем значения сторон треугольника, мы можем вычислить тангенс угла.
- Значение тангенса 0.75 соответствует определенному углу, который мы можем найти, используя тригонометрические таблицы, калькуляторы или специальные программы.
- Это значение является числовым представлением соотношения сторон треугольника, где отношение противоположного катета к прилежащему составляет 0.75.
- Зная значение тангенса 0.75, мы можем провести обратный расчёт и найти угол, соответствующий данному значению.
- Значение тангенса 0.75 является одним из многих значений, которые могут быть использованы для анализа и моделирования различных физических и геометрических явлений.
- Изучая значения тангенса, мы можем лучше понять, как связаны углы и стороны треугольника, а также как эти соотношения могут применяться в практических задачах различных дисциплин.
Таким образом, значение тангенса 0.75 представляет интерес и имеет свои применения в науке и реальном мире, помогая нам лучше разобраться в углах и их соотношениях.
Методы определения угла по известному значению тангенса
В математике часто требуется определить угол по известному значению его тангенса. Существует несколько способов вычислить этот угол, которые базируются на различных математических свойствах и формулах.
| Метод | Описание |
|---|---|
| Использование таблицы значений тангенса | Один из простых способов определения угла по его тангенсу - использование таблицы значений тангенса. Таблица предоставляет соответствующие значения тангенса для различных углов. Находя ближайшее значение тангенса к заданному, можно определить приближенное значение угла. |
| Применение обратной функции тангенса | Обратная функция тангенса, обозначаемая как arctan или atan, позволяет вычислить угол по его тангенсу. Используя математические инструменты, можно вычислить угол при помощи обратной функции тангенса, зная его тангенс. |
| Использование треугольников с заданным тангенсом | Другим методом определения угла при заданном тангенсе является использование треугольников соответствующей пропорциональности. Построение треугольника с углом, значение тангенса которого известно, позволяет определить значение самого угла. |
Каждый из перечисленных методов имеет свои преимущества и ограничения, поэтому выбор конкретного метода зависит от конкретной задачи и имеющихся данных. С помощью этих способов можно точно или приближенно определить значение угла при заданном значении тангенса в различных контекстах и областях применения.
Использование таблиц и калькуляторов для определения угла при значении тангенса 0.75
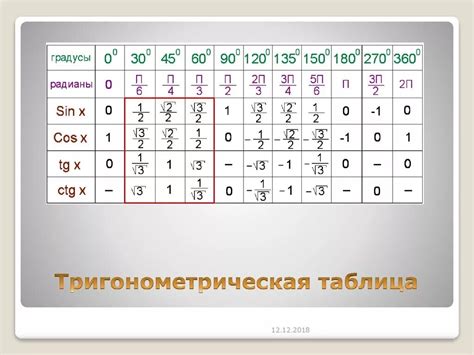
Одним из способов решения этой задачи является использование таблицы тангенсов. Таблица тангенсов представляет собой перечень углов и соответствующих им значений тангенса. Поскольку мы знаем, что тангенс представляет отношение противоположного катета к прилежащему катету в прямоугольном треугольнике, мы можем найти соответствующий угол в таблице, обращаясь к значениям тангенса.
Кроме того, можно воспользоваться онлайн-калькулятором тригонометрических функций для вычисления угла при заданном значении тангенса. Подавая в калькулятор значение тангенса 0.75, мы получим соответствующий угол в градусах. Такие калькуляторы удобны в использовании и могут быть полезны при решении различных задач, связанных с тригонометрией.
Методы вычисления угла при тангенсе 0.75 с применением тригонометрических формул

В данном разделе мы рассмотрим различные методы определения значения угла, если известен его тангенс и равен 0.75. Мы исследуем связь между тангенсом угла и его значением, применяя тригонометрические формулы.
Первый метод основывается на применении тригонометрической формулы, связывающей тангенс и синус угла. Из этой формулы можно выразить синус угла через тангенс, что позволит нам определить значение угла при заданном тангенсе 0.75.
Второй метод использует обратную тригонометрическую функцию арктангенс. С помощью этой функции мы сможем определить значение угла, при котором его тангенс равен 0.75. Арктангенс обратен к тангенсу и позволяет нам вычислить угол по его тангенсу, соблюдая соответствующий диапазон значений.
Третий метод основан на использовании тригонометрической формулы, связывающей тангенс с котангенсом угла. С помощью этой формулы можно выразить котангенс через тангенс и обратно, что даст возможность найти значение угла при тангенсе 0.75.
Все эти методы предоставляют различные подходы к нахождению угла, используя значение его тангенса. Выбор конкретного метода зависит от конкретных условий задачи и предпочтений пользователя. Определение угла при заданном тангенсе может быть полезным для решения геометрических и физических задач, где требуется знание угловых величин.
Примеры решения уравнений с тангенсом для определения значения угла при тангенсе 0.75

Мы рассмотрим несколько примеров, как можно решить уравнения с тангенсом, чтобы найти значение неизвестного угла, когда известен тангенс этого угла, равный 0.75. Все примеры будут подробно объяснены, чтобы помочь вам лучше понять процесс и применить его в дальнейших решениях.
Итак, начнем с первого примера:
Дано: тангенс угла = 0.75
Решение:
- Применим определение тангенса: тангенс угла равен отношению противолежащего катета к прилежащему катету треугольника.
- Обозначим противолежащий катет через a и прилежащий катет через b.
- Подставим известное значение тангенса и полученные обозначения в определение: 0.75 = a/b.
- Умножим обе части уравнения на b, чтобы избавиться от деления: 0.75b = a.
- Теперь мы можем использовать теорему Пифагора: a² + b² = c², где c - гипотенуза треугольника.
- Подставим найденное значение a в уравнение Пифагора: (0.75b)² + b² = c².
- Раскроем скобки и упростим уравнение: 0.5625b² + b² = c².
- Факторизуем уравнение, чтобы найти значение b: b²(0.5625 + 1) = c².
- Суммируем коэффициенты перед b²: 1.5625b² = c².
- Теперь возьмем квадратный корень от обеих частей уравнения, чтобы найти b: b = √(c²/1.5625).
- Наконец, мы можем найти угол, используя формулу: угол = arctg(a/b).
- Подставим найденные значения a и b: угол = arctg((0.75b)/b).
- Упростим уравнение и рассчитаем угол с помощью тригонометрической функции.
Таким образом, примеры решения уравнений с тангенсом дают нам возможность найти значения неизвестных углов при известных значений тангенса. Используя эти методы, мы можем более точно определить размеры и формы геометрических фигур или решить другие задачи, требующие знания углов и тригонометрических функций.
Вопрос-ответ

Как найти значение угла при тангенсе 0.75?
Чтобы найти значение угла, при котором тангенс равен 0.75, можно воспользоваться обратной функцией тангенса - арктангенсом. То есть нам нужно найти значение угла x, для которого tg(x) = 0.75. Для более точного результата, мы могли бы воспользоваться тригонометрической таблицей или калькулятором, но в данном случае мы предположим, что угол находится в диапазоне от -90 до 90 градусов. Таким образом, арктангенс от 0.75 равняется примерно 36.87 градусов.
Каким образом можно найти значение угла, когда известен тангенс 0.75?
Если вам известен тангенс угла, равный 0.75, вам потребуется воспользоваться обратной функцией тангенса, также известной как арктангенс. Вы можете использовать калькулятор или тригонометрическую таблицу, чтобы найти значение угла. В данном случае, результат будет приблизительно равен 36.87 градусов.
Как найти угол, когда значение тангенса составляет 0.75?
Для того чтобы найти значение угла, при котором тангенс равен 0.75, можно использовать обратную функцию тангенса, арктангенс. Если у вас есть калькулятор с функцией арктангенса, просто введите значение 0.75, чтобы получить результат. В данном случае, угол будет примерно равен 36.87 градусов.
Каким образом можно определить угол, есои известен тангенс и его значение равно 0.75?
Если вам предоставлено значение тангенса, равное 0.75, вы можете использовать обратную функцию тангенса, арктангенс, чтобы определить значение угла. Для этого у вас может быть необходим компьютер, калькулятор или тригонометрическая таблица. Ответом будет значение приблизительно равное 36.87 градусов.



