В геометрии существует множество методов и инструментов, которые помогают нам решать различные задачи и находить ответы на интересующие вопросы. Один из таких методов - использование тангенса для вычисления значения угла в треугольнике. Тангенс - это математическая функция, определяющая отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике.
Для вычисления значения угла в треугольнике с помощью тангенса необходимо знать длины двух сторон треугольника и значение тангенса данного угла. В этом случае мы можем использовать тригонометрическое соотношение, которое связывает эти значения и позволяет нам найти искомый угол.
Использование тангенса для вычисления значения угла в треугольнике является важным инструментом в геометрии и находит применение во многих сферах нашей жизни. Этот метод позволяет нам решать разнообразные задачи, связанные с измерением углов, построением и нахождением неизвестных сторон треугольников. Неоценимая информация о тангенсе угла позволяет нам более точно анализировать и понимать геометрические объекты и явления.
Тангенс угла АОВ: основные понятия и определения

Отношение, которое мы ищем, зависит от линейных размеров треугольника, а именно его сторон и углов. Тангенс угла АОВ позволяет определить, насколько круто или полого выпуклый угол АОВ в треугольнике.
Тангенс угла АОВ можно выразить с помощью формулы: тангенс угла АОВ = противоположная сторона треугольника АОВ / прилежащая сторона треугольника АОВ. Зная значения этих сторон, мы можем вычислить тангенс угла АОВ и использовать его для решения различных геометрических задач.
Важно помнить, что тангенс угла АОВ может быть как положительным, так и отрицательным, в зависимости от положения угла АОВ относительно оси координат или иной опорной прямой. Отрицательный тангенс обозначает, что угол АОВ находится в определенной четверти плоскости.
Тангенс угла АОВ является важным понятием в геометрии и находит применение в различных областях, включая физику, инженерию и компьютерную графику. Понимание основных понятий и определений, связанных с тангенсом угла АОВ, позволяет решать сложные задачи и строить точные геометрические модели.
Знакомство с тангенсом и его геометрическим представлением
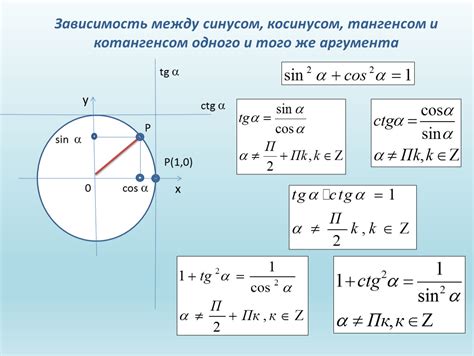
Тангенс является отношением стороны треугольника к соответствующему углу. Он позволяет определить, насколько крутой угол и какая сторона противоположна ему. Другими словами, тангенс показывает, насколько быстро изменяется высота относительно ширины.
Представим себе треугольник, где одна сторона вертикальна, а другая горизонтальна. Если мы проведем прямую линию от вершины треугольника до точки пересечения горизонтальной и вертикальной сторон, то получим еще одну, наклонную сторону. Тангенсом этого угла называется отношение высоты к ширине треугольника. Чем больше тангенс, тем круче угол между вертикальной и наклонной сторонами.
Итак, знание тангенса и его геометрического представления позволяет более глубоко понять геометрию и тригонометрию треугольников, а также применять его для решения различных задач и нахождения соотношений между сторонами и углами.
Определение тангенса угла между двумя сторонами треугольника и его вычисление
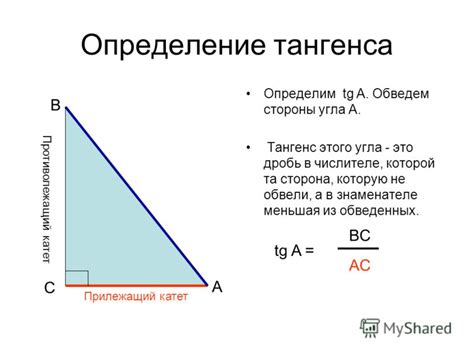
Тангенс угла обозначается как tg(α) и определяется как отношение противолежащей стороны к прилежащей стороне угла. Другими словами, тангенс угла равен отношению длины стороны, противолежащей углу, к длине смежной стороны угла.
Для вычисления тангенса угла необходимо знать значения длин сторон, противолежащей и смежной углу. После того, как эти значения известны, применяется формула вычисления тангенса, которая состоит из деления длины противолежащей стороны на длину смежной стороны:
tg(α) = a / b
Где a - длина противолежащей стороны, b - длина смежной стороны.
Вычисление тангенса угла позволяет получить числовое значение, которое может быть использовано для анализа треугольника и его углов. Знание тангенса угла позволяет более точно оценить геометрические свойства треугольника и его углов, а также применять его в различных задачах, связанных с тригонометрией и геометрией.
Вопрос-ответ

Как найти тангенс угла АОВ в треугольнике?
Для нахождения тангенса угла АОВ в треугольнике необходимо вычислить отношение противолежащей стороны к прилежащей стороне. Формула для вычисления тангенса угла равна тангенсу равнобедренного треугольника. В этой формуле, противолежащая сторона относится к прилежащей и обозначается как A, а угол обозначается как О. Таким образом, тангенс угла АОВ можно найти по формуле: tan(АОВ) = A/O.
Каким образом можно определить значения сторон A и O для нахождения тангенса угла АОВ?
Значения сторон A и O можно определить с помощью синуса и косинуса углов треугольника. Например, можно использовать формулу синусов, согласно которой сторона A равна произведению стороны О на синус угла А и косинус угла О. Эту формулу можно применить, когда известны значения угла А и стороны О. После нахождения значений сторон A и O, можно использовать ранее указанную формулу для нахождения тангенса угла АОВ.
Какой геометрический смысл имеет тангенс угла АОВ?
Тангенс угла АОВ в треугольнике имеет геометрический смысл в отношении противолежащей стороны к прилежащей стороне. Более конкретно, тангенс угла АОВ показывает, насколько быстро высота изменяется по сравнению со степенью изменения длины основания треугольника.
Существуют ли другие способы нахождения тангенса угла АОВ в треугольнике, кроме формулы для равнобедренного треугольника?
Да, существуют и другие способы нахождения тангенса угла АОВ в треугольнике. Например, можно использовать тригонометрический калькулятор или таблицу значений тангенсов углов. Также, если известны значения синуса и косинуса угла АОВ, можно применить формулу для нахождения тангенса, которая гласит: tan(АОВ) = sin(АОВ)/cos(АОВ).
Как найти тангенс угла АОВ в треугольнике?
Для нахождения тангенса угла АОВ в треугольнике можно воспользоваться формулой тангенса: tg(АОВ) = противоположная сторона/прилежащая сторона. Противоположная сторона - это сторона, напротив угла АОВ, прилежащая сторона - это сторона, образующая угол АОВ. Необходимо вычислить длины этих сторон, а затем разделить противоположную на прилежащую.



