Отправляясь в путешествие по миру геометрии, мы наверняка сталкиваемся с различными фигурами, способными оказать на нас глубокое впечатление. Одной из наиболее удивительных и элегантных форм является шар. Его совершенная симметрия и плавные изгибы вызывают ощущение гармонии и непревзойденной красоты. Но как же вычислить площадь такого сложного объекта без множества специальных инструментов и формул? Давайте откроем новый подход к изучению этого вопроса, проникая в таинственные глубины геометрии.
В наших поисках мы обратимся к основам математического анализа и геометрии, применяя необычные и, порой, захватывающие методики расчета. Нас ожидает настоящее путешествие во времени, где мы исследуем различные подходы в разные эпохи - от античности до современности. Вооружившись наукой и узнав о секретных формулах, мы сможем познакомиться с уникальными способами рассчитать площадь поверхности шара.
Готовы к удивительному открытию? Наше путешествие начинается прямо сейчас! Давайте отправимся вместе в мир геометрии, где найдем ответы на наши вопросы и откроем для себя новые горизонты знаний. Приготовьтесь окунуться в увлекательную головоломку, где каждое открытие искусно переплетается с практическими примерами, чтобы вы смогли на практике ощутить всю мощь и красоту геометрии!
Определение поверхности сферы
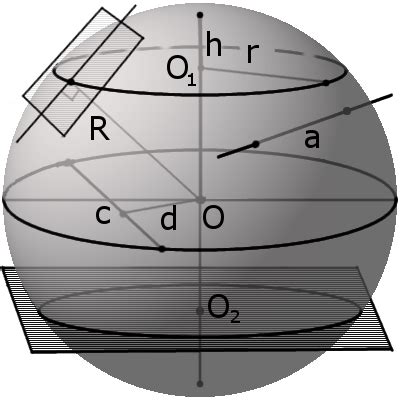
Метод интегрирования:
Один из методов определения площади поверхности сферы - использование математического интеграла. Сфера представляет собой поверхность, образованную вращением полуокружности вокруг ее диаметра. Для вычисления такой поверхности можно использовать формулу интеграла, представляющую собой сумму площадей бесконечно малых элементов поверхности.
Геометрический способ:
Другой способ определения площади поверхности шара - геометрический. В данном случае мы вычисляем площадь сферического сегмента - части поверхности сферы, ограниченной двумя плоскостями и дугой окружности. Затем, складывая площади всех сегментов, получаем общую площадь поверхности сферы.
Формула:
Также существует математическая формула для расчета площади поверхности шара. Площадь поверхности сферы равна произведению ее радиуса на удвоенное число π (пи).
Формула для вычисления площади сферы
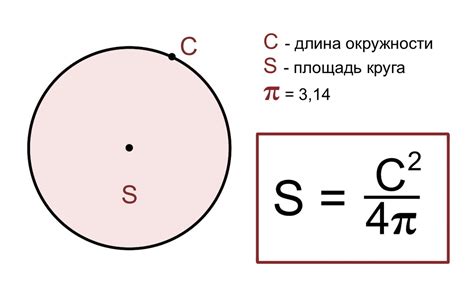
| Символ | Описание |
|---|---|
| π (пи) | Математическая константа, приближенное значение которой равно 3.14159 |
| r (радиус) | Расстояние от центра шара до любой его точки |
| S (площадь поверхности) | Площадь поверхности шара |
Для расчета площади поверхности шара необходимо умножить квадрат радиуса на 4, затем умножить полученный результат на значение математической константы π (пи). Таким образом, формула для вычисления площади поверхности шара имеет вид:
S = 4πr²
Где S - площадь поверхности шара, а r - радиус.
Зная радиус шара, можно легко применить данную формулу для определения площади поверхности и использовать результат в различных геометрических или физических задачах.
Шаги для применения формулы площади сферы
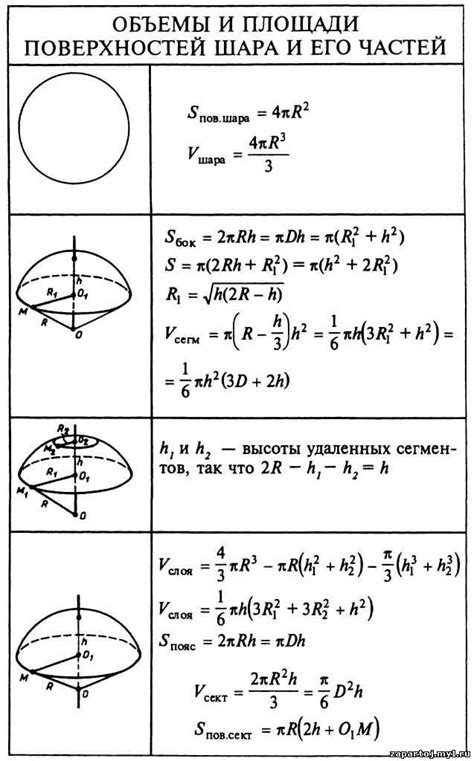
В этом разделе мы познакомимся с последовательностью шагов, которые позволят нам использовать формулу для расчета площади сферы. Мы узнаем, как применить эту формулу к конкретным данным, чтобы получить точный результат. Благодаря этим шагам, мы сможем на практике применить знания о площадях шаров и использовать их в различных ситуациях.
Пример 1: Расчет площади шара с известным радиусом
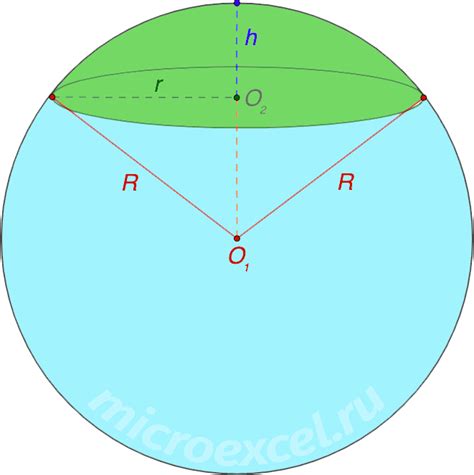
В данном примере рассмотрим способы вычисления поверхности шара, основываясь на знании его радиуса. Расчет площади шара позволяет определить, сколько поверхности должно быть покрыто однородным материалом для полного его закрытия.
Для начала, нам необходимо запомнить, что радиус - это расстояние от центра шара до любой его точки. В данном примере, мы считаем, что радиус уже известен.
Площадь поверхности шара рассчитывается по формуле:
S = 4πr²
Здесь символ "π" представляет собой математическую константу, приближенное значение которой равно 3,14159. Символ "r" обозначает радиус шара.
Давайте рассмотрим пример: если радиус шара составляет 5 единиц, то площадь поверхности будет:
S = 4π(5)² = 4π(25) = 100π
Таким образом, площадь поверхности шара с радиусом 5 единиц равна 100π.
Пример 2: Вычисление поверхности шара по известной диаметральной проекции

В этом примере мы рассмотрим метод расчета площади поверхности шара, исходя из известной диаметральной проекции. Диаметральная проекция представляет собой отображение шара на плоскость, с указанием диаметра. Используя эту информацию, мы сможем определить площадь поверхности шара без прямого измерения радиуса.
Для начала, нам необходимо найти радиус шара, исходя из известной диаметральной проекции. Диаметр - это двойное значение радиуса, поэтому нам нужно разделить его на два, чтобы получить радиус. После этого, мы сможем использовать формулу для расчета площади поверхности шара.
| Шаг | Формула | Пример |
|---|---|---|
| 1 | Рассчитываем радиус | Если известна диаметральная проекция D, то радиус r = D/2 |
| 2 | Вычисляем площадь поверхности шара | S = 4πr² |
Таким образом, площадь поверхности шара может быть рассчитана, используя известную диаметральную проекцию. Следуя указанным шагам, мы можем определить площадь поверхности шара, даже если точные измерения радиуса недоступны.
Пример 3: Расчет площади шара с использованием объема
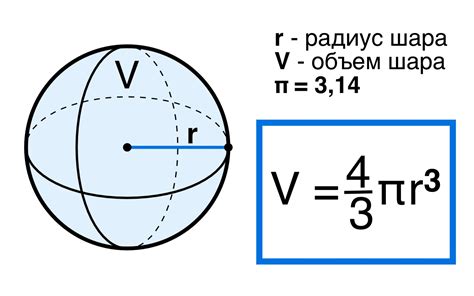
Используя формулу для расчета объема шара, которая выражается через радиус (V = 4/3 * π * r^3), мы можем перейти к формуле для вычисления площади шара. Рассмотрим следующую формулу:
S = 4 * π * r^2
Здесь S обозначает площадь шара, а r - радиус. Используя значение радиуса и формулу для площади, мы можем получить точную площадь поверхности шара.
Советы и рекомендации для упрощения вычислений

В этом разделе мы поделимся с вами некоторыми полезными советами и рекомендациями, которые помогут упростить процесс вычислений. Знание этих методов поможет вам не только в расчете площади шара и других геометрических фигур, но и в разных областях повседневной жизни.
- Используйте формулы и теоремы в своих вычислениях для определения правильного подхода и последовательности действий.
- Разбейте сложные задачи на более простые подзадачи, чтобы сделать их более управляемыми и понятными.
- Воспользуйтесь графическими инструментами или схемами для визуализации проблемы и упрощения ее анализа.
- Если возможно, используйте алгоритмы, программы или онлайн-калькуляторы для автоматизации вычислений и сокращения времени, затрачиваемого на ручные расчеты.
- Не бойтесь пробовать разные подходы или методы для решения задачи. Иногда находясь в поиске оптимального решения, вы можете обнаружить новые и более простые способы решения проблемы.
- Не забывайте о проверке своих ответов и результатов, чтобы избежать ошибок и уточнить точность вычислений.
Эти советы и рекомендации могут быть полезными не только при расчете площади шара, но и во многих других математических и научных задачах. Используйте их, чтобы сделать вашу жизнь проще и вашу работу более эффективной.
Особенности расчета площади шара в различных системах измерения
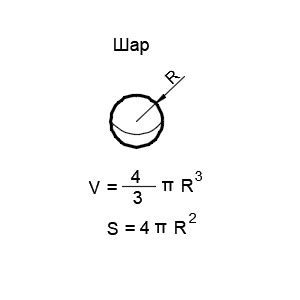
В данном разделе рассмотрим основные аспекты расчета площади поверхности шара в разных системах измерения. Обратим внимание на специфические особенности, связанные с применением различных единиц измерения и формул расчета.
Переходя к расчету площади шара в международной системе единиц (СИ), используется формула, основанная на радиусе шара. Эта формула выражается через константу Пи (π) и задействует квадратный корень. В СИ площадь шара вычисляется по формуле: S = 4πr^2, где S - площадь поверхности шара, r - радиус шара.
В отличие от СИ, в некоторых системах измерения, например, в американской системе, площадь шара может рассчитываться на основе диаметра, а не радиуса. Формула в этом случае будет зависеть от конкретных принятых в системе единиц измерения. Важно отметить, что при переводе диаметра в радиус необходимо провести соответствующие преобразования, чтобы использовать формулу СИ.
Кроме того, в разных системах измерения могут применяться различные единицы измерения площади, например, квадратные метры в СИ, дюймы квадратные в американской системе или аршины квадратные в русской системе. При расчете следует быть внимательным и использовать соответствующие формулы и конверсии между разными единицами измерения площади.
| Система измерения | Формула расчета площади шара |
|---|---|
| Международная система единиц (СИ) | S = 4πr^2 |
| Американская система единиц | Формула зависит от конкретных единиц измерения |
| Русская система единиц | Формула зависит от конкретных единиц измерения |
Применение площади шара в реальной жизни

Проектирование зданий и сооружений: Знание площади шара позволяет архитекторам и инженерам правильно распределять пространство и оптимизировать конструкцию для достижения наилучших результатов. Например, при проектировании куполов или крытых конструкций необходимо учесть площадь поверхности, чтобы обеспечить стабильность и эстетическую привлекательность.
Сфера физики и астрономии: Площадь шара играет важную роль в понимании законов гравитации и распределении энергии в системе. Поверхность шаровых объектов, таких как планеты, спутники и метеориты, влияет на их взаимодействие с окружающим пространством и другими телами.
Медицина и биология: В медицине и биологии площадь шара может быть полезной для определения объема и площади поверхности клеток, органов и тканей. Это помогает в оценке их функциональных свойств и разработке лекарственных препаратов, а также в определении плотности и концентрации веществ в организме.
География и картография: Площадь шара применяется при изучении и представлении географических и геологических данных на планете. Например, для определения площадей континентов, океанов, исследования форм территории или расчета объемов ресурсов на земле.
Разработка компьютерных игр и 3D графики: Площадь шара играет важную роль при создании виртуальных миров и объектов в компьютерных играх и 3D графике. Расчет площади поверхности объектов помогает создать реалистичные и интерактивные сцены, которые привлекают внимание и создают удовлетворяющий пользовательский опыт.
Во всех этих случаях, понимание и использование площади шара способствует более глубокому и полному анализу, позволяет сделать более обоснованные решения и достичь лучших результатов в различных областях деятельности.
Вопрос-ответ

Как рассчитать площадь шара?
Формула для расчета площади шара: S = 4 * π * r², где S - площадь шара, π - математическая константа, примерно равная 3,14159, а r - радиус шара.
Можете привести пример расчета площади шара?
Конечно! Предположим, у нас есть шар с радиусом 5 сантиметров. Для расчета его площади, мы используем формулу S = 4 * π * r²: S = 4 * 3,14159 * 5² = 4 * 3,14159 * 25 = 314,159 сантиметров в квадрате.
Какую единицу измерения используете для площади шара?
Площадь шара обычно измеряется в квадратных единицах длины, например, квадратные сантиметры, квадратные метры или квадратные дюймы.
Могу ли я использовать другую математическую константу вместо π для расчета площади шара?
Нет, для расчета площади шара необходимо использовать приближенное значение π, примерно равное 3,14159. Это связано с геометрией и свойствами окружности, из которых состоит шар.
Что мне делать, если у меня есть диаметр шара, а не радиус?
Если у вас есть диаметр шара, а не радиус, вы можете легко вычислить радиус, разделив значение диаметра на 2. Затем используйте полученный радиус для расчета площади шара по формуле S = 4 * π * r².



