Будучи одной из самых фундаментальных геометрических фигур, круг обладает множеством интересных свойств и характеристик. Одной из таких характеристик является его радиус, который определяет расстояние от центра круга до любой его точки. Но что делать, если известна только площадь круга, но неизвестен его радиус? Именно с этим вопросом мы и разберемся в данной статье.
Изучение методов и формул для нахождения радиуса круга по известной площади позволяет нам не только решить задачи геометрии, но и применить полученные знания в реальной жизни. Например, понимание этого процесса может быть полезным при проектировании круглых бассейнов, создании колес для автомобилей или даже при решении задач в программировании.
В дальнейшем мы рассмотрим несколько примеров и подробно обсудим различные способы решения задачи определения радиуса круга по известной площади. Каждый из представленных методов имеет свои особенности, преимущества и ограничения, поэтому выбор подходящего способа будет зависеть от конкретной ситуации и предпочтений исследователя.
Измерение неизвестного параметра окружности на основе площади: уникальные случаи и полезные подсказки

Когда имеется некоторое количество плоских фигур, количество и форма которых открывают огромные возможности для изучения и применения различных математических концепций, иногда возникает необходимость определить радиус круга, зная его площадь. В данном разделе мы рассмотрим редкие и интересные примеры таких случаев и поделимся полезными советами, чтобы помочь вам решить подобные задачи.
Расчёт радиуса круга по формуле площади
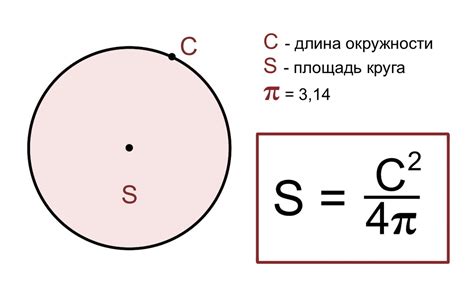
Метод 1: Использование формулы площади круга
Один из способов определить радиус круга, зная его площадь, - использование формулы площади круга. Формула состоит из математического выражения, соответствующего зависимости между площадью и радиусом. С помощью этой формулы можно легко вычислить радиус, если известна площадь.
Пример:
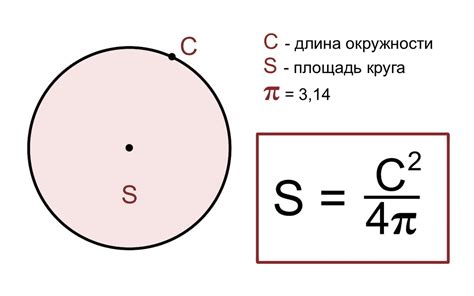
Допустим, у нас есть круг с площадью 25 квадратных единиц. Мы хотим определить его радиус. Воспользуемся формулой площади круга:
Площадь круга = π * радиус²
25 = π * радиус²
Для того чтобы найти радиус, нужно решить уравнение. Раскрыв скобку, получим:
25 = π * радиус * радиус
Затем делим обе стороны уравнения на π:
25 / π = радиус * радиус
Далее извлекаем квадратный корень обеих частей:
√(25 / π) = радиус
Результат: радиус ≈ 2,82
Таким образом, радиус круга с площадью 25 квадратных единиц составляет приблизительно 2,82 единицы.
Использование уравнения длины окружности для определения размера радиуса
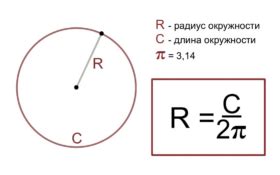
В данном разделе мы рассмотрим метод использования уравнения длины окружности для определения значения радиуса. Этот подход основан на связи между длиной окружности и радиусом, позволяя нам вычислить радиус на основе известной длины окружности.
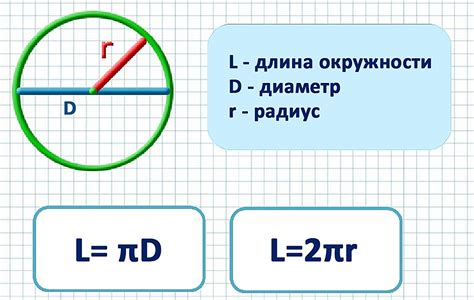
Уравнение длины окружности
Для начала, вспомним, что длина окружности можно вычислить по формуле: Длина_окружности=2π·Радиус. В данном уравнении символ π обозначает математическую константу, приближенное значение которой равно 3,14.
Таким образом, если нам известна длина окружности, мы можем использовать данное уравнение для вычисления значения радиуса. Для этого мы делим длину окружности на 2π, и полученный результат будет равен радиусу круга.
Практическое применение
Вычисление радиуса по известной длине окружности может быть полезным при работе с различными геометрическими задачами. Например, если вам нужно построить круг определенного размера или найти положение центра окружности относительно других объектов.
Использование уравнения длины окружности для нахождения радиуса позволяет нам точно определить размеры круга на основе известных данных. Этот подход особенно полезен в задачах, где требуется вычислить размеры круга без непосредственного измерения его радиуса.
Простой пример: нахождение размера круга с заданной площадью
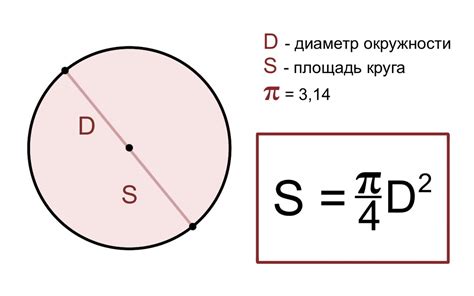
В данном разделе будет представлен пример простого способа определения размера круга, где известна только его площадь. Мы рассмотрим шаги, которые помогут вам находить радиус круга, используя доступные данные. Этот метод основан на математических принципах и может быть полезен в различных ситуациях, где требуется определить радиус круга с известной площадью.
Сложный пример: вычисление радиуса круга через площадь с помощью системы уравнений
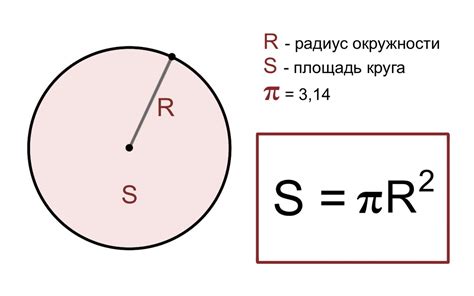
В этом разделе рассмотрим более сложный пример, в котором мы будем находить радиус круга через известную площадь, используя систему уравнений.
Для начала, обозначим неизвестный радиус круга как R. Зная площадь круга (S), мы можем поставить систему уравнений для вычисления R.
- Используя формулу для площади круга: S = π*R^2, мы можем записать уравнение: π*R^2 = S.
- Далее, мы можем привести это уравнение к виду, где R будет учитываться в единственном числе: R^2 = S/π.
- И, наконец, достаточно извлечь квадратный корень из обеих сторон уравнения, чтобы получить истинное значение радиуса: R = √(S/π).
Таким образом, применяя систему уравнений, мы можем вычислить радиус круга, если известна его площадь. Важно помнить, что значением π приближенно равно 3.14, однако для более точных расчетов можно использовать более точное значение π.
Использование онлайн-калькуляторов в поиске радиуса окружности

Когда требуется определить радиус окружности по известной площади, можно воспользоваться онлайн-калькуляторами, которые упрощают процесс и делают его более быстрым и удобным. Эти инструменты позволяют найти радиус, необходимый для построения круга, исходя из указанной площади.
Онлайн-калькуляторы для определения радиуса окружности обычно работают путем ввода известной площади в определенное поле и последующего нажатия кнопки "Рассчитать". Алгоритм, лежащий в их основе, обычно выполняет математическую формулу, чтобы найти соответствующий радиус круга.
Такие калькуляторы предоставляют возможность не только мгновенно получить результат, но и провести другие вычисления, такие как поиск диаметра или длины окружности по известному радиусу. Они могут быть полезными инструментами для всех, кто имеет дело с геометрическими вычислениями.
Использование онлайн-калькуляторов значительно упрощает нахождение радиуса круга по известной площади. Однако, всегда полезно знать основы математических формул для этого вычисления, чтобы проверить правильность результатов, полученных с помощью калькулятора.
Применение формулы площади для нахождения радиуса круга в реальных задачах
Решение геометрических задач
В математическом моделировании и архитектурном проектировании, необходимость в точных вычислениях и размерах кругов возникает во многих задачах. Например, при планировании участка, можно использовать формулу площади круга для определения размеров газона или садового пруда в зависимости от заданной площади. Также, в геодезии и картографии, можно использовать данную формулу для нахождения радиуса окружности, которая представляет собой границу определенной территории или земельного участка.
Вычисление объема контейнера
В различных промышленных отраслях, таких как производство пищевых продуктов или химическая промышленность, формула площади круга также может использоваться для определения радиуса контейнера или емкости, в которых хранятся различные вещества. Например, при проектировании емкости для газообразных продуктов или емкости для хранения продуктов питания, можно рассчитать необходимые размеры и объем контейнера, используя значения площади круга и других известных параметров.
Определение размеров колеса
В автомобильной и велосипедной индустрии, формула площади круга можно применить для определения радиуса колеса. Учитывая, что диаметр колеса имеет прямую зависимость от радиуса, зная площадь круга, можно рассчитать соответствующее значение радиуса. Это может быть полезно, например, при выборе правильного размера колеса для автомобиля или велосипеда при замене шин.
Таким образом, формула площади круга является универсальным инструментом для решения различных задач в реальных ситуациях. Зная значение площади и другие известные параметры, можно определить радиус круга и использовать это знание для принятия обоснованных решений в различных областях деятельности.
Секреты эффективного поиска радиуса окружности при известной площади
Когда речь заходит о вычислении радиуса окружности по известной площади, существуют несколько полезных советов, которые помогут вам достичь точного результата. Откройте для себя некоторые секреты эффективного и улучшенного подхода к данной задаче.
Отбросьте предубеждения
Первым шагом к успешному определению радиуса окружности является осознание важности отбрасывания предубеждений. Забудьте о стереотипах и подходах, которые ограничивают ваше мышление. Уравняйте свой ум и откройтесь для новых идей и методов.
Обратите внимание на формулы
Для вычисления радиуса окружности предлагается воспользоваться соответствующей математической формулой. Ознакомьтесь с разными формулами, которые связаны с радиусом окружности, и выберите ту, которая наиболее подходит для вашего конкретного случая. Обратите внимание на информацию о площади, которая может быть полезной при использовании формулы.
Используйте правильные единицы измерения
При решении задачи о нахождении радиуса окружности необходимо быть внимательным к выбору правильных единиц измерения для площади. Убедитесь в том, что вы используете одинаковые единицы измерения и правильные префиксы для упрощения расчетов. Это поможет избежать ошибок при получении ответа.
Разберитесь с алгебраическими операциями
Для эффективного поиска радиуса окружности по известной площади необходимо разобраться с алгебраическими операциями. Изучите основные понятия алгебры, такие как умножение, деление, сложение и вычитание. Постепенно крепкие знания в алгебре помогут вам легче понять и применять соответствующие формулы для нахождения радиуса окружности.
Экспериментируйте и проверяйте
Никогда не бойтесь экспериментировать и проверять свои результаты. При численных вычислениях проверяйте каждый шаг, чтобы исключить вероятность ошибок. Сравните ваш ответ с известными результатами или с другими способами определения радиуса окружности. Используйте различные значения площади и варьируйте их, чтобы понять, как они влияют на радиус.
Эти полезные советы помогут вам провести эффективный поиск радиуса окружности при известной площади. Важно помнить о правильном использовании формул, выборе правильных единиц измерения и тщательной проверке результатов. Применяйте эти советы и познакомьтесь с разными способами решения задачи, чтобы стать опытным в поиске радиуса круга.
Практические примеры и задачи для тренировки нахождения расстояния от центра до точки окружности по параметров фигуры

В этом разделе мы предлагаем ряд практических примеров и задач, которые помогут вам тренировать навык нахождения расстояния от центра до точки окружности по известным параметрам фигуры. При решении этих задач вам потребуется применить знания о площади и геометрических свойствах окружности.
Пример 1: Нахождение радиуса по площади круга
- Задача: Известна площадь круга, равная S = 64π квадратных единиц. Найдите радиус этого круга.
- Решение: Для начала воспользуемся формулой для площади круга: S = π * r^2, где S - площадь, r - радиус круга.
- Теперь, зная площадь круга, мы можем переписать формулу и выразить радиус: r^2 = S / π, r = √(S / π).
- Подставим значение площади из условия: r = √(64π / π), r = √64 = 8.
- Ответ: Радиус круга равен 8 единиц.
Пример 2: Задача на нахождение площади круга по радиусу
- Задача: Радиус круга равен 5 см. Найдите площадь этого круга.
- Решение: Для нахождения площади круга воспользуемся формулой S = π * r^2, где S - площадь, r - радиус круга.
- Подставим значение радиуса из условия: S = π * 5^2, S = 25π.
- Ответ: Площадь круга равна 25π квадратных сантиметров.
Пример 3: Нахождение радиуса по длине окружности
- Задача: Длина окружности равна 30π см. Найдите радиус этой окружности.
- Решение: Для нахождения радиуса окружности по длине воспользуемся формулой L = 2πr, где L - длина окружности, r - радиус.
- Перепишем формулу и выразим радиус: r = L / (2π).
- Подставим значение длины из условия: r = (30π) / (2π) = 15.
- Ответ: Радиус окружности равен 15 сантиметров.
Вопрос-ответ

Как найти радиус круга, если известна его площадь?
Для нахождения радиуса круга по известной площади необходимо использовать формулу: радиус = √(площадь / π), где π - математическая константа, примерно равная 3.14159. Данную формулу можно использовать для вычисления радиуса круга при любой площади.
Как применить формулу нахождения радиуса круга по известной площади?
Чтобы применить формулу нахождения радиуса круга по известной площади, нужно знать значение площади и подставить его в формулу радиуса (радиус = √(площадь / π)). После подстановки значения площади в формулу, следует произвести вычисления и полученный результат будет радиусом круга.
Какие примеры можно привести для нахождения радиуса круга по известной площади?
Например, если площадь круга равна 25 квадратным сантиметрам, чтобы найти радиус, нужно применить формулу: радиус = √(25 / π). Подставив значение площади и выполнив вычисления, получим результат вида радиус = √(25 / 3.14159), который можно примерно приблизить до радиус = √7.9577, а это примерно равно 2.82 сантиметра.
Какой совет можно дать при нахождении радиуса круга по известной площади?
При нахождении радиуса круга по известной площади рекомендуется использовать формулу и не забывать о значении математической константы π. Также стоит обратить внимание на единицы измерения площади и радиуса - они должны быть одинаковые. Если значение площади указано в квадратных сантиметрах, то и радиус нужно выразить в сантиметрах.



