Математика может быть интригующей и полезной наукою, способной разгадать самые запутанные головоломки и проблемы. Один из таких загадочных вопросов - определить высоту трапеции, зная лишь ее основания. Казалось бы, как можно вывести ответ без различных сложных формул и процедур? Но важно помнить, что даже в математике есть нестандартные подходы и простые методы, которые могут помочь решить эту задачу.
Обратимся к простым средствам математики: пусть у вас есть трапеция с известной длиной каждого ее основания. Как можно определить ее высоту без лишних трудностей? В нашем случае нам помогут базовые геометрические свойства и понимание сути фигуры.
Суть трапеции заключается в том, что она имеет две параллельные основания и четыре боковых стороны. При этом ее высота представляет собой перпендикулярную прямую, опущенную из одного основания на другое. Таким образом, высота трапеции является ключевым элементом, который позволяет измерить ее площадь и решить множество задач.
Способы вычисления высоты геометрической фигуры при известных значениях оснований

- Метод подобия треугольников
- Применение теоремы Пифагора
- Использование теоремы о пропорциональности площадей
Один из подходов к определению высоты трапеции заключается в использовании свойств подобных треугольников. В данном случае основания трапеции можно рассматривать как основания двух подобных треугольников, а высоту - как отрезок, соединяющий соответствующие вершины треугольников. Путем установления соответствующих пропорций и расчета известных значений, можно определить высоту трапеции.
В некоторых случаях, когда известны длины оснований и диагонали трапеции, можно использовать теорему Пифагора для вычисления высоты. При этом диагонали и высота трапеции образуют прямоугольный треугольник, в котором применяется знаменитая формула a^2 + b^2 = c^2, где a и b - длины одной диагонали и основания, а c - высота.
Еще один метод нахождения высоты трапеции заключается в применении теоремы о пропорциональности площадей. Согласно этой теореме, отношение площадей двух подобных фигур равно квадрату отношения длин соответствующих сторон. Применяя данную теорему к трапеции, можно выразить высоту через площади и длины оснований.
Зная основания трапеции, можно использовать различные методы и формулы для нахождения ее высоты. В зависимости от доступных данных и задачи, можно выбрать наиболее подходящий способ и решить задачу эффективно и точно.
Определение высоты трапеции по используемой формуле
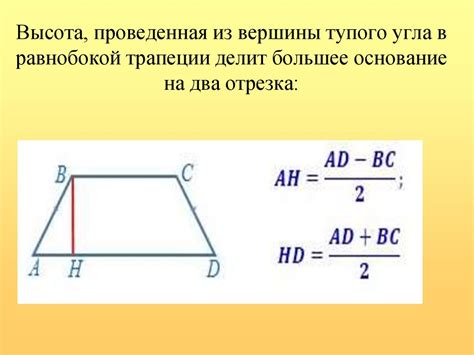
Мы рассмотрим метод, который позволяет найти высоту трапеции, используя специальную формулу и заданные основания. Этот метод основан на принципе нахождения перпендикуляра к основаниям, который называется высотой трапеции. Мы разберем формулу, которая позволяет нам вычислить эту высоту, и предоставим примеры для лучшего понимания.
Формула для определения высоты трапеции:
Для определения высоты трапеции необходимо знать длину обоих оснований трапеции и расстояние между ними. Формула, которая используется для вычисления высоты трапеции, имеет следующий вид:
высота = 2 * площадь / (основание_1 + основание_2)
В этой формуле, площадь трапеции вычисляется как половина произведения суммы оснований и высоты на расстояние между основаниями:
площадь = 0.5 * (основание_1 + основание_2) * расстояние_между_основаниями
Подставив значение площади из второй формулы в первую формулу, мы можем найти высоту трапеции.
Давайте рассмотрим пример, чтобы продемонстрировать этот метод.
Использование теоремы Пифагора для расчета вертикальной высоты четырехугольника

В трапеции с известными основаниями и углом, смежным с вертикальной стороной, можно построить прямоугольный треугольник, где одна из катетов - это вертикальная высота трапеции. Таким образом, используя теорему Пифагора, можно вычислить длину вертикальной высоты трапеции.
| Известные величины: | Длина одного основания трапеции | Длина другого основания трапеции | Величина угла, смежного с вертикальной стороной |
|---|---|---|---|
| Обозначение: | a | b | α |
Для вычисления высоты трапеции, сначала находим длину гипотенузы прямоугольного треугольника по формуле c = √(a² + b²). Затем, с помощью формулы h = c * sin(α), где h - высота трапеции, α - величина угла, смежного с вертикальной стороной, можем определить искомую высоту.
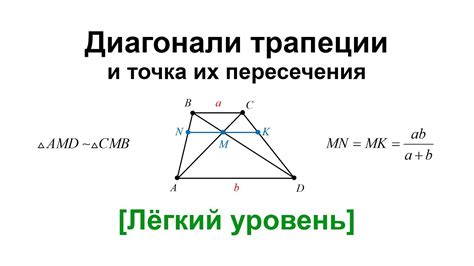
Расчет высоты трапеции через диагональ и основания
| Метод | Формула |
|---|---|
| Метод подобных треугольников | h = (d * √(a + b) ) / √(a - b) |
| Метод площадей | h = (2 * S) / (a + b) |
Первый метод использует принцип подобия треугольников для определения высоты трапеции. Путем вычисления соотношения длин сторон треугольников, полученных из оснований и диагонали, мы можем найти значение высоты.
Второй метод основан на равенстве площадей фигур, образованных основаниями трапеции, ее высотой и диагональю. Подставив известные значения оснований и диагонали в формулу, мы можем найти высоту трапеции.
Геометрическая конструкция для вычисления высоты трапеции: еще один подход в решении задачи

Рассмотрим интересный подход к определению высоты трапеции, который основан на геометрической конструкции. Вместо использования общеизвестных методов и формул, предлагается использовать геометрические принципы для получения аккуратного и точного решения.
Применение данной геометрической конструкции позволяет визуализировать процесс в определении высоты трапеции и при этом избежать использования сложных математических выкладок. Важно отметить, что данный подход является дополнительным инструментом и может быть особенно полезен для учащихся и тех, кто предпочитает более наглядные методы решения задач.
Для проведения геометрической конструкции мы используем таблицу, которая позволяет ясно видеть связь между различными параметрами трапеции. Используя таблицу, мы можем ввести синонимы, которые помогут нам избежать повторения одних и тех же терминов.
Процесс геометрической конструкции включает последовательность шагов, в которых мы создаем вспомогательные фигуры, проводим линии и определяем взаимосвязи между элементами. Основная идея состоит в том, чтобы использовать уже известные параметры трапеции для определения высоты визуально, без необходимости сложных вычислений.
| Известные параметры трапеции | Неизвестные параметры трапеции |
|---|---|
| Основания трапеции | Высота трапеции |
| Диагонали трапеции | |
| Углы трапеции |
Геометрическая конструкция позволяет исследовать различные аспекты трапеции, учитывая имеющуюся информацию. Она может быть использована как дополнение к классическим методам и формулам, предоставляя дополнительные инструменты для нахождения высоты трапеции.
Предлагаемый подход удобен тем, что не требует особых математических навыков и может быть использован различными категориями людей для более понятного решения задачи. Применение геометрической конструкции дает возможность не только определить высоту трапеции, но и лучше понять ее свойства и взаимосвязи с другими элементами, что может быть полезно в дальнейшем обучении геометрии.
Использование сходства треугольников для определения высоты трапеции
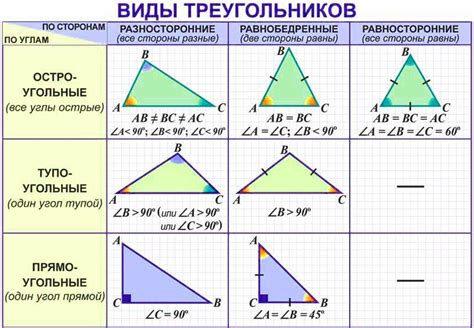
В данном разделе мы рассмотрим метод, основанный на сходстве треугольников, который позволяет определить высоту трапеции по известным параметрам без использования специальных формул и методов.
Сходство треугольников - это свойство, которое позволяет устанавливать соответствие между двумя треугольниками на основе их подобия. При наличии подобных треугольников, соответствующие стороны треугольников пропорциональны, что позволяет использовать эту связь для нахождения неизвестных значений.
Чтобы определить высоту трапеции с помощью сходства треугольников, необходимо построить подобные треугольники на основе известных параметров трапеции, таких как длины оснований и длины боковых сторон. Затем, используя полученные пропорции, можно вывести уравнение для определения высоты.
Теорема о пропорциональности боковых сторон трапеции: ключ к определению высоты
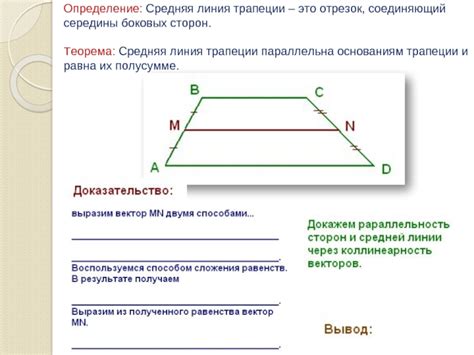
Теорема о пропорциональности боковых сторон трапеции: если две боковые стороны трапеции делятся их средней линией в одном и том же отношении, то они пропорциональны.
Иными словами, если мы знаем отношение, в котором боковые стороны делятся средней линией трапеции, мы можем использовать эту информацию для определения ее высоты. Высота трапеции является перпендикуляром, опущенным из одного из оснований на противоположную сторону, поэтому теорема о пропорциональности боковых сторон предоставляет нам ключевую информацию, необходимую для ее расчета.
Пример: Предположим, что известно, что боковые стороны трапеции делятся средней линией в отношении 2:3. Тогда мы можем использовать эту информацию для определения высоты трапеции. Пусть высота трапеции обозначается буквой "h". Поскольку отношение, в котором боковые стороны делятся средней линией, равно 2:3, мы можем записать соответствующее уравнение:
2/3 = h / (основание1 + основание2)
Используя это уравнение, мы можем рассчитать значение высоты трапеции, зная значения оснований и отношение, в котором боковые стороны делятся средней линией.
Расчет высоты трапеции на основе соотношения площадей
В данном разделе мы рассмотрим уникальный подход к определению высоты трапеции, основанный на соотношении площадей. Этот метод позволяет найти нужную величину без использования стандартных формул и оснований.
Идея состоит в том, чтобы использовать связь между площадями различных фигур, в которые можно разбить трапецию. Используя это соотношение, мы сможем выразить высоту трапеции через известные параметры, такие как длины оснований, углы и др.
Одним из способов применения этого подхода является разбиение трапеции на треугольники и прямоугольники. Затем, рассматривая площади данных фигур в соотношении друг к другу, мы можем получить формулу для вычисления высоты трапеции.
Кроме того, существуют и другие способы применения соотношения площадей для нахождения высоты трапеции. Например, мы можем использовать площадь прямоугольника, вписанного в трапецию, и площадь самой трапеции для получения соотношения, которое позволяет найти высоту.
Важно понимать, что данная методика не является основной формулой для определения высоты трапеции, однако она может быть полезна в определенных ситуациях, когда другие методы не применимы или результат нужно проверить. Поэтому рекомендуется учитывать этот подход при изучении и выполнении задач на тему нахождения высоты трапеции.
Практическое применение различных приемов для определения вертикали между реперными пунктами трапеции

При работе с неравнобедренными трапециями или при отсутствии прямоугольных известных опорных точек, для определения высоты трапеции можно использовать разнообразные методы, которые основаны на применении геодезических приемов и формул. Эти методы позволяют с высокой точностью определить вертикальные расстояния между пунктами трапеции.
Для практического применения методов определения высоты трапеции можно использовать таблицу, в которой указываются известные основания, углы между основаниями и прилегающими сторонами, а также методы, обеспечивающие определение вертикальных расстояний. Данная таблица помогает геодезистам выбрать наиболее подходящий метод для определения высоты трапеции в конкретных условиях выполнения работ.
Для определения высоты трапеции в геодезии широко применяются такие методы, как методы равных оснований, методы подобия трапеций или метод параллельных линий. Каждый из этих методов обеспечивает точное определение вертикального расстояния между реперными точками трапеции, независимо от формы и размера неизвестного сегмента.
| Метод | Описание | Преимущества | Недостатки |
|---|---|---|---|
| Метод равных оснований | Использует соотношения между треугольниками внутри трапеции | Прост в применении | Ограниченная применимость |
| Метод подобия трапеций | Использует свойства подобных фигур | Применим в любых условиях | Требует точных измерений углов и сторон |
| Метод параллельных линий | Определение высоты через параллельные линии на смежных сторонах | Прост в использовании | Может быть ограничено наличием параллельных сторон |
Практическое применение методов определения высоты трапеции позволяет геодезистам эффективно выполнять измерения и определение вертикальных расстояний в различных геодезических задачах. Комбинирование и выбор наиболее подходящего метода в зависимости от условий работы обеспечивает достоверные результаты и повышает точность позиционирования и измерения высот.
Вопрос-ответ

Как определить высоту трапеции по известным основаниям и площади?
Для определения высоты трапеции по известным основаниям и площади существует следующая формула: h = (2 * S) / (a + b), где h - высота трапеции, S - площадь трапеции, a и b - длины оснований. Подставляя известные значения в формулу, можно определить высоту трапеции.
Как определить высоту трапеции по известным основаниям и углу при основании?
Если известны основания трапеции и угол при одном из них, то высоту можно определить с помощью тригонометрических функций. Для этого используют формулу: h = (b - a) * tan(α), где h - высота трапеции, a и b - длины оснований, α - угол при основании. Подставив известные значения в формулу, можно определить высоту.
Как определить высоту трапеции по известным диагоналям и углу между ними?
Для определения высоты трапеции по известным диагоналям и углу между ними можно использовать формулу: h = d1 * d2 * sin(α) / (2 * S), где h - высота трапеции, d1 и d2 - длины диагоналей, α - угол между диагоналями, S - площадь трапеции. Подставив известные значения в формулу, можно определить высоту.
Как определить высоту трапеции по известным боковым сторонам и углу между ними?
Если известны боковые стороны трапеции и угол между ними, то высоту можно определить с помощью тригонометрической функции. Для этого используют формулу: h = a * sin(α), где h - высота трапеции, a - длина одной из боковых сторон, α - угол между боковыми сторонами. Подставив известные значения в формулу, можно определить высоту.
Как определить высоту трапеции по известному периметру и сумме оснований?
Если известны периметр и сумма оснований трапеции, то высоту можно определить с помощью следующей формулы: h = √(P^2 - 16S^2) / (2 * (a + b)), где h - высота трапеции, P - периметр, S - площадь, a и b - длины оснований. Подставив известные значения в формулу, можно определить высоту.
Как определить высоту трапеции по известным основаниям?
Для определения высоты трапеции по известным основаниям можно использовать несколько методов. Один из наиболее простых способов - использование формулы, где высота равна произведению оснований, деленному на сумму этих оснований, умноженную на половину диагонали трапеции. Другой способ - использование подобия треугольников. Если известны основания и параллельные им стороны, то можно составить пропорцию между высотой и одной из сторон, и решив ее, определить высоту трапеции.
Какие еще могут быть методы и формулы для определения высоты трапеции по известным основаниям?
Помимо уже упомянутых методов, существуют и другие формулы для определения высоты трапеции по известным основаниям. Например, можно использовать формулу для нахождения площади трапеции, в которой высота является неизвестной. Решив данную формулу относительно высоты, можно определить ее значение. Также, существуют специальные теоремы, связанные с трапециями, например, теорема Пифагора для трапеции, которая позволяет найти высоту, зная длину диагоналей и высоту прямоугольника, который можно вписать в данную трапецию.



