Когда мы имеем дело с числами, существует множество способов и методов для их сложения. Один из таких методов - сложение двоичных чисел. В данной статье мы рассмотрим конкретный практический пример сложения двух чисел в двоичной системе счисления, а именно чисел 11002 и 1012.
Перед тем, как приступить к решению задачи, необходимо разобраться в основных принципах двоичной системы счисления. В двоичной системе числа представляются комбинацией двух цифр: 0 и 1. В отличие от десятичной системы счисления, в которой каждая цифра имеет некоторое значение, в двоичной системе счисления каждая цифра обозначает степень числа 2.
Для сложения двух двоичных чисел необходимо сложить каждую пару соответствующих цифр по правилам сложения в двоичной системе счисления. Если сумма двух цифр превышает 1, то в результате сложения мы получаем 0 и перенос единицы на следующий разряд. В противном случае, если сумма цифр равна 1, то в результате получаем 1 без переноса. По мере продвижения от младших разрядов к старшим осуществляется сложение цифр и учет возможного переноса.
Основы и практические примеры сложения двоичных чисел

Основы сложения двоичных чисел
Двоичная система счисления использует только два символа - 0 и 1, что отражает присутствие или отсутствие сигнала в электронных компонентах. Для сложения двух двоичных чисел следует придерживаться подобных правил, как при сложении десятичных чисел. Дополнительными правилами являются:
0 + 0 = 0,
0 + 1 = 1,
1 + 0 = 1,
1 + 1 = 10.
Практический пример
Для наглядности рассмотрим пример сложения двух двоичных чисел: 1101 и 101. Начнем с самого младшего разряда, где сумма будет 1, а в разряде перенесется 0. Далее, в следующем разряде имеем две единицы и разряд переноса, что дает в результате 10 в этом разряде и перенос в разряд старше. В конечном итоге получим результат 10010.
Раздел: Основы двоичной системы счисления и ее применение для математических операций
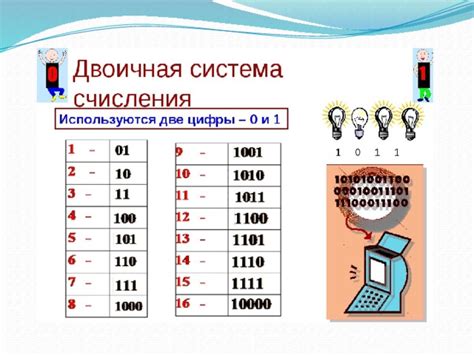
В данном разделе мы рассмотрим основные принципы двоичной системы счисления, ее структуру и способы применения для сложения чисел. Двоичная система, также известная как система счисления по основанию 2, широко используется в современных компьютерных технологиях. Ее применение позволяет эффективно представлять и оперировать с числами и данными в цифровой форме.
Двоичная система счисления основана на использовании двух цифр: 0 и 1. Каждая позиция числа в двоичной системе обозначает степень числа 2. Например, 1010 в двоичной системе счисления представляет собой число, равное 1*2^3 + 0*2^2 + 1*2^1 + 0*2^0 = 10.
Когда необходимо выполнить сложение двоичных чисел, используется специальный алгоритм. Учитывая, что каждая цифра в двоичной системе счисления может иметь только два значения (0 или 1), при сложении двух цифр возможны три сценария: 0 + 0 = 0, 1 + 0 = 1 и 1 + 1 = 10 (или 0 с переносом). Для складывания чисел, каждая позиция справа налево суммируется с учетом переноса, если таковой имеется, и полученный результат записывается в новую позицию. В конечном итоге получается сумма двух чисел в двоичной системе счисления.
Таким образом, использование двоичной системы счисления позволяет эффективно выполнять сложение чисел и проводить различные операции с данными в цифровом виде. Понимание принципов двоичной системы является важным для работы с компьютерными технологиями и программирования. Это обобщенное понимание позволяет нам более глубоко понять процесс сложения двух двоичных чисел и применять его практически в различных областях.
Значение сложения двоичных чисел в компьютерных науках

Операция сложения двоичных чисел имеет огромное значение в сфере компьютерных наук. Эта операция позволяет комбинировать двоичные числа для выполнения различных вычислительных задач и обеспечивает основу для работы с цифровой информацией.
Продолжительное использование сложения двоичных чисел в компьютерных науках объясняется его эффективностью и простотой. Эта операция является основной строительной единицей для выполнения более сложных математических операций, таких как умножение, деление и другие.
Сложение двоичных чисел позволяет представлять и обрабатывать информацию в виде битов, которые являются основными компонентами цифровых данных. Благодаря этому, компьютеры могут обрабатывать огромные объемы информации с высокой скоростью и точностью.
При сложении двоичных чисел выполняются простые операции с битами, такие как сложение без переноса и сложение с переносом. Эти операции позволяют комбинировать и объединять двоичные числа, что открывает двери к выполнению разнообразных алгоритмов и задач, связанных с обработкой числовых данных.
Более того, сложение двоичных чисел позволяет работать с логическими операциями, такими как логическое И, логическое ИЛИ и логическое исключающее ИЛИ. Это имеет важное значение для разработки и программирования, поскольку логические операции широко применяются в процессе принятия решений и управления данными в компьютерных системах.
Таким образом, сложение двоичных чисел является неотъемлемой частью компьютерных наук и обеспечивает надежную основу для работы с цифровыми данными. Эта операция способствует эффективной обработке информации и позволяет создавать сложные алгоритмы, которые делают вычислительные задачи выполнимыми.
Основные принципы операции сложения в двоичной системе

1. Сложение одиночных разрядов: Каждый разряд двоичного числа складывается независимо от других разрядов. При сложении двух разрядов, для получения результата необходимо учесть характеристику каждого из них, а именно наличие или отсутствие переноса.
2. Обработка переносов: Если сложение двух разрядов приводит к переносу, то этот перенос необходимо учесть при сложении следующих разрядов. В случае, если есть перенос после сложения разрядов, он записывается в следующий разряд результата.
3. Учет старшего разряда: При сложении двух двоичных чисел важно учесть, что результирующий разряд может оказаться большим, чем количество разрядов у исходных чисел. В случае, если старший разряд результата превышает установленное количество разрядов, результирующее число может быть больше исходных чисел.
Основные правила сложения двоичных чисел позволяют выполнять данную операцию в системе счисления на уровне разрядов. При сложении цифр в каждом разряде важно учитывать переносы и возможное превышение количества разрядов. Знание и понимание этих правил позволяют осуществлять сложение двоичных чисел правильно и без ошибок.
Шаг за шагом: процесс сложения двух двоичных чисел
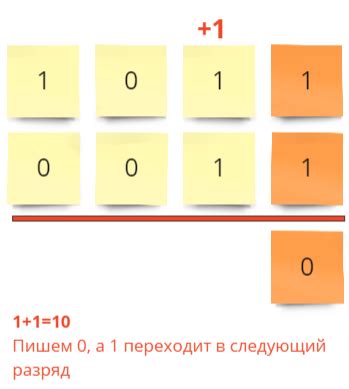
В данном разделе мы рассмотрим пошаговый процесс сложения двух двоичных чисел. Мы изучим, как сложить числа 11002 и 1012 и получить их сумму. Процесс будет разделен на несколько этапов для лучшего понимания.
Первым шагом является выравнивание чисел, чтобы их разряды совпадали. Поскольку двоичные числа имеют основание 2, каждому разряду назначается определенная степень числа 2. Например, самый правый разряд - это 2^0, следующий - 2^1, затем 2^2 и так далее.
Для выполнения сложения начинаем с самого правого разряда и перемещаемся влево. Если в каждом разряде у нас есть две единицы, мы записываем 0 и переносим один разряд влево. Если есть две единицы и перенос, мы записываем 1 и также переносим один разряд влево. Если сумма разряда и переноса равна 1, мы записываем 1 без переноса. И если сумма равна 0, мы записываем 0 без переноса.
Продолжаем сложение, повторяя эти шаги для каждого разряда до самого левого. Если после сложения остается последний перенос, мы записываем его слева от полученного результата.
Применяя описанный процесс к числам 11002 и 1012, мы получим сумму этих двух двоичных чисел.
| Разряд | 1-е число (1100) | 2-е число (101) | Результат | Перенос |
|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 1 |
| 2 | 1 | 0 | 1 | 1 |
| 3 | 0 | 1 | 1 | 0 |
| 4 | 1 | 0 | 0 | 1 |
| 5 | 0 | - | 1 | 0 |
В результате сложения двоичных чисел 11002 и 1012 мы получим число 10110.
Перенос разрядов при сложении двоичных чисел

Умение корректно переносить разряды играет важную роль в процессе сложения двоичных чисел. При сложении таких чисел могут возникнуть ситуации, когда сумма разрядов превышает двоичную систему счисления, и необходимо выполнить перенос единицы в старший разряд.
Для правильного переноса разрядов необходимо учесть следующие моменты:
- Сложение единицы и нуля: Если слагаемые в разряде дают сумму 1 и 0, то получается 1 без переноса.
- Сложение двух нулей: Если слагаемые в разряде дают сумму 0 и 0, то получается 0 без переноса.
- Сложение двух единиц: Если слагаемые в разряде дают сумму 1 и 1, то необходимо выполнить перенос единицы в следующий более старший разряд.
Перенос единицы происходит из младшего разряда в старший. При переносе следует учесть заранее заданный порядок, чтобы не возникло путаницы в результате сложения. Таким образом, правильное выполнение переноса разрядов обеспечит точность при сложении двоичных чисел и предотвратит ошибки.
Применение задачи по сложению двоичных чисел для лучшего понимания процесса
Разберем практический пример сложения двоичных чисел, который поможет улучшить наше понимание процесса и основных принципов, лежащих в его основе.
Изучение основных операций на двоичных числах не только позволяет нам понять принципы работы компьютерных систем, но и развивает навыки логического мышления и алгоритмического мышления. Одной из самых фундаментальных операций на двоичных числах является сложение.
Для лучшего понимания процесса сложения двоичных чисел мы рассмотрим конкретный пример. Мы возьмем два двоичных числа и применим наши знания о базовых правилах сложения, таких как сложение по столбикам и перенос разрядов.
В процессе решения задачи, мы будем шаг за шагом анализировать каждый бит числа и применять необходимые операции сложения, переноса и записи результата. Таким образом, мы сможем лучше осознать каждый шаг и взаимосвязь между операциями.
Итак, практический пример по сложению двоичных чисел поможет нам не только усвоить базовые правила выполнения операции, но и улучшит наше понимание процесса и умение применять его на практике.
Проверка корректности сложения двух чисел в двоичной системе счисления

В данном разделе рассматривается методика проверки правильности сложения двух чисел в двоичной системе счисления. Для достижения корректного результата требуется выполнить ряд шагов, которые обеспечат точность процесса сложения.
Одним из первых шагов является проверка наличия прямого переноса при сложении двух двоичных чисел. При наличии переноса с предыдущего разряда необходимо произвести его учет и добавить к полученной сумме. Данная операция проводится до тех пор, пока перенос существует.
Далее следует убедиться, что сложение чисел производится с правильными разрядами. Для этого рекомендуется использовать таблицу, которая позволяет визуально представить процесс сложения и убедиться, что количество и правильность разрядов учтены.
Итак, проверка правильности сложения двух двоичных чисел состоит из нескольких шагов: проверка наличия переноса, правильность разрядов и сравнение полученной суммы с результатом сложения чисел в прямом направлении. Соблюдение данных шагов гарантирует точность сложения и отсутствие ошибок.
| Перенос | Разряды | Результат |
|---|---|---|
| 0 | 0 + 0 | 0 |
| 0 | 0 + 1 | 1 |
| 1 | 0 + 1 | 0 |
| 1 | 1 + 1 | 1 |
Решение сложного задания: операция сложения двух бинарных чисел с разной длиной

В математике существует операция сложения двоичных чисел, которая позволяет суммировать числа, представленные в двоичной системе счисления. В данном разделе рассмотрим методику сложения двух двоичных чисел, учитывая случай, когда числа имеют различную длину.
Предположим у нас имеются два двоичных числа, которые необходимо сложить: число A и число B. Число A может содержать больше или меньше бит, чем число B, и наша задача - получить результат их сложения. Для этого требуется реализовать алгоритм, который позволит учесть и обработать различия в длине чисел A и B.
Для начала нам необходимо выравнять числа по длине. Для этого можно добавить нули перед числом, имеющим меньшую длину. Например, пусть число A имеет длину 6 бит, а число B имеет длину 4 бита. Чтобы выровнять их по длине, перед числом B следует добавить два нулевых бита, чтобы оба числа имели одинаковую длину.
После выравнивания длины чисел, мы можем приступить к их сложению бит за битом. Начиная с крайнего правого бита (наименее значимого разряда), мы складываем соответствующие биты чисел A и B, а также дополнительный бит, который может появиться при переносе единицы на предыдущий разряд. Результат сложения записывается в новое число C.
В случае, когда сумма битов превышает 1, возникает перенос, который должен быть учтен при сложении следующих разрядов. Этот перенос сохраняется в дополнительном бите и используется при сложении следующего разряда. В случае, когда количество разрядов числа A и B одинаковое, сложение выполняется от крайнего правого разряда к следующему разряду слева. Если дополнительный бит остается после сложения всех разрядов, он также должен быть учтен и добавлен в результат.
Таким образом, решая задание по сложению двух двоичных чисел с различной длиной, необходимо выравнять числа по длине, сложить их разряды, учитывать возможные переносы и дополнительные биты. Это позволит получить правильный результат исходной операции сложения двух двоичных чисел.
Преимущества использования двоичной системы счисления в компьютерной арифметике

Применение двоичной системы счисления обладает рядом преимуществ. Во-первых, двоичное представление чисел позволяет сократить объем информации, необходимый для хранения и передачи данных. Это особенно важно в сфере компьютерной техники, где сохранение ресурсов и обработка больших объемов информации являются ключевыми задачами.
Во-вторых, двоичная система счисления обеспечивает простоту и эффективность выполнения арифметических операций в компьютерах. Поскольку все операции в компьютере выполняются на уровне электрических сигналов, использование двуичной системы счисления позволяет легко и надежно производить сложение, вычитание, умножение и деление чисел. Это обеспечивает быстроту и точность вычислительных процессов.
Еще одним преимуществом двоичной системы счисления является ее универсальность и совместимость с компьютерной техникой. Все современные компьютерные системы используют двоичный код в своей работе, и поэтому представление и обработка данных в двоичном формате позволяет легко интегрировать различные компоненты и программное обеспечение.
Таким образом, применение двоичной системы счисления в компьютерной арифметике обеспечивает экономию ресурсов, быстроту и точность вычислительных процессов, а также облегчает интеграцию компонентов и программ в компьютерных системах.
Вопрос-ответ

Как сложить два двоичных числа 11002 и 1012?
Для сложения двоичных чисел 11002 и 1012 сначала выравниваем их по разрядам, добавляя в начало числа нули, если нужно. Получаем 011002 и 001012. Затем складываем разряды, начиная справа: 0+0=0, 1+0=1, 1+1=10 (записываем 0 и переносим 1), 0+0+1=1. Получаем результат: 100102. Еще добавляем перенос, если он есть. В данном случае переноса не возникло. Итого, сумма двоичных чисел 11002 и 1012 равна 100102.
Как происходит сложение двоичных чисел в данном примере?
В данном примере сложение двоичных чисел 11002 и 1012 происходит путем поэтапного сложения разрядов. Сначала числа выравниваются по разрядам, добавляя в начало числа нули, если нужно. Затем складываются разряды, начиная справа. Если при сложении разрядов получается число больше 1, то записывается только остаток от деления на 2, а единица переносится на следующий разряд. При этом результат сложения каждого разряда записывается справа налево. Если после сложения всех разрядов остается перенос, его также нужно учесть в итоговой сумме. В данном примере, результат сложения двоичных чисел 11002 и 1012 получается равным 100102.
Можете подробнее объяснить, как получается результат сложения двоичных чисел 11002 и 1012?
Конечно! При сложении двоичных чисел 11002 и 1012 сначала необходимо выравнить их по разрядам. В данном случае оба числа имеют 4 разряда, но в число 10 нужно добавить еще 2 нуля в начале. Получаем числа 011002 и 001012. Затем начинается пошаговое сложение разрядов, начиная справа. 0+0=0, 1+0=1, 1+1=10 (записываем 0 и переносим 1 в следующий разряд), 0+0+1=1. Таким образом, результат сложения двоичных чисел 11002 и 1012 равен 100102. В данном случае переноса не возникло, поэтому итоговый результат равен полученной сумме.



