Познакомимся с одним из самых важных аспектов геометрии - треугольником. У нас есть возможность раскрыть тонкости и секреты этой фигуры, сосредоточившись на одном из ее ключевых элементов - гипотенузе. Мы узнаем, как найти длину катетов треугольника, имея известную гипотенузу. Это знание является неотъемлемой частью решения множества задач, как в учебном процессе, так и в повседневной жизни.
Для начала мы погрузимся в атмосферу геометрического анализа, используя умение методически искать решение проблем, связанных с треугольником. Следуя определенной последовательности действий, мы сможем легко и точно определить длину двух катетов, основываясь только на значении гипотенузы. Открытие новых методов решения задач привнесет уверенность и опыт в наше понимание этой удивительной фигуры.
В ходе этого уникального путешествия мы обратимся к основным концепциям геометрии и разложим их на простые шаги. Мы ознакомимся с преимуществами и недостатками различных методов нахождения катетов, чтобы у нас была возможность выбрать наиболее подходящий подход в каждом конкретном случае. Результаты наших исследований позволят нам оценить сложность задач, связанных с треугольниками, и достичь новых горизонтов в практическом применении геометрии.
Основные понятия: гипотенуза и катеты

В этом разделе мы рассмотрим основные понятия, которые необходимо знать для понимания процесса нахождения катетов, когда известна гипотенуза. Понимание этих понятий поможет нам лучше ориентироваться в геометрических фигурах и решать задачи.
Гипотенуза - это главная сторона прямоугольного треугольника, которая является противолежащей прямому углу. Она служит основой для расчета катетов и имеет самую большую длину среди всех сторон треугольника.
Катеты - это две стороны прямоугольного треугольника, которые вместе с гипотенузой образуют прямой угол. Они являются более короткими сторонами треугольника и служат для подсчета его геометрических параметров.
Понимание гипотенузы и катетов является ключевым при решении задач на нахождение катетов по известной гипотенузе. Знание этих понятий позволяет нам правильно использовать соотношения и формулы для вычислений.
- Гипотенуза является наибольшей стороной треугольника.
- Катеты являются более короткими сторонами треугольника.
- Гипотенуза противолежит прямому углу.
- Катеты образуют прямой угол с гипотенузой.
Теперь, когда мы понимаем, что такое гипотенуза и катеты, мы готовы перейти к более подробному изучению темы нахождения катетов с известной гипотенузой.
Формула Пифагора и ее применение

Формула Пифагора основана на связи между длинами сторон прямоугольного треугольника и позволяет найти недостающие значения. В ее примитивной форме она выражает квадрат гипотенузы треугольника как сумму квадратов катетов. Это может быть полезно, когда известна только длина гипотенузы и необходимо найти длины катетов. Но насколько точно работает эта формула и как можно использовать ее для решения практических задач?
Нахождение катетов при заданной длине гипотенузы: шаги по поиску
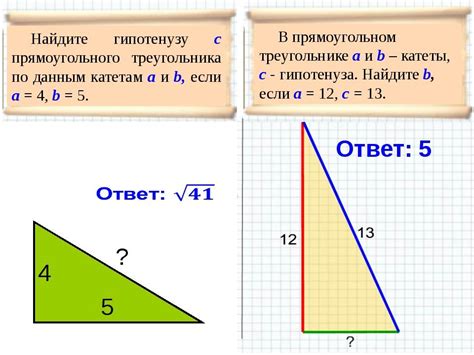
В этом разделе рассмотрим порядок действий, которые необходимо выполнить для определения длины катетов прямоугольного треугольника, если известна лишь длина гипотенузы. Без использования специфических терминов и определений объясним логику последовательных шагов, которые позволят нам решить данную задачу.
Шаг 1: Проверьте, что имеется треугольник с прямым углом и измерьте длину гипотенузы при помощи измерительного инструмента или линейки.
Шаг 2: Обозначьте неизвестные катеты буквами, используя, например, буквы "а" и "б".
Шаг 3: Сформулируйте теорему Пифагора, которая связывает гипотенузу и катеты. Это позволит нам построить уравнение, которое позволит найти значения катетов.
Шаг 4: Пользуясь формулой теоремы Пифагора, определите и составьте уравнение, связывающее гипотенузу и неизвестные катеты.
Шаг 5: Решите уравнение, найдя значения неизвестных катетов. Для этого можно использовать алгебраические операции, сокращая выражения и вычисляя значения.
Шаг 6: Проверьте полученные значения катетов, подставив их обратно в уравнение теоремы Пифагора и убедившись в его справедливости.
Конечно, существуют и другие способы нахождения катетов при известной гипотенузе, однако описанный в данном разделе подход является наиболее простым и доступным.
Пример 1: вычисление катетов с использованием формулы Пифагора

Для вычисления катетов треугольника с использованием формулы Пифагора, необходимо знать значение гипотенузы и, желательно, значения других сторон. На основе этих данных можно составить уравнения, которые позволяют найти значения катетов.
Изначально, можно обозначить длины катетов как a и b, а длину гипотенузы (известную в данном случае) - как c. По формуле Пифагора, для прямоугольного треугольника выполняется соотношение:
a2 + b2 = c2
Для упрощения расчетов и нахождения значений катетов можно использовать следующие шаги:
- Возьмите значение гипотенузы и возведите его в квадрат.
- Вычтите сумму квадратов известных сторон (если таковые имеются) из квадрата гипотенузы.
- Извлеките квадратный корень из полученного значения, чтобы найти значения каждого катета.
Теперь, используя эти шаги, можно приступить к вычислению катетов треугольника и получить точные значения, основанные на формуле Пифагора.
Пример 2: применение площадей треугольников для определения длин катетов
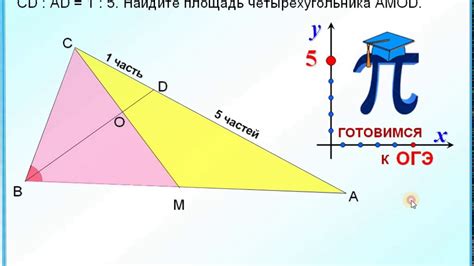
В этом разделе мы рассмотрим пример применения площадей треугольников для нахождения длин катетов. Методика основана на измерении площадей различных треугольников, образованных гипотенузой и катетами. После определения площадей всех треугольников, мы сможем использовать полученные значения для нахождения длин катетов.
В процессе данной методики мы рассмотрим различные шаги, включающие в себя выбор треугольника, измерение его площади и использование полученных данных для определения длин катетов. Такой подход позволяет получить точные значения исходя из геометрических принципов исследуемого треугольника.
- Выберите треугольник, состоящий из гипотенузы и одного из катетов.
- Измерьте длину выбранного катета и гипотенузы с использованием подходящих инструментов.
- Рассчитайте площадь треугольника, образованного выбранным катетом и гипотенузой, с помощью формулы площади треугольника.
- Повторите все предыдущие шаги для остальных катетов, образуя новые треугольники.
- Сравните площади треугольников и используйте их значения для определения пропорциональных длин катетов.
Применение площадей треугольников для определения катетов является эффективным методом, основанным на точности геометрических принципов. Следуя указанным шагам, вы сможете определить длины катетов с известной гипотенузой и улучшить свои навыки работы с треугольниками.
Пример 3: применение подобия треугольников для нахождения катетов
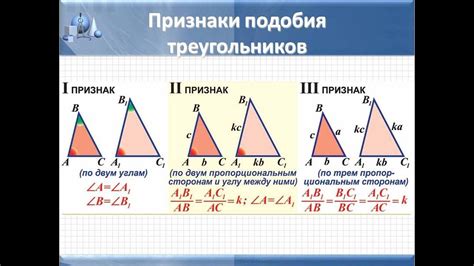
В данном примере мы рассмотрим использование подобия треугольников для определения значений катетов.
Подобие треугольников является важным свойством геометрических фигур, которое позволяет нам находить соответствующие стороны и углы. В случае треугольников, подобных друг другу, соотношение длин сторон и пропорции углов остаются одинаковыми. Это свойство можно использовать для определения значений катетов, если известна длина гипотенузы.
Давайте рассмотрим пример. Предположим, у нас есть треугольник с известной длиной гипотенузы, но неизвестными катетами. Мы можем использовать подобие треугольников и установить соотношение между сторонами треугольника, чтобы найти значения катетов. Для этого нам потребуется еще один треугольник, подобный исходному, но с известными катетами. Мы сможем установить пропорцию между сторонами треугольников и найти значения катетов.
Применение подобия треугольников для нахождения катетов может быть полезным при решении различных геометрических задач. Использование этой концепции позволяет нам упростить процесс нахождения неизвестных сторон и углов треугольников, сохраняя при этом точность результатов.
Решение задачи обратного треугольника
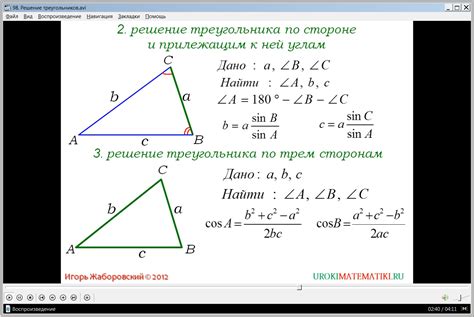
В этом разделе мы рассмотрим методику и подходы к решению задачи, которая заключается в нахождении катетов прямоугольного треугольника при известной длине гипотенузы. Мы описываем простые шаги и концепции, которые помогут вам успешно разрешить данную математическую задачу.
- Шаг 1: Определение известных данных - в первую очередь, необходимо установить, какие из данных уже известны вам. Таким образом, мы сможем использовать их для нахождения катетов.
- Шаг 2: Использование теоремы Пифагора - теорема Пифагора является ключевым инструментом для решения этой задачи. Мы разберем, как эту теорему применить и использовать для нахождения катетов треугольника.
- Шаг 3: Расчет и применение формулы - в этом шаге мы предоставим вам формулу, которая будет основой для расчета катетов при известной гипотенузе. Мы объясним, как использовать эту формулу и проведем несколько примеров для большего понимания.
- Шаг 4: Уточнение решения - в конечном итоге, мы рассмотрим расчеты, проведенные в предыдущем шаге, и дадим конкретные рекомендации, которые помогут вам уточнить ответ и провести дополнительные проверки.
С помощью этого подробного обзора вы сможете легко решать задачи на нахождение катетов с известной гипотенузой.
Практические советы для упрощения расчета катетов
При нахождении катетов, которые могут быть неизвестны, но известна гипотенуза, существует несколько полезных советов, которые могут упростить процесс вычислений. Ниже приведены практические рекомендации, которые помогут найти именно то, что вам нужно без излишних сложностей и запутанностей.
- Используйте теорему Пифагора
- Применяйте геометрические соотношения
- Упрощайте выражения и облегчайте расчеты
- Используйте элементарные функции
- Используйте готовые формулы и таблицы
Теорема Пифагора является основой для расчета сторон прямоугольного треугольника. Она гласит, что квадрат гипотенузы равен сумме квадратов катетов. Используя эту теорему, можно легко выразить один из катетов, если известна гипотенуза и второй катет.
Применение геометрических соотношений может оказаться полезным при вычислении катетов с известной гипотенузой. Например, используя подобные треугольники, можно выразить неизвестные стороны через известные и привести уравнение к удобному для решения виду.
Часто вычисления могут быть упрощены путем факторизации выражений, использования тривиальных соотношений и подстановки известных значений. Это позволяет сократить количество операций и сделать расчеты более простыми и быстрыми.
Расчет катетов может быть упрощен, если использовать элементарные функции, такие как корень квадратный или возведение в квадрат. Использование таких функций позволяет более компактно выразить результаты и упростить дальнейшие вычисления.
Существуют готовые формулы и таблицы, которые содержат соотношения между сторонами прямоугольных треугольников. Их использование позволяет быстро и точно вычислить катеты без необходимости проводить длительные выкладки и преобразования уравнений.
Применение полученных значений катетов в геометрических задачах

Полученные значения катетов могут быть использованы в различных геометрических задачах, где требуется определить длину отрезков, площадь фигур или углы между сторонами.
Определение длины отрезков: С использованием найденных катетов можно определить длину дополнительных отрезков, которые могут быть не указаны в условии задачи. Найденные значения катетов позволят вычислить длину этих отрезков и использовать их в дальнейших вычислениях.
Вычисление площади фигур: Найденные катеты можно использовать для вычисления площади треугольников, прямоугольников, квадратов и других геометрических фигур. Площадь треугольника, например, может быть вычислена по формуле S = (a * b) / 2, где a и b - найденные катеты.
Определение углов между сторонами: С помощью полученных значений катетов можно вычислить углы между сторонами треугольника или других геометрических фигур. Для этого можно воспользоваться тригонометрическими функциями, такими как синус, косинус, тангенс.
Вопрос-ответ

Как найти катеты треугольника, если известна длина гипотенузы?
Для нахождения катетов треугольника, если известна длина гипотенузы, можно использовать формулу Пифагора. Для этого нужно вычесть квадрат длины известного катета из квадрата длины гипотенузы и затем взять квадратный корень полученной разницы. Формула выглядит следующим образом: катет = √(гипотенуза^2 - известный катет^2).
Можно ли найти катеты треугольника, если известна длина гипотенузы в условных единицах?
Да, можно. Если длина гипотенузы известна в условных единицах, то длины катетов также будут выражены в тех же самых условных единицах. Для нахождения катетов треугольника можно использовать формулу Пифагора, которую я уже упомянул в предыдущем ответе. Важно помнить, что все величины должны быть выражены в одних и тех же единицах измерения.
Какие дополнительные данные нужны для нахождения катетов треугольника с известной гипотенузой?
Для нахождения катетов треугольника с известной гипотенузой нужно знать еще одну из сторон треугольника. Это может быть либо другой катет, либо значение угла между гипотенузой и одним из катетов. Без дополнительных данных нельзя однозначно определить значения катетов.
Есть ли другие способы нахождения катетов треугольника, кроме формулы Пифагора?
Да, существует несколько других способов нахождения катетов треугольника. Например, если известно значение угла между гипотенузой и одним из катетов, можно использовать тригонометрические функции (синус, косинус, тангенс) для вычисления значений катетов. Также можно использовать геометрические методы, если известны некоторые особые свойства треугольника.
Можно ли найти катеты треугольника только по длине гипотенузы?
Нет, нельзя однозначно найти катеты треугольника только по длине гипотенузы. Для нахождения катетов треугольника с известной гипотенузой также необходимо знать еще одну из сторон треугольника - либо другой катет, либо угол между гипотенузой и одним из катетов. Без дополнительной информации нельзя точно определить значения катетов.
Как найти катеты прямоугольного треугольника, если известна гипотенуза?
Для нахождения катетов прямоугольного треугольника, если известна гипотенуза, можно воспользоваться теоремой Пифагора. Согласно этой теореме, квадрат гипотенузы равен сумме квадратов катетов. Таким образом, если мы знаем длину гипотенузы и один из катетов, мы можем применить эту формулу, чтобы найти второй катет.



