Существует истинная загадка, которая заставляет нас задуматься: какое именно число пребывает в числовом промежутке до числа девятнадцать? В поисках ответа, мы окунемся в увлекательное исследование и попробуем раскрыть эту тайну с помощью логического анализа и детального анализа возможных вариантов. Ведь интересное историческое исследование заставляет нас не только познавать, но и вдохновляет на смелые размышления!
Прежде чем мы перейдем к описанию самого ответа на загадку, давайте оглядимся вокруг и узнаем, какие мысли и предположения возникают у нас в попытке найти число, находящееся в порядке своего возникновения до девятнадцатого. Сколько в нашей жизни чисел существует, обладающих своей маленькой частью семнадцатью? Будем ли мы сталкиваться с числами, которые меньше семнадцати, но больше двенадцати? Позвольте нам вступить в волшебный мир размышлений и вместе с вами задаться этими и другими увлекательными вопросами!
А теперь пора обратиться к самому ответу. Будучи на пути к разгадке, мы обнаружили нечто захватывающее и удивительное. Число, которое раскрывает тайну, находится всего на один шаг ближе к числу, названному нами ранее – особое число, которое внедряет в нашу реальность непостижимые законы и возможности. Это число, на самом деле, оказывается необычным, захватывающим, недосягаемым и вдохновляющим. Почувствуйте, как усиливается наш трепет исследователей, когда нашли то, что искали!
Концепция чисел и их взаимосвязи
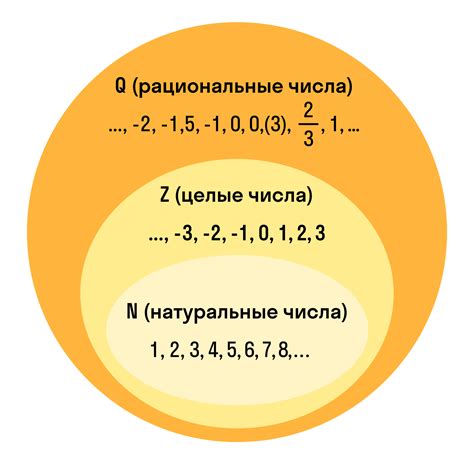
Взглянув на наше повседневное окружение, мы можем отметить, что существуют разные размеры и значения. Одно число может быть меньше другого. В теории чисел понятие "меньшее число" позволяет нам сравнивать числа и устанавливать их отношение. Несмотря на то, что мы не употребляем слово "меньше", важно понимать, что меньшее число обладает определенными свойствами, которые помогут нам проводить операции с числами и использовать их в различных математических задачах.
Для лучшего понимания концепции меньшего числа, мы рассмотрим его взаимосвязь с другими понятиями. Указав ряд синонимов и аналогий, мы поможем вам уловить суть и значение меньшего числа в контексте теории чисел. Определение меньшего числа - одна из важных составляющих нашего математического арсенала, которая позволяет нам систематизировать и структурировать числовые данные для их последующего использования в различных областях науки и повседневной жизни.
Понимание понятия "меньше" в математике
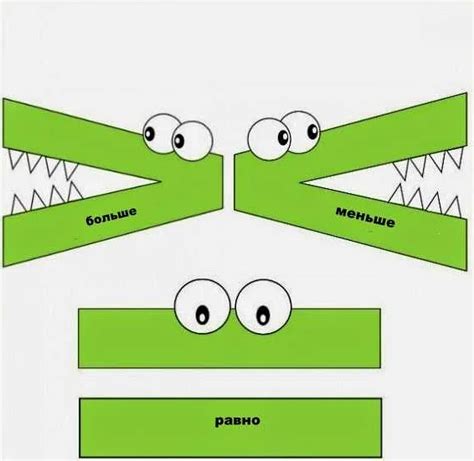
"Меньше" означает, что одно число находится на меньшем значении числовой шкалы по сравнению с другим числом. В математике используются различные способы обозначения отношения "меньше". Например, можно использовать знак "<", который обозначает, что число слева от знака меньше числа справа, или знак "≺", который также указывает на отношение "меньше".
При сравнении чисел важно учитывать их значения и порядок. Если число A меньше числа B, то A находится на числовой шкале перед B. Также важно помнить, что "меньше" - это относительное понятие. Для разных числовых систем и контекстов "меньше" может иметь разные значения.
- Понятие "меньше": обозначения и значения
- Порядок чисел и отношение "меньше"
- Сравнение чисел на числовой шкале
- Относительность понятия "меньше"
Понимание понятия "меньше" в математике является фундаментальным для проведения сравнений и решения различных задач.
Обзор натуральных чисел и их взаимоотношений

В данном разделе представлен обзор набора чисел, которые служат основой для измерения количества или порядка. Здесь мы рассмотрим основные характеристики натуральных чисел и принципы их взаимоотношений.
Натуральные числа - это положительные целые числа, которые используются для подсчета или упорядочивания объектов. Они включают в себя числа от одного и далее, и являются неотъемлемой частью математической нотации.
Отношения между натуральными числами позволяют устанавливать и сравнивать их величину или порядок. Рассмотрение отношений, таких как больше, меньше или равно, помогает нам сравнивать и классифицировать числа в соответствии с их значениями.
Используя математические операции и свойства, мы можем проводить операции над натуральными числами, такие как сложение, вычитание, умножение и деление. Эти операции дают нам возможность изменять и манипулировать числами, чтобы получать новые значения или устанавливать их взаимоотношения.
Раздел "Обзор натуральных чисел и их взаимоотношений" позволит вам более глубоко понять сущность натуральных чисел, их использование в математике и их значимость в повседневной жизни.
Способы определения меньшего числа из двух

В данном разделе рассмотрим различные подходы и методы для определения числа, которое имеет более низкое значение в паре чисел. Мы представим несколько способов, которые помогут нам сравнить и выбрать наименьшее число.
| Метод | Описание |
|---|---|
| Сравнение | Этот метод основан на прямом сравнении двух чисел с помощью операторов сравнения, таких как "больше", "меньше" или "равно". Исходя из результата сравнения, мы можем определить, какое число является наименьшим. |
| Абсолютное значение | Абсолютное значение числа играет ключевую роль при определении его относительного размера. Рассмотрим модуль каждого числа и сравним полученные значения, чтобы определить, какое из чисел имеет меньшую абсолютную величину. |
| Итеративное сравнение | В некоторых случаях у нас может быть несколько чисел, и нам нужно определить наименьшее число из них. Используя итеративный подход, пройдемся по всем числам и сравним их друг с другом, отвергая числа с большим значением, чтобы найти самое маленькое. |
Теперь, зная различные методы определения меньшего числа, вы сможете эффективно сравнивать и выбирать наиболее подходящие значения в различных ситуациях.
Графическое представление неравенств

В этом разделе рассмотрим способы визуализации неравенств и их графическое представление. Уникальные способы, которые помогут наглядно представить отношения между числами без использования прямой формулировки или числовых значений.
Мы погрузимся в мир символов, значков и графиков, чтобы исследовать, как неравенства между числами могут быть представлены визуально. Вместо простого использования чисел и математических сравнений, мы будем искать альтернативные пути для обозначения неравенств.
Воспользуемся разнообразными геометрическими фигурами, стрелками, полосами и другими символами, чтобы передать информацию о том, какое число является меньшим или большим в данном контексте.
Научимся интерпретировать эти графические представления и использовать их для более наглядного объяснения неравенств. Без использования обычных математических терминов или цифр, мы сможем передать суть неравенств, делая математику более доступной и интересной для всех.
Арифметические операции и сравнение чисел
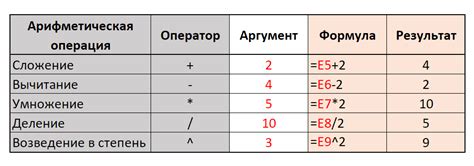
| Операция | Описание |
|---|---|
| Сложение | Узнаем сумму двух чисел путем их сложения. Результатом будет число, которое будет больше или меньше исходных в зависимости от значений. |
| Вычитание | Вычитаем одно число из другого и получаем разность. Если полученное значение положительное, то число, из которого производится вычитание, больше. В противном случае оно меньше. |
| Умножение | Умножение двух чисел дает нам произведение. Если произведение положительное, то оба числа имеют одинаковый знак и меньшего из них нет. Если произведение отрицательное, то число с отрицательным знаком является меньшим. |
| Деление | При делении одного числа на другое получаем частное. Если оба числа положительные, то меньшим будет делитель. Если одно из чисел отрицательное, то знак результата зависит от четности делителя. |
Кроме основных арифметических операций, мы рассмотрим и другие способы определения меньшего числа, такие как сравнение абсолютных значений, использования условных операторов и функций.
Используя эти знания, вы сможете легко определить, какое число меньше в различных ситуациях и упрощать свою работу с числами.
Применение теории чисел в реальной жизни

В современном мире, где математические принципы проникают во все сферы нашей жизни, теория чисел играет важную роль. Она помогает нам понять и анализировать различные явления, прогнозировать тренды и оптимизировать процессы.
Благодаря теории чисел мы можем рассчитывать сложности криптографических алгоритмов, которые защищают нашу информацию от несанкционированного доступа. Эта область математики также важна для разработки эффективных алгоритмов сжатия данных, которые позволяют нам экономить пространство на диске и быстро передавать информацию по сети.
Теория чисел также находит применение в финансовой аналитике. С помощью методов из этой области математики мы можем анализировать финансовые временные ряды, идентифицировать тренды и прогнозировать будущие цены на активы. Это позволяет нам принимать обоснованные инвестиционные решения и управлять рисками.
Наряду с этим, теория чисел играет важную роль в криптографии и безопасности информации. Методы из этой области помогают нам защищать данные от хакеров и создавать надежные системы аутентификации.
Также, теория чисел применяется в сетях передачи данных. Она позволяет нам эффективно решать проблемы связанные с распределением ключей, управлением ошибками и кодированием информации.
Таким образом, теория чисел является неотъемлемой частью наших жизней, она позволяет нам решать различные задачи с помощью математических принципов и методов. Знания этой области помогают нам лучше понимать и анализировать мир вокруг нас, оптимизировать процессы и принимать обоснованные решения.
Вопрос-ответ

Какое число меньше 19?
Число, которое меньше 19, это любое число, находящееся в промежутке между нулем и 19. Например, 10 или 15.
Можете ли вы назвать число, которое меньше 19?
Да, я могу назвать несколько чисел, которые меньше 19. Например, 10, 15, 5, 1 и т.д.
Какое число является наибольшим из чисел, меньших 19?
Наибольшее число, меньшее 19, это число 18. Все числа от 1 до 18 меньше 19, но 18 является самым большим в этом диапазоне.
Почему вопрос о том, какое число меньше 19 так популярен?
Возможно, вопрос о том, какое число меньше 19, является популярным, потому что 19 является числом, которое многим знакомо, и люди интересуются числами, которые меньше этого значения. Также это может быть связано с математическими задачами или играми, где нужно найти числа в определенном диапазоне.



