Разбор задач, связанных с глубоким пониманием структуры матриц, неотъемлемая часть развития алгоритмов обработки данных. Однако всегда возникает вопрос: как точно определить ранг матрицы, чтобы получить полную картину и выявить ее математическую ценность? Мы представляем Вашему вниманию инновационную методику, основанную на анализе окаймляющих миноров.
Суть этого подхода заключается в определении уровня структурной значимости в виде элементарных множеств. Данный метод позволяет учесть важность каждого элемента матрицы и дать точную оценку ее ранга без лишних вычислений и сложных алгоритмов.
Роль ранга матрицы в линейной алгебре

Понимание роли ранга матрицы позволяет проводить исследования и решать различные задачи в области линейной алгебры. Ранг матрицы применяется в теории систем, численных методах, решении систем линейных уравнений и оценке оптимальности задач оптимизации. Зная ранг матрицы, можно выявить свойства данной матрицы, такие как ее полный или неполный ранг, и использовать данную информацию для определения ее характеристик.
Основополагающий факт состоит в том, что ранг матрицы является одним из фундаментальных параметров, которые описывают структуру линейного пространства, порожденного данной матрицей. Ранг матрицы также связан с понятиями идеала, системы линейных уравнений и пространственных разбиений. Поэтому, исследование ранга матрицы имеет жизненную важность в различных областях науки и техники.
Роль окаймляющих миноров в определении ранга матрицы

Подробное изучение окаймляющих миноров дает нам возможность установить связь между их порядками и рангом матрицы. С помощью этих миноров можно выявить наличие линейной зависимости, позволяющей установить, насколько "компактно" можно представить матрицу.
Учитывая, что окаймляющие миноры это подматрицы, образованные выбранными строками и столбцами, их анализ позволяет нам сократить количество операций для определения ранга матрицы. Процесс определения ранга матрицы с помощью окаймляющих миноров особенно полезен в случаях, когда матрица имеет большой размер или является разреженной.
Таким образом, изучение связи ранга матрицы с окаймляющими минорами является важным шагом в понимании структуры матрицы и дает возможность более эффективно работать с ней при вычислительных операциях.
Определение окаймляющих миноров и их роль в вычислении ранга матрицы

Окаймляющие миноры представляют собой специальные подматрицы, образованные выборкой определенных строк и столбцов из изначальной матрицы. Они играют важную роль в определении ранга матрицы и позволяют выявить взаимосвязи между элементами матрицы.
Ранг матрицы определяется как максимальное количество линейно независимых строк (столбцов) в данной матрице. Для определения ранга матрицы с помощью окаймляющих миноров необходимо выбрать все возможные подмножества ее строк (столбцов) и построить матрицы, составленные из данных подмножеств. Затем для каждой построенной матрицы вычисляются ее окаймляющие миноры. Ранг матрицы будет равен наибольшему порядку окаймляющего минора, который является ненулевым и отличается от нуля.
Окаймляющие миноры позволяют описать структуру матрицы и выявить ее свойства, такие как линейная зависимость между строками (столбцами) и связи между элементами. Они служат основой для определения ранга матрицы и находят применение во многих областях, таких как алгебра, линейная алгебра, теория графов и машинное обучение.
- Окаймляющие миноры помогают вычислить ранг матрицы и определить ее линейную независимость.
- Они позволяют выявить связи между элементами матрицы и описать ее структуру.
- Окаймляющие миноры являются основой для разработки эффективных алгоритмов в области линейной алгебры и машинного обучения.
- Использование окаймляющих миноров позволяет оптимизировать вычисления и сократить количество операций при работе с матрицами.
- Они находят применение в различных областях науки и техники, где требуется анализ и обработка данных в виде матриц.
Способы вычисления окаймляющих миноров

Этот раздел посвящен рассмотрению различных подходов и методик, которые позволяют находить окаймляющие миноры. Эти методы обеспечивают данные, необходимые для определения ранга матрицы, в частности в контексте использования окаймляющих миноров.
Первый способ, который мы рассмотрим, основывается на известной теореме о существовании окаймляющих миноров в матрице. Мы рассмотрим алгоритм, который позволяет находить эти миноры с использованием метода исключения Гаусса. Этот метод позволяет вычислить определенные участки матрицы, такие как главные диагонали и окаймляющие миноры, которые затем могут быть использованы для определения ранга матрицы.
Второй способ, который мы рассмотрим, основывается на применении метода взаимного вычета. Этот метод позволяет вычислить определенные комбинации окаймляющих миноров и представить их в виде элементарных матриц. Таким образом, можно определить ранг матрицы, используя элементарные преобразования и вычисления окаймляющих миноров.
Третий способ, который мы рассмотрим, основывается на применении метода Симплекс для линейного программирования. Этот метод позволяет найти направление роста окаймляющих миноров и их границ, что в конечном итоге позволяет определить ранг матрицы. Мы рассмотрим примеры, в которых метод Симплекс применяется для вычисления окаймляющих миноров и определения ранга матрицы.
- Рассмотрение различных подходов и методик для нахождения окаймляющих миноров
- Известная теорема о существовании окаймляющих миноров и алгоритм нахождения с использованием метода исключения Гаусса
- Применение метода взаимного вычета для вычисления комбинаций окаймляющих миноров
- Использование метода Симплекс для определения направления роста окаймляющих миноров и границ
Поиск ключевых подматриц для определения ранга матрицы
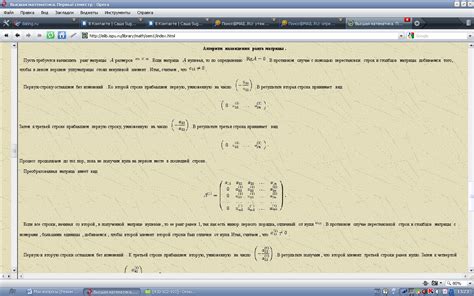
В данном разделе рассматриваются различные методы обнаружения и анализа окаймляющих миноров в матрице. Окаймляющие миноры представляют собой специальные подматрицы, созданные путем выбора определенных строк и столбцов из исходной матрицы.
Используя разные подходы и алгоритмы, можно выявить ключевые подматрицы, которые имеют важное значение для определения ранга исходной матрицы. Такие подматрицы позволяют выявить зависимости и структуру данных в матрице. Данная информация полезна в различных областях, включая линейную алгебру, теорию графов и геометрию.
Важно отметить, что существуют разные методы для поиска окаймляющих миноров. Один из подходов основан на применении элементарных преобразований к матрице, включая перестановки строк и столбцов, умножение строк на константу и сложение строк. Другой метод основан на использовании алгоритма Гаусса для приведения матрицы к улучшенному ступенчатому виду.
Кроме того, существуют итерационные методы поиска окаймляющих миноров, которые включают поэлементный анализ и проверку линейной независимости строк и столбцов. Эти методы могут быть полезны при работе с большими матрицами, где применение более традиционных алгоритмов может быть неэффективным.
- Метод 1: Применение элементарных преобразований
- Метод 2: Алгоритм Гаусса
- Метод 3: Итерационные подходы
Каждый из представленных методов имеет свои преимущества и недостатки, и выбор конкретного метода зависит от контекста и требований задачи.
Критерии вычисления ранга матрицы на основе окаймляющих миноров

Этот раздел посвящен анализу критериев, позволяющих определить ранг матрицы на основе окаймляющих миноров. Вместо прямого упоминания данных терминов, будут использованы синонимы для описания этих концепций.
- Матрица, которая представляет собой прямоугольную таблицу чисел, может быть исследована с точки зрения ее характеристик.
- Одной из таких характеристик является ранг матрицы, который отражает количество столбцов или строк, линейно независимых друг от друга.
- Для определения ранга матрицы с использованием окаймляющих миноров, центральным понятием становится понятие "базисных миноров".
- Базисные миноры формируются путем выбора некоторых строк и столбцов из исходной матрицы и создания новой матрицы, размерность которой меньше исходной.
- Анализ окаймляющих миноров и их отношений позволяет вычислить ранг матрицы и определить ее линейную независимость.
- При проведении анализа, используются определенные алгоритмы и методы, которые позволяют выявить наличие или отсутствие линейной зависимости.
- Окаймляющие миноры служат основным компонентом в данных методах и позволяют определить границы для принятия решения о ранге матрицы.
Таким образом, раздел "Критерии определения ранга матрицы с использованием окаймляющих миноров" рассматривает основные идеи и принципы, лежащие в основе данного подхода к определению ранга матрицы. Анализ окаймляющих миноров и их отношений играет ключевую роль в процессе вычисления ранга и определения линейной независимости матрицы.
Различные условия для вычисления числа линейно независимых строк или столбцов матрицы через границы ее подматриц

Существует несколько различных методов, позволяющих определить ранг матрицы с использованием окаймляющих миноров. Один из таких методов основан на вычислении числа линейно независимых строк или столбцов матрицы через границы ее подматриц. Определение ранга матрицы с помощью окаймляющих миноров позволяет получить информацию о ее линейной независимости и размерности пространства, порождаемого ее строками или столбцами.
Для определения ранга матрицы можно использовать границы подматриц различного размера. Например, в случае квадратной матрицы можно рассмотреть все ее подматрицы, начиная с подматриц размера 1x1 и заканчивая самой исходной матрицей. Подсчет числа линейно независимых строк или столбцов для каждой из этих подматриц позволит определить ранг исходной матрицы.
Также можно использовать другие схемы границ подматриц для определения ранга матрицы. Например, можно рассмотреть только подматрицы, граничащие с определенными строками или столбцами, или ограничиться только подматрицами с заданным количеством строк или столбцов. Каждая из этих схем может дать дополнительную информацию о ранге матрицы, позволяя выявить ее специфические свойства и особенности.
- Пример 1: Вычисление ранга матрицы через очередность удаления строк или столбцов.
- Пример 2: Определение ранга матрицы на основе миноров различного размера.
- Пример 3: Использование границ подматриц для определения ранга квадратной матрицы.
Примеры использования окаймляющих миноров для вычисления порядка матрицы

Первым примером будет рассмотрена матрица, которая задает систему линейных уравнений. Вычисление окаймляющих миноров данной матрицы позволит определить, сколько независимых уравнений в системе и какое количество переменных в системе. Это позволит, например, определить, можно ли найти единственное решение системы уравнений или же система имеет множество решений.
Вторым примером будет матрица, представляющая графическое изображение объекта. Рассмотрение окаймляющих миноров данной матрицы позволит определить, как много различных элементов содержится в изображении и насколько сложным является представление объекта. Используя данную информацию, можно, например, определить наличие определенных структурных элементов в изображении или сравнить сложность разных объектов.
Вопрос-ответ

Как определить ранг матрицы с помощью окаймляющих миноров?
Ранг матрицы можно определить с помощью окаймляющих миноров, которые получаются из исходной матрицы путем удаления одного или нескольких столбцов и строк. Ранг матрицы равен наибольшему порядку окаймляющего минора, который не равен нулю.
Какую роль играют окаймляющие миноры при определении ранга матрицы?
Окаймляющие миноры являются важным инструментом для определения ранга матрицы. Они позволяют нам выбирать подматрицы, удаляя один или несколько столбцов и строк, и вычислять определители этих подматриц. Ранг матрицы равен наибольшему порядку окаймляющего минора, который не равен нулю. Таким образом, окаймляющие миноры помогают нам определить, насколько матрица невырожденная и как много линейно независимых строк или столбцов в ней.
Могут ли окаймляющие миноры дать неверный результат при определении ранга матрицы?
Окаймляющие миноры не могут дать неверный результат, если выполняются все необходимые шаги правильно. Ранг матрицы определен как наибольший порядок окаймляющего минора, который не равен нулю. Окаймляющие миноры позволяют нам выбирать подматрицы и вычислять их определители. Если все шаги выполнены корректно, то окаймляющие миноры точно определят ранг матрицы.



