В геометрии структуры различных фигур подвергаются тщательному анализу. Одной из таких фигур является трапеция, которая обладает особым характером и уникальными свойствами. В данной статье мы сосредоточимся на исследовании методов определения углов трапеции при известных значениях сторон и средней линии. Этот анализ позволит нам лучше понять зависимости и соподчинения между основными элементами трапеции, что непременно найдет свое применение в области геометрии и строительства.
Цель нашего исследования заключается в том, чтобы обнаружить закономерности и законы, связывающие углы трапеции с ее сторонами и средней линией. Установление их взаимосвязи позволит нам углубить наши знания о трапеции и расширить понимание ее внутренних характеристик.
Изучение этой методики поможет нам при выполнении задач, связанных с построением и расчетами в геометрии. Также мы сможем применить наши знания на практике, например, в строительстве зданий, проектировании дорог или создании различных форм и конструкций. Это удобное средство для анализа и определения углов трапеции сделает нашу работу эффективнее и точнее, а также позволит сэкономить время при решении задач, требующих построения и измерения трапеций.
Определение углов трапеции: ключевые аспекты и принципы

В данном разделе рассматривается процесс определения углов фигуры, известной своей особенной формой, которую можно охарактеризовать как четырехугольник с двумя параллельными сторонами. Подробно анализируются главные принципы, позволяющие определить углы трапеции, используя различные характеристики и свойства данной фигуры.
Ключевые аспекты:
- Геометрические составляющие: представление о том, как фигура построена, где размещаются основные элементы, такие как стороны, углы, и как они соотносятся друг с другом.
- Теоремы и свойства трапеции: обзор известных математических утверждений, позволяющих найти взаимосвязь между углами трапеции и другими её характеристиками.
- Способы измерения: описание различных методик и инструментов, которые позволяют определить величину углов трапеции с высокой точностью и эффективностью.
Важно отметить, что нахождение углов трапеции получило широкое применение и значимость в различных областях, включая архитектуру, инженерные расчеты и геодезию. Понимание принципов и методик нахождения углов трапеции позволяет улучшить точность и достоверность результатов измерений и расчетов, а также обеспечивает возможность более глубокого изучения особенностей данной геометрической фигуры.
Понимание основных принципов и связей в изучении геометрии трапеции

Для того чтобы глубже разобраться в методах определения углов трапеции по ее сторонам и средней линии, необходимо понимать основные понятия, которые лежат в основе этой темы. В данном разделе мы рассмотрим ключевые определения и связи, которые помогут ученикам более четко представить себе суть изучаемого материала.
| Понятие | Определение |
|---|---|
| Трапеция | Геометрическая фигура с двумя параллельными сторонами, называемыми основаниями, и двумя непараллельными сторонами, называемыми боковыми сторонами. |
| Вершина | Точка пересечения боковых сторон трапеции. Всего в трапеции есть две вершины. |
| Угол | Фигура, образованная двумя сторонами, разделяющими общую точку, называемую вершиной угла. Углы трапеции могут быть как острыми, так и тупыми. |
| Базы | Основания трапеции, которые являются параллельными сторонами и находятся на противоположных концах фигуры. |
| Средняя линия | Отрезок, соединяющий середины боковых сторон трапеции и параллельный основаниям. Длина средней линии равна полусумме длин оснований. |
Понимая эти основы геометрии трапеции, можно более уверенно приступить к изучению методов нахождения ее углов по данным сторонам и средней линии. Определение основных понятий позволяет ученикам лучше воспринимать и анализировать геометрические задачи, связанные с трапецией, и делает процесс их решения более эффективным и точным.
Свойства трапеции
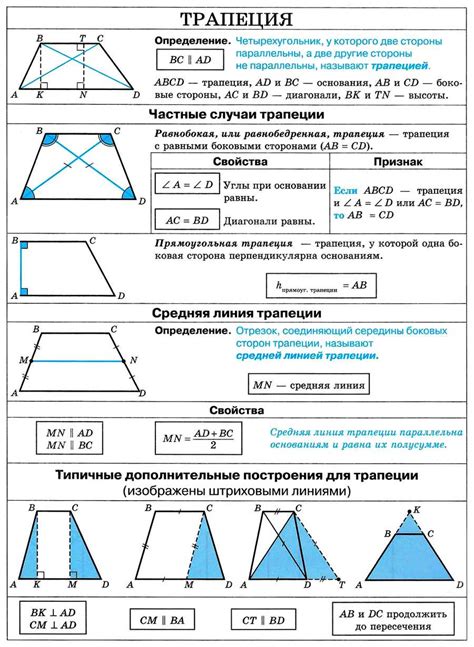
В данном разделе рассмотрим основные характеристики и свойства геометрической фигуры, которая обладает параллельными основаниями и боковыми сторонами разной длины.
| Свойство | Описание |
| 1. | Трапеция имеет две параллельные стороны, называемые основаниями. |
| 2. | Основания трапеции не пересекаются. |
| 3. | Две боковые стороны трапеции могут быть равны или неравны. |
| 4. | Сумма углов трапеции равна 360 градусов. |
| 5. | Боковые стороны трапеции перпендикулярны к ее основаниям. |
| 6. | Средняя линия трапеции является отрезком, соединяющим середины оснований. |
Изучение свойств трапеции позволяет более глубоко понять ее структуру и использовать их для решения различных геометрических задач. Наличие параллельных сторон и перпендикулярности боковых сторон обеспечивает определенные свойства углов и отношений между сторонами. Разбор и использование этих свойств является важным элементом при работе с трапецией в практическом применении.
Формула для определения средней прямой трапеции
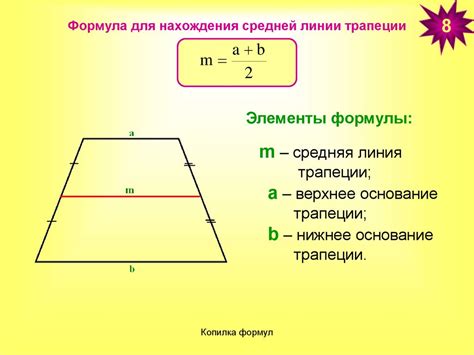
В данном разделе мы рассмотрим метод, позволяющий найти среднюю прямую трапеции без использования углов, сторон и понятия "нахождения".
Средняя прямая трапеция – это геометрическая фигура, имеющая свою специфическую форму и характерные свойства. Для ее определения существует формула, основанная на суммировании значений средних линий.
Средняя линия трапеции примыкает к длинным сторонам и делит их пополам. Используя данное свойство, мы можем определить среднюю линию, а затем найти среднюю прямую трапеции.
Формула для нахождения средней линии трапеции представлена в таблице ниже:
| Формула | Описание |
|---|---|
| l | Длина средней линии |
| a | Длина верхней основания |
| b | Длина нижней основания |
Таким образом, для определения средней прямой трапеции необходимо знать значения длин верхнего и нижнего оснований, а также применить указанную формулу для нахождения длины средней линии.
Определение углов трапеции по средней оси
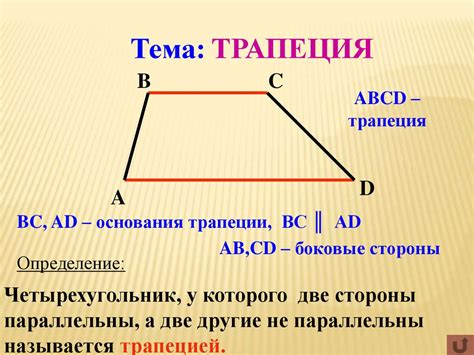
Для определения углов трапеции по средней оси можно использовать следующую методику:
- Измерьте длину средней оси с помощью прямой линейки или другого инструмента, точно определяющего размеры.
- Так как средняя ось трапеции является отрезком, соединяющим середины непарных сторон, ее длина будет равна полусумме длин этих сторон.
- Зная длины сторон, можно вычислить углы с помощью формул геометрии и тригонометрии, учитывая, что трапеция является выпуклым четырехугольником и угол на основании, противолежащий равным сторонам, будет равен.
Таким образом, определять углы трапеции по средней оси достаточно просто с использованием измерительных инструментов и знания основ геометрии. Этот метод позволяет точно определить углы фигуры и использовать их в решении различных геометрических задач.
Примеры успешного решения задач на определение углов трапеции
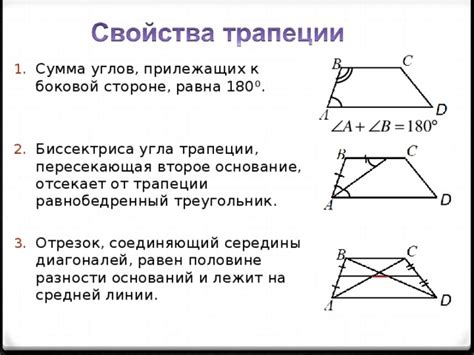
В данном разделе представлены примеры решения разнообразных задач, связанных с определением углов фигуры, которая имеет две параллельные стороны и среднюю линию, которая соединяет середины этих сторон.
В первом примере задачи требуется найти значения углов трапеции, при условии что известны длины её сторон и средней линии. Автор приводит подробное решение задачи, используя математические формулы и логику.
Во втором примере представлен сложный случай, когда известны только значения двух углов трапеции и длина средней линии. Автор демонстрирует, как с помощью логических рассуждений и геометрических преобразований можно найти остальные углы фигуры.
Третий пример основан на реальной ситуации, где известны значения угла и двух сторон трапеции. Автор предлагает использовать принципы тригонометрии и теоремы о треугольниках, чтобы определить остальные углы фигуры.
Четвёртый пример является задачей на нахождение углов трапеции с использованием формулы площади фигуры и длины её сторон. Автор подробно объясняет все шаги решения задачи и предлагает примеры вычислений.
Пятый пример представлен в виде головоломки, которая предлагает найти значения углов трапеции, используя логические рассуждения и анализ геометрических свойств фигуры. Автор предлагает нестандартное и интересное решение задачи.
Упражнения для закрепления полученных знаний

Этот раздел предлагает ряд практических упражнений, которые помогут вам закрепить материал, изученный в предыдущих разделах. Они не только позволят вам лучше понять тему, но и развить навыки решения задач и аналитического мышления.
- Решите следующие задачи, используя изученные методы и формулы:
- Найдите все углы данной фигуры, имеющей две параллельные стороны и две непараллельные стороны.
- Докажите, что сумма всех углов данной фигуры всегда равна 360 градусов.
- Определите площадь трапеции по заданным сторонам и средней линии.
- Создайте несколько трапеций с различными значениями сторон и средней линии. Используйте изученные методы для нахождения углов каждой из фигур, а затем сравните результаты.
- Изучите свойства трапеции с равными основаниями. Какие углы она образует? Каковы соотношения между сторонами и углами в такой фигуре?
- Решите геометрическую задачу, в которой нужно найти все углы трапеции, зная только одну его сторону и диагональ.
- Докажите, что сумма углов в выпуклом многоугольнике всегда равна 180*(n-2) градусов, где n - количество его сторон.
Постепенно увеличивайте сложность задач и использование найденных решений в реальных ситуациях. Это поможет вам лучше понять применение методов нахождения углов трапеции по сторонам и средней линии и повысить свою геометрическую эрудицию.
Практическое применение методики: решение геометрических задач с помощью универсального подхода

Определять углы трапеции по известным данным может показаться сложной задачей. Однако, с использованием разработанной методики, вы сможете легко и быстро решить подобные геометрические задачи.
Приверженность точности и эффективности – основные принципы, лежащие в основе данного подхода. Сочетание использования длин сторон трапеции, ее средней линии и синонимов математических понятий позволяет получить точные результаты, сохраняя простоту и удобство использования методики.
Практическое применение методики не ограничивается лишь решением учебных задач. Ее универсальность позволяет применять ее во многих областях, требующих точных геометрических расчетов. От строительства и архитектуры до дизайна и машиностроения - данный подход является незаменимым инструментом для решения различных задач.
Закрепите свои знания о методике и попробуйте ее применить на практике. Вы удивитесь, насколько эффективно и удобно можно использовать данный подход для решения геометрических задач.
- Обратите внимание на значимость измерения сторон трапеции для точности вычислений.
- Помните, что средняя линия трапеции является средним арифметическим измерений двух параллельных сторон.
- В процессе вычислений используйте геометрические формулы и свойства трапеции для нахождения углов.
- При работе с комплексными трапециями не забывайте о правилах векторной арифметики.
- Проверяйте полученные результаты с помощью аккуратных измерений и геометрических рассуждений.
- Используйте специализированные геометрические программы для автоматического расчета углов трапеции.
В целом, следуя данным рекомендациям, вы сможете более точно и эффективно находить углы трапеции по известным сторонам и средней линии. Это поможет вам в решении различных задач, связанных с анализом и конструированием треугольников различных форм и размеров.
Вопрос-ответ

Как найти углы трапеции по известным сторонам и средней линии?
Для нахождения углов трапеции по сторонам и средней линии можно использовать метод с использованием формулы для тангенса. Первым шагом необходимо найти значения всех сторон трапеции и ее средней линии. Затем вычисляются углы с помощью обратной функции тангенса и полученных значений сторон. Детальный алгоритм нахождения углов доступен в статье.
Какие данные нужны для применения методики нахождения углов трапеции?
Для применения методики нахождения углов трапеции по сторонам и средней линии необходимы значения всех сторон трапеции и ее средней линии. Без этих данных невозможно вычислить углы.
Можно ли использовать эту методику для решения задач на нахождение углов трапеции в школьных уроках?
Да, эту методику можно использовать для решения задач на нахождение углов трапеции в школьных уроках. Она является эффективным инструментом и позволяет с уверенностью решать задачи данного типа.
Какие преимущества есть у методики нахождения углов трапеции по сторонам и средней линии?
Методика нахождения углов трапеции по сторонам и средней линии имеет несколько преимуществ. Во-первых, она позволяет решать задачи данного типа достаточно быстро и точно. Во-вторых, не требует сложных математических выкладок и специальных инструментов. В-третьих, она доступна для использования как в школьных условиях, так и в профессиональной деятельности.
Может ли использование методики нахождения углов трапеции по сторонам и средней линии привести к неточному результату?
Все зависит от правильности определения значений сторон трапеции и ее средней линии. Если эти данные определены точно, то методика будет давать точные результаты. Однако, если данные содержат неточности или углы трапеции близки к 180 градусам, возможны небольшие погрешности в вычислениях.
Какие методики существуют для нахождения углов трапеции?
Для нахождения углов трапеции существует несколько методик. Одна из них основывается на использовании сторон и средней линии трапеции. Другие методики включают использование диагоналей, высоты и прямых углов.



