Изучение геометрии требует не только понимания основных понятий и законов, но и умения применять полученные знания на практике. Одной из важных задач является доказательство того, что два треугольника равны друг другу. В данной статье мы рассмотрим основные методы и способы подтверждения эквивалентности треугольников ABC и CBD.
Вторым методом является применение основных теорем геометрии. Одна из таких теорем - теорема о равенстве треугольников по двум сторонам и углу между ними (ССУ). Согласно этой теореме, если два треугольника имеют две равные стороны и равный им угол между ними, то треугольники равны. Применение этой теоремы может быть полезным при доказательстве эквивалентности треугольников ABC и CBD.
Использование принципа равных углов

Ценность принципа равных углов в доказательстве равенства треугольников неоспорима. Этот принцип сопровождает нас в исследовании геометрии, позволяя установить равенство двух треугольников на основе равенства соответствующих углов.
Принцип равных углов основывается на том, что если в двух треугольниках одинаково направленные углы считаются равными, то сами треугольники считаются равными. Этот метод, комбинируясь с другими геометрическими доказательствами, позволяет строить надежные и строгие доводы при проверке равенства треугольников.
Применение принципа равных углов в доказательстве равенства треугольников требует внимательного анализа соответствующих углов и их расположения в треугольниках. Важно учесть, что использование принципа равных углов следует подтверждать другими методами, такими как равенство сторон или равенство других углов треугольников.
Принцип равных углов является одной из ключевых стратегий в доказательстве равенства треугольников и значительно облегчает процесс решения геометрических задач. Внимательное применение этого принципа позволяет устанавливать равенство треугольников и продвигаться вперед в изучении геометрии, набирая навыки аналитического мышления и логического рассуждения.
Применение правила SSS (сторона-сторона-сторона)
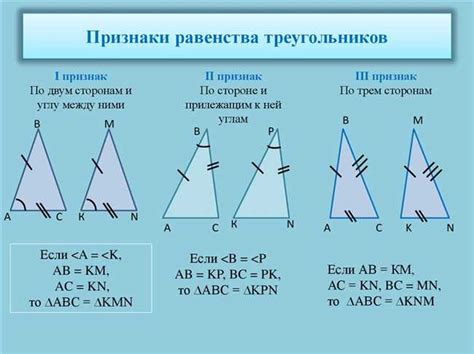
Принцип SAS в доказательстве равенства треугольников

Один из методов, позволяющих доказать равенство двух треугольников, основывается на принципе SAS, что означает равенство сторона-угол-сторона. Этот принцип гласит, что если в двух треугольниках соответственно равны одна сторона, прилежащий к ней угол и другая прилежащая сторона, то треугольники равны.
Принцип SAS является основой для множества доказательств равенства треугольников и может быть использован в различных задачах геометрии. Данный метод позволяет упростить и ускорить процесс доказательства, ибо требует всего лишь равенства трех элементов: стороны, угла и стороны.
Как применить принцип SAS для доказательства равенства треугольников? Сначала необходимо найти равные стороны в двух треугольниках и убедиться, что они примыкают к противоположным равным углам. Затем находится равенство между углами. Наконец, устанавливается равенство между сторонами. Если все три условия выполняются, то треугольники доказано равными по принципу SAS.
Стоит отметить, что применение принципа SAS требует аккуратного и систематического подхода, чтобы убедиться, что все требуемые условия выполнены. Кроме того, при доказательстве равенства треугольников необходимо быть внимательным к примыкающим к равным сторонам углам и углам прилежащим к равным сторонам.
Применение теоремы о равнобедренности треугольников

Эта теорема позволяет нам установить равенство треугольников, не прибегая к сложным методам доказательства. В основе теоремы лежит принцип равенства боковых сторон и углов у равнобедренных треугольников.
Равнобедренные треугольники - это треугольники, у которых две стороны равны между собой и два угла при основании равны.
Применение этой теоремы позволяет нам не только доказывать равенство треугольников, но и решать разнообразные задачи, связанные с равнобедренными треугольниками.
Например, мы можем использовать теорему о равнобедренности треугольников, чтобы найти значения неизвестных сторон и углов в задаче, где нам известны только некоторые параметры треугольника.
Также, мы можем применить данную теорему, чтобы доказать равенство фигур, состоящих из равнобедренных треугольников. Это может быть полезно, когда нам нужно установить равенство двух сложных многоугольников или фигур.
Итак, теорема о равнобедренности треугольников является мощным инструментом, который позволяет нам упростить доказательство равенства треугольников и решение задач, связанных с равнобедренными треугольниками.
Использование понятия равных высот

Равные высоты, или высоты треугольника, представляют собой перпендикулярные отрезки, проведенные из вершин треугольника к противоположным сторонам. Равенство высот означает, что их длины совпадают, что ведет к аналогичным свойствам треугольников, опирающихся на эти высоты.
Использование понятия равных высот позволяет установить равенство треугольников на основе сходства между их сторонами и углами. Этот метод часто используется для доказательства совпадения треугольников, основываясь на равенстве длин отрезков между высотами.
Применение понятия равных высот предоставляет нам дополнительный инструмент для анализа и доказательства равенства треугольников, что упрощает работу с данной геометрической задачей и открывает новые возможности для поиска решений.
Принцип AAS: углы, сторона, углы

Доказательство равенства треугольников по принципу AAS является одним из основных методов, применяемых в геометрии. Данный принцип позволяет установить, что два треугольника равны, если у них равны два угла, одна сторона между этими углами также равна, а совпадающие стороны расположены между равными углами.
Доказательство равенства треугольников по принципу AAS происходит следующим образом: вначале устанавливается равенство двух углов у треугольников, затем доказывается равенство общей стороны, а затем дополнительно устанавливается равенство соответствующих углов. В результате такого доказательства можно с уверенностью утверждать, что треугольники полностью равны.
Принцип AAS является важной базой для решения различных геометрических задач, включая определение равенства треугольников с использованием других методов и принципов. Знание этого принципа позволяет более глубоко понимать структуру и взаимосвязь треугольников, а также успешно применять его в решении задач как в учебе, так и в практической геометрии.
Таким образом, принцип AAS является надежным и эффективным методом доказательства равенства треугольников, основывающимся на сравнении углов и сторон.
Использование принципа HL для доказательства равенства треугольников

В данном разделе рассматривается применение теоремы о равенстве треугольников по принципу HL (сторона-легкость). Этот метод позволяет установить равенство двух треугольников, исходя из равенства одной стороны и угла при этой стороне, а также равенства легкости (перпендикулярности). Это один из основных принципов в геометрии, который обладает широким применением и обеспечивает достаточную информацию для доказательства равенства треугольников.
| Шаги | Описание |
|---|---|
| Шаг 1 | Выберите два треугольника, между которыми требуется доказать равенство. |
| Шаг 2 | Определите сторону-легкость, то есть сторону, которая равна в обоих треугольниках, и угол при этой стороне, который также равен. |
| Шаг 3 | Установите равенство легкостей (перпендикулярности) между соответствующими сторонами треугольников. |
| Шаг 4 |
При использовании принципа HL необходимо быть внимательным и точным в выборе сторон-легкостей. Корректное определение этих элементов позволяет получить надежное доказательство равенства треугольников. Применение этого метода является эффективным способом в геометрии для проверки равенства треугольников и решения связанных задач.
Вопрос-ответ

Как доказать равенство треугольника ABC и треугольника CBD?
Для доказательства равенства треугольников ABC и CBD необходимо найти совпадающие стороны и углы, а также обратить внимание на данные условия задачи. Если все стороны и углы в треугольниках совпадают, то мы можем сделать вывод о их равенстве.
Какие методы и приемы можно использовать для доказательства равенства треугольников?
Для доказательства равенства треугольников можно использовать такие методы и приемы, как совпадение сторон и углов, а также использование теорем и свойств треугольников.
Какие основные свойства треугольников помогут в доказательстве их равенства?
Основные свойства треугольников, которые помогут в доказательстве их равенства, включают равенство соответствующих сторон и углов, равенство сторон и углов с использованием транзитивности, а также равенство треугольников при равенстве двух сторон и угла между ними.
Какие условия должны быть выполнены для доказательства равенства треугольников?
Для доказательства равенства треугольников необходимо, чтобы совпадали все стороны и углы в обоих треугольниках, или же чтобы совпадали две стороны и угол между ними. Также, в некоторых случаях, указанные условия могут быть изменены в соответствии с данными задачи.
Какие теоремы помогут в доказательстве равенства треугольников?
Для доказательства равенства треугольников можно использовать такие теоремы, как теорема о совпадении треугольников по трем сторонам (ССС), теорема о совпадении треугольников по двум углам и вложенной стороне (УУВ), а также теорема о совпадении треугольников по двум сторонам и углу между ними (СУУ).



