Разнообразие методов построения взвешенного графа по таблице позволяет нам исследовать и визуализировать связи между различными элементами. Однако, прежде, чем приступить к рассмотрению алгоритмов и примеров, давайте осознаем общую идею и цель данного раздела.
Основная задача данной статьи заключается в описании подходов к построению уникальных и информативных графов на основе данных, содержащихся в таблице. Благодаря весам, или связям, указанным в таблице, мы можем представить различные отношения и взаимосвязи между элементами, что облегчает наше понимание и анализ датасета.
Взвешенные графы, полученные из таблицы, позволяют нам определить наиболее значимые элементы, выделить основные кластеры и идентифицировать самые сильные связи. Подобные методы имеют широкие применения в различных сферах, начиная от анализа социальных сетей и заканчивая диагностикой сетей передачи данных.
Четыре основных подхода к созданию взвешенного графа на основе данных табличного вида

Для визуализации и анализа связей между различными элементами, представленными в таблице, существует множество методов, позволяющих построить взвешенный граф. В данном разделе рассмотрим четыре основных подхода к созданию графа, основанные на специфическом использовании данных из таблицы и учете влияния их веса на структуру графа.
1. Метод рангов
Один из наиболее распространенных способов построения взвешенного графа - это использование метода рангов. Он позволяет назначить каждому элементу в таблице определенный ранг или вес, который определяет его важность или степень влияния на другие элементы. Таким образом, граф будет отражать взаимосвязи между элементами, учитывая их значимость в контексте исследуемых данных.
2. Метод сходства
Другим методом построения взвешенного графа является метод сходства. С его помощью определяется степень близости или сходства между элементами, представленными в таблице. Чем более похожи элементы, тем больший вес им будет присвоен. Этот метод особенно полезен в анализе данных, где важно выявить группы или кластеры элементов на основе их сходства.
3. Метод вероятности
Метод вероятности основан на расчете вероятности возникновения определенной связи между элементами таблицы. Вес каждой связи определяется как вероятность ее наличия, и этот вес учитывается при построении графа. Такой подход особенно эффективен в анализе больших объемов данных, где возможно проследить множество взаимосвязей.
4. Метод важности
Метод важности основан на определении степени важности каждого элемента таблицы в контексте исследуемых данных. Чем больше важность у элемента, тем больший вес он получит в графе. Этот метод помогает выделить ключевые элементы и центральные узлы в сети связей, что позволяет более детально изучить их влияние на всю структуру графа.
Матрица смежности
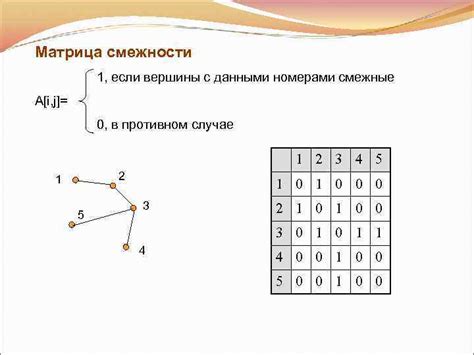
Матрица смежности -- это структура данных, которая помогает описать отношения между вершинами графа. Она представляется в виде квадратной матрицы, где строки и столбцы соответствуют вершинам графа, а элементы матрицы обозначают наличие или отсутствие ребра между соответствующими вершинами.
Матрица смежности широко используется при анализе различных типов графов, таких как направленные и ненаправленные графы, ориентированные и неподвижные графы. Эта структура данных обладает рядом преимуществ, таких как простота хранения и быстрый доступ к информации о смежных вершинах.
Для представления матрицы смежности в программном коде обычно используется двумерный массив. Элементы этого массива могут быть логическими значениями (true/false) для ненаправленных графов или целыми числами для направленных графов, обозначающими вес ребра. Если между вершинами отсутствует ребро, то соответствующий элемент матрицы равен нулю или имеет специальное обозначение "бесконечность".
Преимущества матрицы смежности включают простоту реализации алгоритмов поиска и обхода графов, а также возможность быстро определять наличие ребра между двумя вершинами. Однако она может быть неэффективной для больших и разреженных графов, так как занимает много памяти и требует обновления при добавлении или удалении вершин и ребер.
Список смежности
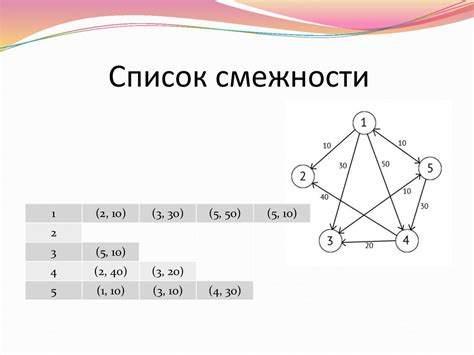
В таблице, представляющей список смежности, каждая строка соответствует отдельной вершине графа. В ячейках данной строки указываются связанные с данной вершиной вершины и их веса. Таким образом, список смежности представляет собой массив списков, где каждый элемент списка содержит номер вершины и вес связи.
| Вершина | Список смежности |
|---|---|
| 1 | [2: 3] [3: 1] [4: 2] |
| 2 | [1: 3] [3: 2] [5: 4] |
| 3 | [1: 1] [2: 2] [4: 2] [5: 3] |
| 4 | [1: 2] [3: 2] [5: 1] |
| 5 | [2: 4] [3: 3] [4: 1] |
Такой способ представления графа позволяет не только легко хранить и визуализировать его структуру, но и эффективно осуществлять различные операции, такие как поиск смежных вершин, вычисление степеней вершин и т.д. Кроме того, список смежности обеспечивает экономию памяти, поскольку хранит только информацию о реально существующих связях между вершинами.
Матрица инцидентности: взаимосвязи элементов в графе
Матрица инцидентности является двумерным массивом, где строки соответствуют вершинам графа, а столбцы - ребрам. Каждая ячейка матрицы содержит число, которое указывает на тип связи между определенной вершиной и ребром. Если связь отсутствует, ячейка содержит 0, если вершина и ребро связаны, то значение ячейки - 1.
Взглянув на матрицу инцидентности, мы можем однозначно определить, какие вершины имеют связь с данным ребром, а также вычислить количество связей, участвующих в графе.
Преимущество использования матрицы инцидентности заключается в ее простоте и удобстве представления сложных графов. Кроме того, матрица инцидентности также может иметь дополнительную информацию о весе ребра, что позволяет рассматривать графы с разными уровнями взаимосвязей между элементами.
Разнообразные способы создания информативного графического отображения данных
В данном разделе будут рассмотрены различные подходы и методы, позволяющие создать наглядное и понятное графическое отображение информации на основе имеющейся таблицы с данными.
- Интерактивные графики: позволяют представить данные в виде динамических графиков, где пользователь может взаимодействовать с информацией, выбирать конкретные параметры и получать дополнительные детали. Это может быть полезным при анализе больших объемов данных или при необходимости сравнить различные показатели.
- Использование цветовой гаммы: правильное использование цветов может помочь выделить ключевые моменты, сделать информацию более понятной и запоминающейся. Можно использовать разные оттенки одного цвета для обозначения разных категорий или используя контрастные цвета, создать яркое и привлекательное визуальное отображение данных.
- Диаграммы и графики: это визуальные средства представления данных в виде точек, линий, колонок и других графических элементов. Разные типы графиков, такие как столбчатые диаграммы, круговые диаграммы, диаграммы рассеивания и т.д., могут быть использованы для построения различных типов данных.
- Использование иконок и символов: можно добавить значимость и легкость восприятия данных, используя иконки и символы, которые ассоциируются с конкретными понятиями или предметами. Например, для обозначения температуры можно использовать иконку термометра, а для обозначения времени - иконку часов.
Таким образом, выбор определенного метода или их комбинирование зависит от целей визуализации данных и особенностей таблицы, представляющей информацию. Целью является создание наглядного и понятного графического отображения данных, которое поможет пользователям увидеть связи, тенденции и особенности внутри представленной информации.
Вопрос-ответ

Как можно построить взвешенный граф по таблице?
Для построения взвешенного графа по таблице существует несколько методов. Один из них - это метод смежностей, при котором каждой вершине графа соответствует строка таблицы, а каждому ребру - столбец таблицы. Вес ребра равен значению ячейки. Другой метод - это метод инцидентностей, при котором каждой вершине графа соответствует столбец таблицы, а каждому ребру - строка таблицы. Вес ребра также равен значению ячейки.
Какие еще методы используются для построения взвешенного графа по таблице?
Помимо методов смежностей и инцидентностей, существует еще метод преобразования таблицы в матрицу смежности. При этом каждый элемент матрицы будет соответствовать ребру графа, а его значение - весу этого ребра. Также можно использовать метод списка ребер, при котором в таблице перечисляются все ребра графа с их весами.



