В современном мире, где скорость и точность расчетов играют решающую роль, правильное выбор числовых параметров становится жизненно важным. Однако, требования и ограничения к эффективности расчетов очень разнообразны, а идеальное соотношение чисел может быть весьма субъективным понятием.
Ключевым моментом в достижении оптимального соотношения чисел является применение комплексного подхода, учитывающего различные параметры и их взаимосвязи. Ведь каждое число в расчете имеет свою функцию и значение, и их гармоничное сопоставление важно для точности результатов.
Как определить оптимальное соотношение чисел? Один из подходов вытекает из принципа "есть много способов достичь одной цели". Это означает, что выбор числовых параметров может зависеть от конкретной задачи и контекста в котором она решается. Необходимый баланс может быть достигнут только после тщательного анализа и экспериментов с разными сочетаниями чисел.
Основные принципы соотношения чисел в математических расчетах
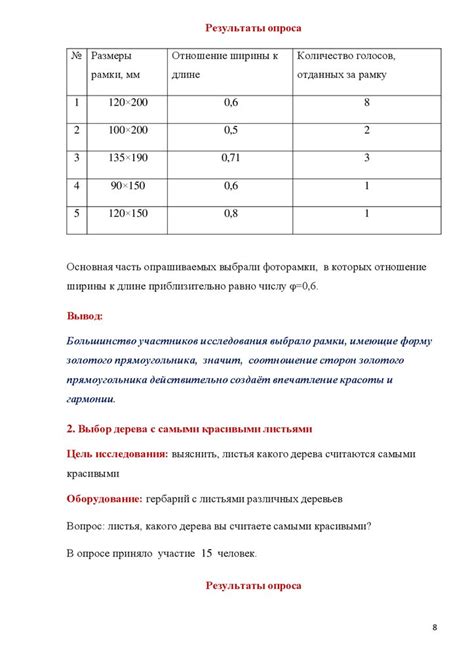
В математических расчетах существуют основные принципы, которые определяют соотношение чисел и отношение между ними. Эти принципы позволяют эффективно выполнять расчеты и получать точные результаты.
Один из важных принципов – принцип пропорциональности. Он заключается в том, что если две величины имеют пропорцию, то их соотношение остается постоянным. Это позволяет использовать пропорции в расчетах для нахождения неизвестных значений.
Другой принцип – принцип равенства. Он используется, когда две или более величины равны между собой. По этому принципу можно выполнять математические операции, сравнивать значения и получать точные результаты.
Важным элементом математических расчетов является также принцип противоположности. Он гласит, что для каждого положительного числа существует противоположное ему отрицательное число, и наоборот. Это позволяет выполнять операции с отрицательными числами и учитывать их в расчетах.
| Принцип | Описание |
|---|---|
| Принцип пропорциональности | Соотношение чисел остается постоянным |
| Принцип равенства | Две или более величины равны между собой |
| Принцип противоположности | Присутствие положительных и отрицательных чисел |
Учитывайте особенности задачи и цели расчетов

Когда речь идет о выполнении эффективных расчетов, важно учитывать природу задачи и цели, которые мы ставим перед собой.
Каждая задача требует своего подхода к выбору чисел и их соотношения, чтобы достичь наилучших результатов. От выбора правильных чисел будет зависеть точность и скорость расчетов, а также возможность получить полное понимание процессов, которые мы анализируем.
При решении математических задач, например, нам может потребоваться учитывать такие величины, как коэффициенты, параметры и показатели. Их соотношение должно быть подобрано таким образом, чтобы исключить возможные ошибки и недостаточность информации.
В других случаях, например, при финансовых расчетах, необходимо учитывать факторы, такие как процентные ставки, инфляция, доходы и расходы. Устанавливая правильное соотношение между этими числами, мы можем прогнозировать будущие результаты, а также принимать обоснованные решения.
Применение математических моделей и методов также является неотъемлемой частью многих задач и расчетов. При выборе чисел и их соотношения мы должны учитывать особенности и ограничения этих моделей, чтобы извлечь максимальную пользу и достичь точных результатов.
- При работе с большими объемами данных и анализом их статистических показателей, важно учитывать выборку, дисперсию и средние значения.
- При проектировании и строительстве, мы должны учитывать соотношение между параметрами материалов, нагрузками и безопасностью конструкции.
- Аналитические расчеты могут требовать учета различных физических законов и свойств, чтобы найти оптимальное решение.
Итак, каждая задача и каждая цель требуют особого подхода к выбору чисел и их соотношений. Учитывайте природу задачи, а также следуйте принципам достижения точности и эффективности, чтобы получить наилучшие результаты при расчетах.
Сбалансируйте точность и скорость вычислений для оптимальных результатов

При проведении расчетов очень важно найти оптимальное соотношение между точностью и скоростью вычислений. Важно учесть, что увеличение точности может привести к увеличению времени выполнения, а повышение скорости может привести к потере некоторой точности.
Оптимальное соотношение позволяет достичь эффективности в вычислениях, где результаты будут достаточно точными, но время выполнения будет минимальным. Для этого необходимо анализировать требования задачи и на основе этого выбирать подходящий метод и алгоритм расчета.
Один из способов сбалансировать точность и скорость - это использование приближенных методов расчета. Приближенные методы позволяют получить результаты с определенной степенью точности, однако требуют меньше времени на вычисление. Важно выбрать метод, который обеспечивает достаточно точный результат для конкретной задачи, чтобы избежать возможных ошибок в дальнейших расчетах.
Еще один способ достижения баланса между точностью и скоростью - это использование параллельных вычислений. Параллельные вычисления позволяют распараллелить выполнение задачи на несколько независимых частей, что позволяет сократить время выполнения. Однако для достижения оптимальных результатов необходимо правильно разбить задачу на подзадачи, выбрать верное количество параллельных потоков и эффективно использовать ресурсы вычислительной системы.
Важно также учитывать, что не всегда необходимо стремиться к максимальной точности или максимальной скорости. В некоторых случаях достаточно достичь приемлемого уровня точности и выполнить расчеты в разумное время. Для этого следует анализировать требования задачи и руководствоваться их особенностями.
Итак, соблюдение баланса между точностью и скоростью вычислений является ключевым фактором для достижения оптимальных результатов. При выборе методов и алгоритмов необходимо учитывать требования задачи и выбирать оптимальное соотношение между точностью и скоростью, чтобы достичь высокой эффективности расчетов.
Используйте статистические данные и предыдущий опыт
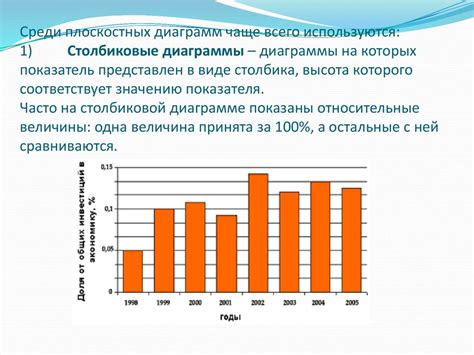
Статистические данные позволяют нам обнаруживать тенденции и закономерности в процессе расчетов. Они позволяют нам понять, как различные числа взаимосвязаны и как они влияют на результат. Использование этих данных помогает нам прогнозировать будущие значения и принимать решения на основе объективных фактов.
Также важно учитывать предыдущий опыт при построении правильного соотношения чисел для расчетов. Анализировать прошлые случаи позволяет нам извлечь уроки и избежать повторения ошибок. Опытные специалисты могут предложить эффективные стратегии и методики, которые позволят достичь точных и быстрых результатов.
Конечно, каждый расчетный процесс уникален, и требуется гибкий подход к выбору соотношения чисел. Но использование статистических данных и предыдущего опыта является надежной основой для построения правильного соотношения чисел и достижения эффективных результатов в расчетах.
Вопрос-ответ

Какие числа нужно использовать для эффективных расчетов?
Для эффективных расчетов следует использовать такие числа, которые обеспечивают достаточную точность при минимальных затратах на вычисления. Это могут быть как целые числа, так и числа с плавающей точкой, в зависимости от конкретной задачи и требуемой точности расчетов.
Как правильно выбрать соотношение чисел для эффективных расчетов?
Правильный выбор соотношения чисел для эффективных расчетов зависит от нескольких факторов. Прежде всего, необходимо определить требуемую точность расчетов и выбрать числовые типы данных, которые обеспечат необходимую точность. Также важно учитывать ограничения на вычислительные ресурсы, такие как доступная память и производительность процессора. В некоторых случаях может понадобиться использовать различные числовые форматы для разных этапов расчетов, чтобы обеспечить оптимальное соотношение скорости и точности.



