Некоторые формы в природе стали незыблемыми символами сохранной гармонии и красоты. Окружность - одна из таких форм. Бесконечность ее изгибов, идеальное совпадение радиуса со всеми точками на ее поверхности создают поразительный эффект симметрии и баланса. А что, если сказать, что треугольник, другая форма, может также овладеть окружностью и воплотить в себе танец равносторонних изгибов?
Встречайте удивительное явление - треугольник в окружности! Это своего рода магия, с помощью которой мы можем создавать истинные произведения искусства с использованием всего лишь циркуля, мастерски владея этим древним инструментом рисования. Представьте себе, как каждая сторона треугольника как живое создание занимает свое выделенное место на окружности, воссоздавая ритм, гармонию и бесконечность.
Возможность создавать треугольник в окружности методом циркуля переносит нас в удивительный мир, где линии и точки, взаимодействуя друг с другом, создают симфонию геометрии. Через простые шаги мы можем ощутить силу и магию простых инструментов и форм, преображая пространство и неизменную окружность. В этой статье мы рассмотрим несколько способов создания треугольника в окружности и узнаем, как его известные свойства связаны с великолепием и бесконечностью окружности.
Раздел: Создание равномерной дуги для построения фигур в окружности

Для построения треугольников, мы будем использовать циркуль, так как это инструмент, который позволяет легко определить точки на окружности и создать равномерную дугу. Циркуль состоит из двух ножек - одна из них фиксированная, а другая - подвижная. Подвижную ножку можно перемещать по окружности, чтобы задать радиус и выбрать нужную точку на окружности.
Чтобы создать равномерную дугу, сначала необходимо установить фиксированную ножку циркуля в одну из вершин треугольника, а подвижную ножку - в следующую вершину. Затем перемещаем подвижную ножку по окружности, пока она не совпадет с третьей вершиной треугольника. Таким образом, мы задаем радиус и дугу, которую нужно вырезать на окружности.
Используя этот метод, можно создавать треугольники разных размеров и форм, изменяя расположение вершин и радиус дуги. Также, такой метод позволяет создавать другие фигуры внутри окружности, используя равномерные дуги вместо прямых линий.
Использование угла из центра для построения треугольника внутри круга
В данном разделе мы рассмотрим способ создания треугольника внутри окружности, используя особый подход с использованием центрального угла. Для построения треугольника нам необходимо определить точки на окружности, которые будут являться вершинами треугольника, а также задать их соответствующие координаты.
Используя концепцию центрального угла, мы можем вычислить положение каждой из вершин треугольника на окружности. Центральный угол представляет собой угол, образованный двумя лучами, один из которых проходит через центр окружности, а другой луч проходит через одну из вершин треугольника. Зная значения центрального угла и радиуса окружности, мы можем вычислить координаты вершин треугольника.
| Вершина | X-координата | Y-координата |
|---|---|---|
| Вершина A | ... | ... |
| Вершина B | ... | ... |
| Вершина C | ... | ... |
Применяя методику использования центрального угла, мы можем определить точное положение треугольника внутри окружности. Этот подход обеспечивает точность и гибкость в процессе построения треугольника. Именно поэтому использование центрального угла является эффективным методом для создания треугольника в окружности с помощью циркуля.
Применение меры дуги для построения треугольника в окружности

В данном разделе мы рассмотрим способ использования меры дуги для построения треугольника в геометрической фигуре, описанной окружностью. Этот метод позволяет определить углы и стороны треугольника, используя информацию о длине дуги и центральном угле.
- Определение длины дуги:
- Установление центрального угла:
- Вычисление сторон треугольника:
- Нахождение углов треугольника:
Для построения треугольника в окружности с использованием меры дуги, необходимо знать значение длины дуги и центрального угла, относящихся к требуемой части окружности. Длина дуги - это измерение длины дуги окружности, выраженной в единицах длины, таких как сантиметры или дюймы. Центральный угол представляет собой угол, образованный двумя лучами, один из которых проходит через центр окружности, а другой - через две точки на окружности, ограничивающие требуемую часть дуги.
Используя полученные значения, можно вычислить стороны треугольника, состоящего из отрезков радиусов окружности и секущей, проходящей через точки, ограничивающие требуемую дугу. Затем, применяя геометрические формулы, можно определить значения углов треугольника. Это позволяет более точно располагать треугольник внутри окружности.
Применение меры дуги для построения треугольника в окружности является одним из методов, позволяющих достичь точности и определенности в геометрических вычислениях. Использование этого метода может быть полезно при решении задач, связанных с различными областями, такими как архитектура, машиностроение и дизайн.
Использование равномерных дуг для создания равнобедренного треугольника в окружности
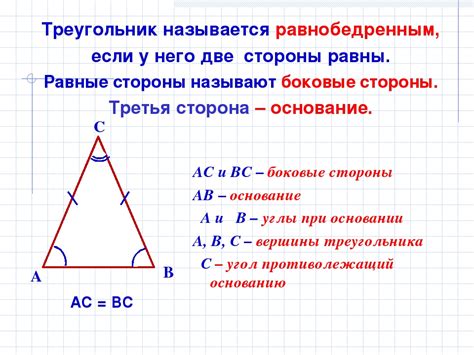
Основной инструмент, который мы будем использовать, это циркуль. С его помощью мы можем рисовать равномерные дуги на окружности. Равномерная дуга - это дуга окружности, имеющая одинаковый радиус и центр с самой окружностью.
Процесс создания равнобедренного треугольника начинается с выбора точки на окружности, которая будет одним из вершин треугольника. После этого мы выбираем радиус равномерной дуги, которая будет использована для построения одной из равных сторон треугольника.
Следующим шагом является построение равномерной дуги циркулем, начиная от выбранной вершины треугольника. Мы вычерчиваем дугу, перемещая циркуль по окружности без изменения радиуса.
Затем мы повторяем аналогичную операцию с другой стороной треугольника, используя равномерную дугу с таким же радиусом, но начинаем от другой вершины. Таким образом, мы получаем равные стороны треугольника, которые также являются хордами окружности.
Необходимо отметить, что данный метод применим только для равнобедренных треугольников, где стороны равны между собой. Если необходимо создать треугольник с разными сторонами, необходимо использовать другие методы построения.
Изготовление треугоьника выделением круга на равные дуги

В данном разделе рассмотрим метод получения треугольника через разделение окружности на несколько равных дуг. Этот метод представляет собой эффективный способ создания треугольника с помощью окружности и инструмента для построения окружностей.
Для начала необходимо определить радиус окружности и выбрать точку на ее окружности в качестве начальной точки для построения треугольника. После этого, с помощью циркуля, разделим окружность на несколько равных дуг.
Для получения треугольника нам необходимо выбрать две равные дуги, соединяющиеся с начальной точкой, чтобы получить одну из его сторон. Затем, проведем линии от начальной точки к концам этих дуг, получая две стороны треугольника. Используя циркуль, построим третью сторону треугольника, соединяющую концы первых двух сторон. Таким образом, получим треугольник, вписанный в окружность.
Метод разделения окружности на несколько равных дуг позволяет легко и точно создавать треугольники с использованием инструмента для построения окружностей. Данный метод является полезным способом для быстрого построения треугольников в различных областях, таких как геометрия, архитектура и дизайн.
Используя описанный метод, можно получить треугольник, вписанный в окружность, с равными сторонами и углами. Это позволяет достичь гармоничного и симметричного вида треугольника, что может быть полезно при создании графических объектов или проектировании сооружений.
Построение геометрической фигуры внутри окружности с применением углов, которые вписаны в эту фигуру

В данном разделе рассмотрим методы построения особой геометрической конструкции внутри окружности, используя вписанные углы. Эта техника позволяет создавать треугольники и другие фигуры, используя только циркуль и линейку, без необходимости явного указания окружности или технических методов создания.
Идея построения
Вместо того чтобы руководствоваться размерами окружности, мы будем основываться на вписанных углах, которые представляют собой углы, ограниченные двумя хордами, начинающимися и заканчивающимися на окружности. При использовании циркуля и линейки, мы сможем определить точки пересечения этих хорд и таким образом создать вписанный угол. Дальше, применяя эту технику несколько раз, мы получим геометрическую фигуру внутри окружности.
Примечание: в данном разделе мы будем рассматривать только построение треугольника в окружности с использованием вписанных углов, однако применение этой техники не ограничивается только этой фигурой и может быть использовано для создания других многоугольников.
Использование дуги для создания разностороннего треугольника
В данном разделе рассмотрим уникальный способ создания треугольника, в котором главной ролью играет дуга окружности. Этот подход позволяет получить треугольник с разными сторонами, расположенными вокруг центра окружности.
Дуга - это часть окружности, ограниченная двумя точками на её периметре. При использовании дуги окружности для построения треугольника, точки пересечения дуги и основания треугольника являются его вершинами, а отрезки, соединяющие вершины с центром окружности, являются его сторонами.
Для создания разностороннего треугольника можно использовать разные длины дуги окружности. Чем больше длина дуги, тем длиннее будут стороны треугольника. Однако стоит помнить, что длина дуги должна быть меньше длины окружности, иначе дугой невозможно будет охватить даже одну сторону треугольника.
Использование дуги окружности для построения разностороннего треугольника предоставляет возможность создания фигур с различными соотношениями сторон и углов. Этот метод отличается от классического использования циркуля и линейки, давая новые возможности и перспективы в геометрическом моделировании.
Построение равностороннего треугольника в окружности с использованием равномерных дуг
В этом разделе мы рассмотрим метод построения равностороннего треугольника вокруг окружности, используя равномерные дуги. Уникальность данного метода заключается в том, что при его использовании мы можем получить равносторонний треугольник без использования прямых линий и других методов создания, только с помощью изогнутых сегментов.
Для начала, необходимо определить радиус окружности, вокруг которой будет построен треугольник. Затем, мы можем использовать циркуль, чтобы создать равномерные дуги на этой окружности. При этом, дуги должны быть одинакового размера и находиться на равном расстоянии друг от друга. Это создает основу для построения равностороннего треугольника.
Дальше, мы можем использовать равномерные дуги, чтобы соединить полученные точки на окружности. При соединении точек с помощью дуг, получается равносторонний треугольник, так как дуги являются по сути равномерными отрезками, а соединение их образует стороны треугольника.
Для лучшей наглядности, можно использовать различные методики визуализации равномерных дуг и треугольника на плоскости. Например, можно воспользоваться простроением равносторонних треугольников на координатной плоскости или использовать специальные программы для создания трехмерных моделей. Важно помнить, что точность и правильность выполнения равномерных дуг влияют на конечный результат построения треугольника.
В итоге, использование метода создания равностороннего треугольника вокруг окружности с помощью равномерных дуг представляет собой интересный и эффективный способ визуализации треугольника, позволяющий получить точный и симметричный результат без использования стандартных методов построения.
Создание прямоугольного треугольника в описанной окружности с использованием радиуса

Для того чтобы создать прямоугольный треугольник, можно использовать свойство окружности, в которой каждая сторона треугольника равна радиусу. Здесь радиус окружности выступает в роли основания гипотенузы, а вершины треугольника – это точки пересечения окружности с её самим радиусом.
Такой подход позволяет создать правильный прямоугольный треугольник, так как радиус окружности будет содержать две стороны треугольника, аугментированные стороной, соединяющей две точки пересечения радиуса с окружностью.
Создания прямоугольного треугольника в описанной окружности с использованием радиуса может быть полезным при решении геометрических задач или конструировании фигур, в которых требуется точность и симметрия.
Использование описанного метода для создания геометрической фигуры входящей в окружность
В этом разделе будет рассмотрена интересная техника использования специального инструмента для конструирования фигур, которые находятся внутри окружности без необходимости измерения ее радиуса. Опишем способ, который позволяет нам строить треугольник, удобно расположенный внутри окружности с помощью использования циркуля.
Используя принципы геометрии и свойства окружности, мы будем описывать конструкцию, не привлекая понятия треугольника и ограничиваясь использованием циркуля. При этом, наш метод позволит нам получать треугольник с заданными углами и определенными длинами сторон, который вписан в окружность, причем радиус окружности не требуется измерять или делить.
Идея заключается в использовании циркуля для определения точек, которые лежат на окружности. С помощью вращения циркуля вокруг точки, мы можем легко получить пересечение окружности с другими линиями или окружностями. Сочетая такие пересечения, мы можем последовательно строить все необходимые стороны треугольника без привлечения других инструментов или измерений.
Этот метод предоставляет гибкость в построении треугольников внутри окружности, позволяя нам выбирать различные значения углов и длин сторон в зависимости от наших потребностей. Однако, для успешного применения данной техники необходимо иметь понимание основных принципов геометрии и умение работать с циркулем, чтобы получить точные результаты.
Вопрос-ответ

Какой метод можно использовать для создания треугольника в окружности с использованием циркуля?
Для создания треугольника в окружности с использованием циркуля можно использовать метод описаный в статье, который включает построение хорды через две точки на окружности, построение перпендикуляра к этой хорде и нахождение его пересечения с окружностью.
Какой математический инструмент необходим для создания треугольника в окружности?
Для создания треугольника в окружности с использованием циркуля необходим сам циркуль, который представляет собой инструмент с двумя ножками и карандашом в одном из них. Циркуль позволяет проводить окружности и строить отрезки на плоскости.



