Существует огромное множество способов определить центр тяжести треугольника, а одним из наиболее точных и удобных инструментов для этого является циркуль. Позволяющий найти центр тяжести треугольника без особых технических навыков или специализированных математических знаний, циркуль помогает точно определить точку пересечения медиан треугольника, которая является его центром тяжести.
Анализ медиан треугольника является одним из ключевых элементов, на котором основывается методика использования циркуля для поиска центра тяжести треугольника. Медианы треугольника - это линии, соединяющие вершины с противоположными серединами сторон. Используя циркуль, можно найти эти середины и провести медианы треугольника.
С помощью циркуля можно легко найти пересечение медиан треугольника, а именно точку, которая и является его центром тяжести. Комбинация силы гравитации и геометрической точности инструмента обеспечивает высочайшую точность и надежность в определении центра тяжести треугольника с использованием циркуля.
Значение геометрической фигуры и методы определения ее средней точки
Сущность графического изображения, составленного из трех линий, исследуется с точки зрения физической взаимосвязи между элементами. Необходимость определить общий центр "массы" треугольника требует использования геометрических методов в сочетании с знаниями физики, при этом предполагается избегать использования специальных инструментов. Данная статья рассматривает методы определения центра "тяжести" треугольника с использованием простого инструмента.
- Точка пересечения биссектрис
- Медианы треугольника
- Параллельность боковых сторон
В данном разделе будут изложены различные методы нахождения центра "массы" треугольника. Один из них основан на определении точки пересечения биссектрис треугольника, учитывая принцип равенства отношений расстояний от этой точки до соответствующих вершин треугольника. Вторым методом является использование медиан треугольника, определяющих положение его центра "тяжести" с учетом соотношений длин отрезков медиан. Третий метод фокусируется на связи между боковыми сторонами треугольника, исходя из факта параллельности этих сторон через точку, являющуюся центром тяжести.
Практическое применение методов, описанных в данном разделе, позволяет определить центр "массы" треугольника без использования специализированных инструментов, только с помощью простого инструмента - циркуля. В зависимости от контекста и требований, каждый из методов может найти свое применение и помочь в решении конкретной геометрической задачи.
Эволюция использования классического инструмента в создании оси треугольной равновесия

История применения специализированного инструмента для определения центра баланса фигур может быть прослежена далеко в прошлое. Начиная с создания первых ранних версий аналогов, мастера искусства и науки постоянно совершенствовали этот инструмент, который, благодаря его точности и удобству, стал неотъемлемым элементом в построении оси геометрической равновесности. В данном разделе мы рассмотрим важные этапы развития этого инструмента, включая разнообразие техник и методов, которые позволили достичь высокого уровня точности и удобства.
- Происхождение концепции
- Ранние прототипы и инновации
- Революционные методы древних цивилизаций
- Период переосмысления в эпоху Возрождения
- Усовершенствование и улучшение процесса
- Современные техники и области применения
Этот раздел статьи позволит рассмотреть не только эволюцию использования циркуля в построении центра масс треугольника, но и предоставит читателям возможность глубже проникнуть в историческую значимость и техническое достижение, которое влияет на множество научных и технических областей уже многие столетия.
Основные принципы достижения равновесия фигуры с использованием перемещения точек
Этот раздел посвящен основным принципам идеального распределения массы внутри треугольника без использования специальных инструментов или измерительных приборов. В данной технике мы будем сосредоточиваться на перемещении точек и обеспечении их оптимального положения для достижения центра масс в равновесии.
Использование геометрических конструкций. Одним из принципов построения равновесного треугольника является применение геометрических конструкций, таких как биссектрисы и медианы. Биссектрисы делят углы треугольника пополам, а медианы соединяют вершины треугольника с серединами противолежащих сторон. Эти линии позволяют нам определить точки пересечения их продолжений, которые являются потенциальными местами расположения центра масс.
Аккуратность и точность измерений. Важным принципом построения равновесного треугольника является аккуратность и точность измерений. Чтобы достичь равновесия, необходимо аккуратно определить точки пересечения геометрических конструкций и точки массы. Точное измерение позволяет нам определить оптимальное положение точек и обеспечить баланс внутри треугольника.
Экспериментирование с перемещением точек. Один из ключевых принципов построения равновесного треугольника - это экспериментирование с перемещением точек. Путем изменения положения точек, мы можем получить различные комбинации сил и распределений массы внутри треугольника. Экспериментируя с перемещением точек, мы можем найти оптимальное положение, которое обеспечит равновесие и стабильность фигуры.
Понимание принципа равенства моментов. Еще одним важным принципом построения равновесного треугольника является понимание принципа равенства моментов. Момент - это произведение силы и расстояния до определенной точки. Для достижения равновесия, моменты сил, действующих на треугольник, должны быть равны. Чтобы использовать этот принцип, необходимо понять, как расположение точек влияет на распределение массы и моменты сил внутри треугольника.
Итеративный процесс достижения равновесия. Построение равновесного треугольника - это итеративный процесс, который требует последовательных шагов и проверки баланса внутри фигуры. Применение описанных выше принципов и постепенное перемещение точек позволяет нам добиться оптимального распределения массы и достижения равновесия в конечном результате.
Процесс формирования точки равновесия треугольника с применением геометрического инструмента
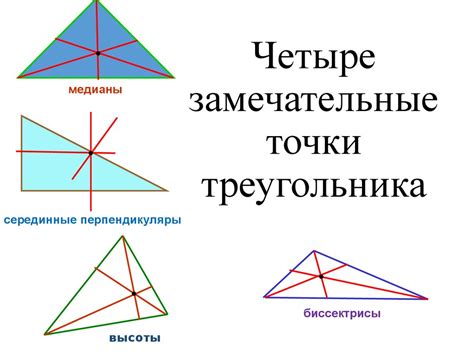
Этот раздел статьи подробно описывает последовательность шагов, необходимых для определения точки, где располагается центр тяжести треугольника. Будут представлены инструкции по использованию специального инструмента, который сумеет помочь определить эту точку, используя только окружности и их центры.
Перед началом построения треугольника необходимо запастись циркулем, при помощи которого можно будет делать различные окружности, а также установить их центры на листе бумаги. Используя эти геометрические инструменты, можно достичь точечного равновесия треугольника без использования каких-либо других математических вычислений.
Первым шагом является выбор трёх точек на листе бумаги, которые будут являться вершинами треугольника. Затем, используя циркуль, необходимо провести поочерёдно окружности, центры которых лежат на серединах соответствующих сторон треугольника. Пересечение этих окружностей будет точкой, где находится центр тяжести треугольника.
Данный метод позволяет с высокой точностью определить расположение центра тяжести треугольника, применяя только геометрические инструменты. С его помощью можно провести построение точки равновесия треугольника достаточно быстро и без использования сложных математических вычислений.
Примеры построения центра масс треугольника с применением переноса точки с помощью двух окружностей
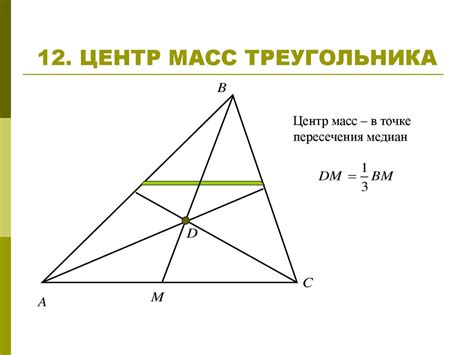
| Пример 1 | Пример 2 |
 |  |
| Описание примера 1 | Описание примера 2 |
В первом примере рассмотрим треугольник ABC с вершинами A, B и C. Все три точки даны на плоскости. Чтобы построить центр масс треугольника, необходимо определить точку D на отрезке AB так, чтобы отношение расстояния от D до A к расстоянию от D до B было равно отношению массы предмета в точке A к массе предмета в точке B. Эта точка D будет центром масс треугольника ABC.
Во втором примере рассмотрим треугольник XYZ с вершинами X, Y и Z. На этот раз все три точки даны на окружности. Чтобы построить центр масс треугольника, необходимо определить точку M на отрезке XY так, чтобы отношение расстояния от M до X к расстоянию от M до Y было равно отношению площади сектора XMY к площади сектора ZMY. Эта точка M будет центром масс треугольника XYZ.
Приведенные примеры демонстрируют применение метода переноса точки с помощью двух окружностей для нахождения центра масс треугольника. Это важная геометрическая задача, которая имеет множество практических применений в различных областях, от архитектуры до физики.
Определение сущности и детали процесса создания гравитационного центра треугольника через инструмент цировки

Процесс конструирования геометрического объекта, который отражает структурную симметрию и баланс составляющих его элементов, представляет собой важный аспект в математике и геометрии. Рассмотрение случая создания центральной точки масс треугольника с использованием инструмента цировки позволяет увидеть специфические аспекты этого процесса.
Обращаясь к инструменту, известному как циркуль, мы можем получить стабильный метод создания центра тяжести треугольника. В ходе конструирования гравитационного центра треугольника с помощью данного инструмента требуется не только знание его основных возможностей, но и понимание их применения в данной задаче.
Практическое применение геометрических центров треугольника и их взаимосвязь с инструментом, упрощающим их построение

В этом разделе мы рассмотрим практическое применение геометрических центров треугольника и их связь с инструментом, который значительно упрощает их построение. Процесс работы с этим инструментом требует использования циркуля, однако существуют различные подходы, при которых его применение может быть облегчено или оптимизировано.
При изучении геометрии, одной из основных задач является определение точек, связанных с треугольником, таких как его центр масс, центр описанной окружности или центр вписанной окружности. Понимание значения и практического применения этих центров позволяет решать различные задачи из областей физики, инженерии, архитектуры и дизайна.
Геометрический центр треугольника, также известный как центр масс или барицентр, является точкой, в которой сосредоточена вся масса треугольника. Это практически значимое понятие, потому что оно позволяет более точно моделировать движение или равновесие системы треугольников, таких как механические конструкции или грузы на кранах.
Геометрический центр треугольника также может быть вычислен с использованием циркуля и синтеза конической инверсии, что позволяет строить его с высокой точностью и предсказуемостью.
Центр описанной окружности треугольника является центром окружности, проходящей через все три вершины треугольника. Этот центр имеет свои практические применения в сферах навигации, обработки изображений, а также в определении географических координат по трем точкам.
Для построения центра описанной окружности треугольника с помощью циркуля, следует использовать срединные перпендикуляры к сторонам треугольника и точки их пересечения.
Центр вписанной окружности треугольника является центром окружности, которая касается всех трех сторон треугольника. Этот центр также имеет практические применения в геометрии, физике и технике, например, при расчете моментов инерции, определении геометрического центра системы точек или при разработке эффективных алгоритмов решения определенных задач.
Основываясь на свойствах центра вписанной окружности, его положение можно определить с помощью циркуля и построения перпендикуляров из вершин треугольника к соответствующим сторонам.
Разнообразные виды ошибок в процессе построения центра тяжести треугольника и способы их избежания
В данном разделе будут рассмотрены разнообразные виды ошибок, которые могут возникнуть при конструировании центра тяжести треугольника, а также представлены методы их предотвращения.
1. Ошибка в определении точек треугольника: одной из основных ошибок является неправильное обозначение вершин треугольника. Ошибочное выбор места треугольника может привести к искажению результатов и получению неверного центра тяжести. Чтобы избежать данной ошибки, необходимо тщательно обозначить вершины, используя ярлыки или обозначения, которые не оставляют места для разночтений.
2. Неправильная конструкция окружностей: при использовании циркуля для построения центра тяжести треугольника возможно допустить ошибки в построении окружностей. Неверные радиусы или несоответствие между окружностями могут привести к неправильному определению центра тяжести треугольника. Для избежания данной ошибки необходимо тщательно отмерить радиусы окружностей и проверить их взаимное расположение.
3. Неправильное определение линий пересечения: при построении центра тяжести треугольника с использованием циркуля, возможно допустить ошибку в определении точек пересечения линий. Неверное определение этих точек приведет к получению некорректного центра тяжести. Чтобы избежать этой ошибки, необходимо внимательно провести линии и проверить точки пересечения, используя дополнительные инструменты или графические методы.
- Использование правильных обозначений вершин треугольника: A, B, C или других ясных обозначений
- Тщательно отмерьте радиусы окружностей и проверьте их взаимное расположение
- Проведите линии внимательно и проверьте точки пересечения
Разнообразие вариантов модификации при создании центров масс треугольника с применением средств из области циркульной геометрии

В данном разделе представлено множество альтернативных подходов к формированию центров тяжести треугольников, используя инструментарий циркуля и линейки. При исследовании различных методов можно наблюдать вариативность в полученных результатах и влияние разных параметров на окончательный результат.
- Модификация с использованием дополнительных медиан.
- Модификация с применением точки Памфилия.
- Модификация с применением компасных преобразований.
- Модификация с использованием дополнительных окружностей.
Вариант модификации предполагает использование дополнительных медиан треугольника для определения центра тяжести. Путем скручивания и пересечения медиан можно определить точку, которая будет играть роль центра масс треугольника.
Некоторые исследователи предлагают использовать точку, названную в честь античного математика Памфилия, для построения центра тяжести треугольника. Данный метод основан на использовании эксцентрических окружностей и касательной, проведенной к одной из них.
Компасные преобразования могут быть использованы для модификации процесса построения центра тяжести треугольника. Применение различных комбинаций движений и поворотов позволяет получить разные результаты, которые отражают особенности данного подхода.
Дополнительные окружности могут быть включены в процесс построения центра тяжести треугольника. Путем проведения дополнительных линий и касаний к окружностям можно определить нужную точку, играющую роль центра масс.
Выбор конкретного метода модификации зависит от задач и требуемых результатов. Использование различных подходов и экспериментирование с параметрами позволяют получить разнообразные вариации формирования центра тяжести треугольника с помощью циркуля и связанных с ним инструментов.
Вопрос-ответ

Как построить центр тяжести треугольника с помощью циркуля?
Для построения центра тяжести треугольника с помощью циркуля необходимо взять центр напрасной, проведенной через одну из вершин треугольника, и провести две дуги радиусом, равным половине длины стороны треугольника. Пересечение этих двух дуг даст нам центр тяжести треугольника.
Каком принципе основано построение центра тяжести треугольника с помощью циркуля?
Построение центра тяжести треугольника с помощью циркуля основано на принципе равенства площадей треугольников. Деление треугольника на три равные по площади части позволяет найти центр тяжести, который будет находиться на пересечении трех медиан треугольника. Таким образом, циркулем строятся дуги, равные половине длины стороны треугольника, и их пересечение дает искомую точку – центр тяжести треугольника.



