Математика всегда позволяет нам раскрыть тайны и загадки, проникнуть в глубины численных выражений и найти их истинное значение. Каждая формула, каждая функция имеют свои специфические особенности и логику, которую нужно разгадать. Одной из таких задач является определение результата функции log3 8.
Функция log3 8 является логарифмической функцией, где число 3 выступает в качестве основания логарифма, а число 8 - аргументом. Логарифм - это математическая операция, обратная возведению в степень. Она позволяет нам найти степень, в которую нужно возвести основание, чтобы получить аргумент. В данном случае, мы ищем, в какую степень нужно возвести число 3, чтобы получить число 8.
Чтобы найти результат функции log3 8, мы должны разложить число 8 на простые множители и выражить его через основание логарифма. Такой подход поможет нам найти истинное значение, скрытое за этой математической формулой. Проработаем каждый шаг, чтобы раскрыть это тайное число.
Разложение числа 8 по основанию 3 и способы его вычисления

В данном разделе мы рассмотрим основные аспекты разложения числа 8 по основанию 3, а также расскажем о нескольких способах его вычисления. Обратим внимание на то, что здесь мы не будем обсуждать простую операцию возведения числа в степень, а сфокусируемся на специализированной функции log3 8.
Что такое log3 8?
Logарифм на основании 3 от 8 означает степень, в которую нужно возвести число 3, чтобы получить число 8. Другими словами, это функция, выражающая значение показателя степени, при котором основание 3 возводится в этот показатель и равно числу 8.
Как вычислить log3 8?
Вычислить значение log3 8 можно с использованием различных методов. Один из возможных способов - применить свойство логарифма, согласно которому logb a = x эквивалентно тому, что число b возведенное в степень x равно числу a. Применяя это свойство к log3 8 = x, получим 3x = 8.
Таким образом, задача сводится к нахождению значения x, при котором 3 возводится в эту степень и даёт 8. В данном случае x будет равно 2, так как 32 = 9, а ближайшее к 8 число, которое можно представить в виде степени 3, это 32 = 9.
Другие методы вычисления log3 8
В дополнение к приведенному выше методу, существуют и другие пути вычисления log3 8. Например, можно использовать формулу замены основания логарифма:
log3 8 = log10 8 / log10 3
Также можно воспользоваться свойствами логарифма и преобразовать задачу к экспоненциальному виду, выражая log3 8 как 3x = 8.
Весьма интересным методом вычисления log3 8 является использование графика функции y = log3 x и определения точки пересечения этой функции с графиком y = 8. Таким образом, мы можем графически определить значение log3 8.
В конечном итоге, вычисление log3 8 зависит от выбранного метода и предпочтений пользователя. В данном разделе мы рассмотрели основы определения и вычисления этого логарифма, однако существуют и другие аспекты, которые могут быть интересными при изучении данного вопроса.
Понятие логарифма

В контексте логарифмической функции, результат log3 8 представляет собой значение степени, в которую нужно возвести число 3, чтобы получить число 8. Он показывает, что 8 является результатом возведения числа 3 в третью степень. Другими словами, log3 8 равен 3, поскольку 3 возводится в третью степень, что дает 8.
Логарифмы нашли широкое применение в различных областях науки и инженерии, таких как физика, экономика, статистика и компьютерные науки. Они помогают сократить сложные вычисления, решить уравнения и логические задачи, а также предоставляют ценную информацию о поведении и отношениях чисел и функций.
Понимание логарифма и его свойств позволяет нам более глубоко взглянуть на математику, расширить наши возможности в решении задач и лучше понять мир вокруг нас.
Краткое описание логарифма и его основные свойства
В данном разделе мы рассмотрим основные свойства и характеристики логарифма, включая его определение, особенности и примеры применения.
Логарифм - это математическая функция, обратная к возведению в степень. Он позволяет находить показатель степени, в которую нужно возвести заданное число, чтобы получить другое число.
Основная характеристика логарифма - основание, обозначаемое символом "a". Оно определяет, с помощью какой системы степеней будет производиться вычисление логарифма.
Свойства логарифма позволяют упростить выполнение его вычислений и решение математических задач. Одно из основных свойств - свойство смены основания, которое позволяет переходить от одного основания логарифма к другому. Также существуют свойства логарифма, связанные с операциями сложения и умножения.
Логарифмы широко используются в различных областях, включая физику, экономику, компьютерные науки и другие. Они помогают решать сложные математические задачи, моделировать процессы и оценивать вероятности.
Основание логарифма

Основания логарифмов могут быть как целыми, так и дробными числами. Чаще всего в математике используются натуральный логарифм с основанием e, двоичный логарифм с основанием 2 и десятичный логарифм с основанием 10. Каждое из этих оснований имеет свои особенности и применяется в различных областях науки и техники.
Натуральный логарифм с основанием e широко применяется в математике, физике и других естественных науках. Он обладает свойством преобразовывать сложные функции в более простые, что делает его незаменимым инструментом для решения сложных математических задач.
Двоичный логарифм с основанием 2 используется в информатике и вычислительной технике. Он позволяет оптимизировать работу с битами и бинарными данными, так как его значение указывает на количество бит, необходимых для представления числа.
Десятичный логарифм с основанием 10 широко используется в научных расчетах, инженерии, финансовой и бухгалтерской сфере. Он позволяет упростить вычисления с числами, так как его значение указывает на порядок числа и упрощает сравнение и анализ больших числовых данных.
Объяснение понятия основания логарифма и его значения для различных логарифмических функций

В данном разделе мы рассмотрим важное понятие основания логарифма и его значимость для различных логарифмических функций. Основание логарифма определяет, какая степень должна быть возведена в число, чтобы получить определенный логарифм. Основания логарифма могут быть различными и влиять на значения логарифмических функций.
Основание логарифма может быть представлено числом, обычно больше единицы, и указывает, во сколько раз основа возведена в некоторую степень, даст заданное значение логарифма. Наиболее распространенными основаниями являются 2, 10 и е, где е - основа натурального логарифма.
Изменение основания логарифма приводит к изменению значений логарифмических функций. Например, логарифм с основанием 2 будет иметь другие значения, чем логарифм с основанием 10. Отсюда следует, что выбор основания имеет решающее значение при решении уравнений и задач, связанных с логарифмическими функциями.
Кроме того, основание логарифма также влияет на свойства логарифмических функций, таких как изменение формы графика и свойства арифметических операций с логарифмами. Натуральный логарифм, имеющий основание е, обладает свойством упрощения и наиболее удобен для выполнения математических операций.
Что скрывается за числом 3 в логарифмическом выражении 8?

В математике, логарифмы оказываются очень полезными инструментами для решения различных задач, связанных с экспонентами и степенями. Они позволяют нам перейти от умножения и деления к сложению и вычитанию, что упрощает множество вычислений.
Один из наиболее распространенных типов логарифмов - это логарифмы по основанию 10, которые обозначаются как log. Но что значит выражение log3 8?
Здесь число 3 является основанием логарифма, а число 8 - аргументом, для которого мы ищем логарифм. Однако найти точное числовое значение этого логарифма не так просто. Чтобы ответить на вопрос, что представляет собой log3 8, нам необходимо рассмотреть основные свойства логарифма и применить их к данному выражению.
| Основные свойства логарифма |
|---|
| loga (xy) = loga x + loga y |
| loga (x/y) = loga x - loga y |
| loga (xn) = n * loga x |
С помощью этих свойств мы можем преобразовать выражение log3 8 в другую форму, которая может быть более удобной для вычисления или дальнейшего анализа. Однако точное значение log3 8 будет оставаться неизменным, и мы можем лишь приблизительно оценить его.
Таким образом, изучение выражения log3 8 позволит нам более глубоко понять, как работают логарифмы и как мы можем использовать их в различных математических задачах и моделях. Это знание может быть полезным для решения сложных проблем во многих областях науки и техники.
Объяснение и интерпретация записи log3 8

В данном случае, "log3 8" можно интерпретировать как значение показателя степени, при котором основание 3 должно быть возведено, чтобы получить число 8.
Интерпретация данного выражения может быть представлена как: "Какое число нужно возвести в степень с основанием 3, чтобы получить число 8?".
Вычисление "log3 8" может быть разложено на следующую формулу: "log3 8 = x", где "x" - неизвестное число, к которому основание 3 должно быть возведено, чтобы равняться 8.
Ответом на указанный вопрос будет число, равное 2, так как "3 в степени 2" равно 9, а "3 в степени 1" равно 3. Таким образом, "log3 8" равно 2.
Методы вычисления логарифма основания 3 от числа 8

- Метод замены основания: В этом методе мы заменяем указанное основание и искомое число на другое основание, с которым мы знакомы. В данном случае, мы можем заменить основание 3 на основание 2 или 10, и использовать уже известные нам логарифмы.
- Метод итераций: Этот метод основан на последовательном приближении к искомому значению логарифма. Мы начинаем с некоторого предположительного значения и уточняем его через несколько итераций, используя численные методы, такие как метод Ньютона или метод деления пополам.
- Метод таблицы логарифмов: Данный метод основывается на предварительно составленной таблице значений логарифмов. Мы ищем в таблице ближайшее значение для заданного числа, а затем используем интерполяцию для более точного определения логарифма.
Каждый из этих методов имеет свои преимущества и недостатки, и выбор метода зависит от конкретной ситуации и наличия доступных ресурсов. В следующих разделах мы более подробно рассмотрим каждый метод и приведем примеры их применения.
Рассмотрение различных методов подсчета значения log3 8 и сравнение их результатов

Этот раздел посвящен анализу различных способов вычисления значения log3 8 и сравнению полученных результатов. Мы представим соответствующие методы расчета и подробно исследуем их преимущества и недостатки.
Метод стандартного вычисления:
Один из способов вычисления значения log3 8 является стандартное применение математического определения логарифма. Этот метод требует знания основных математических свойств и законов логарифмов. Проведем вычисления и подробно изучим этот подход.
Метод десятичного логарифма:
Другой подход к вычислению log3 8 основан на использовании десятичного (обычного) логарифма. В этом методе мы преобразуем основание и аргумент логарифма к десятичной системе и используем свойства десятичного логарифма для получения ответа. Рассмотрим эту версию и проанализируем ее эффективность.
Метод применения математических функций:
Существует еще один способ подсчета значения log3 8, который включает использование математических функций. Мы можем воспользоваться функцией логарифмирования в калькуляторе или программе для нахождения точного значения. Изучим этот метод подробнее и проанализируем его достоинства и недостатки.
В данном разделе мы рассмотрели три различных метода вычисления значения log3 8 и сравнили их результаты. Каждый из этих подходов имеет свои достоинства и ограничения, поэтому выбор метода зависит от требуемой точности и доступности математических инструментов. Надеемся, что представленная информация поможет вам выбрать наиболее подходящий метод для вашего конкретного случая.
Графическое представление значения log3 8
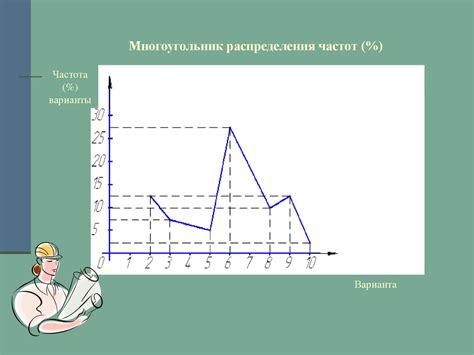
В данном разделе будет рассмотрено графическое представление значения log3 8, которое позволяет наглядно визуализировать эту математическую операцию. Отдельные точки на графике будут отображать соответствующие значения log3 8 и помогут лучше понять, как функция работает и какие результаты она дает.
log3 8 представляет собой значение, которое требуется найти с помощью логарифма по основанию 3 для числа 8. Число 8 можно представить в виде 3 в степени, которая удовлетворяет такому уравнению: 3^x = 8. Графическое представление log3 8 позволяет увидеть точку пересечения функции 3^x и числа 8 на графике.
Для наглядности на графике будут отмечены оси координат, на которых значения функции и числа будут отображаться. Анализируя график, можно понять, что результат log3 8 равен определенному числу, которое можно считать "степенью", с которой нужно возвести 3, чтобы получить 8. Обращаясь к графическому представлению, можно легче понять и запомнить значение log3 8 и использовать его для решения других математических задач.
Вопрос-ответ

Какой результат вычисления log3 8?
Результат вычисления log3 8 равен 2, т.е. 3 возводится в степень 2, чтобы получить 8.
Какая степень числа 3 равна 8?
Для того чтобы получить число 8, число 3 должно быть возводится во 2-ю степень, т.е. вычисление log3 8 даст результат равный 2.
Сколько троек нужно перемножить, чтобы получить 8?
Для того чтобы получить число 8, необходимо перемножить 2 тройки, т.к. 3 возводится во 2-ю степень, а вычисление log3 8 даст результат равный 2.
Каким числом нужно возвести 3, чтобы получить 8?
Для того чтобы получить число 8, число 3 должно быть возводится во 2-ю степень, т.е. результат вычисления log3 8 будет равен 2.



