Все мы встречались с различными математическими записями и символами в учебных пособиях, на досках в классе или в научных статьях. Они могут вызывать немалое количество вопросов и не всегда понятны с первого взгляда. Один из способов разобраться с этими записями - это изучение их значения и основополагающих теоретических концепций.
2n - одна из подобных записей, которая встречается в математике довольно часто. Ее значение может быть интерпретировано различными способами, но общая идея заключается в удвоении значения переменной n. Это понимание может быть полезно, когда необходимо решить задачу с двойным количеством элементов, удвоить значение или выполнить другие действия, основанные на удвоении.
Аналогично, запись n2 описывает квадрат значения переменной n. Такое значение может быть полезно во множестве задач, требующих расчета площадей или представления квадратичных зависимостей. Понимание значения этой записи позволит более эффективно использовать знания о квадратах чисел в различных областях математики и науки.
Еще одна часто встречающаяся запись - 3n2. Здесь мы имеем дело с кубической зависимостью значения переменной n. Используя это понимание, мы можем решить задачи, связанные с объемом, или описать поведение величин, подчиняющихся кубическому закону. Также это может иметь значение в контексте математических моделей и прогнозирования.
Наконец, мы рассмотрим запись 3co, которая относится к обратной трехмерной функции. Значение этой записи позволяет нам исследовать взаимосвязь между переменными, где изменение одной переменной вызывает обратные изменения другой переменной. Это полезное понимание при работе с обратными зависимостями в науке, экономике и других областях исследований.
Что такое запись 2n и как ее использовать в математике?

Запись 2n очень важна и широко применяется в математике. Она используется для описания числовых последовательностей, геометрических формул и других математических объектов. Эта запись позволяет упростить и обобщить сложные понятия, делая их более понятными и доступными для анализа и изучения.
В контексте математики, запись 2n представляет собой синтаксическую конструкцию, где число 2 умножается на переменную n. Здесь n может быть любым положительным целым числом или какой-либо другой переменной. Результатом выражения 2n является удвоенное значение переменной n.
Запись 2n может быть использована для решения различных математических задач, таких как нахождение значения функции в зависимости от значения переменной, построение графиков, манипуляции с числами и многое другое. Она позволяет упростить вычисления и сделать математические операции более удобными и понятными.
| Примеры использования записи 2n: |
|---|
| Если n = 3, то 2n = 2 * 3 = 6. |
| Если n = 5, то 2n = 2 * 5 = 10. |
| Если переменная n принимает последовательные значения 1, 2, 3, 4, 5, то соответствующие значения 2n будут 2, 4, 6, 8, 10. |
Таким образом, запись 2n является важным инструментом в математике, позволяющим упростить и обобщить различные математические понятия. Она может применяться в широком диапазоне математических задач и является полезным инструментом для ученых, инженеров и всех тех, кто работает с числами и формулами.
Отличия и применение записей n2 и 3n2 в математике

Отличие между записями n2 и 3n2 состоит в том, что в первом случае мы имеем только само число n в степени 2, тогда как во втором случае мы имеем число 3, умноженное на значение n, возведенное в квадрат.
- Запись n2 широко используется в математике для обозначения квадрата числа n. Она является удобным способом представления операции возведения в квадрат и может применяться в различных математических задачах и формулах.
- Запись 3n2 представляет собой умножение числа n, возведенного в квадрат, на коэффициент 3. Такая запись может использоваться, например, для расчета площади треугольника, где n представляет длину одной из сторон треугольника, а 3 - множитель для получения площади.
Выбор между использованием записи n2 и 3n2 зависит от контекста задачи и особенностей вычислений. В некоторых случаях может быть необходимо учесть множитель перед квадратом числа, а в других случаях достаточно просто возвести число в квадрат. Важно тщательно анализировать задачу и выбирать наиболее подходящий вариант записи в соответствии с требованиями и условиями задачи.
Применение в химии: роль соединения 3co в химических реакциях
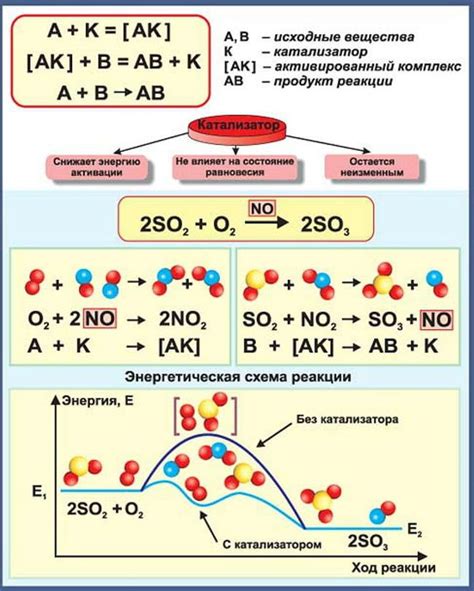
Соединение 3co представляет собой комбинацию трех атомов углерода и одного атома кислорода. Это соединение имеет уникальные свойства и интенсивно используется в различных процессах, связанных с образованием новых веществ и изменением состава химических соединений.
Одно из главных применений соединения 3co в химии - его использование в процессе окисления других веществ. Благодаря своей химической активности, 3co обладает способностью переносить электроны и участвовать в окислительно-восстановительных реакциях. Такое применение соединения находит широкое применение в промышленности и научных исследованиях.
Кроме того, соединение 3co играет важную роль в органической химии, где используется в процессе синтеза различных органических соединений. Благодаря своей химической структуре и свойствам, 3co может служить не только источником углерода и кислорода, но и катализатором для различных реакций. Это позволяет получать разнообразные органические соединения с высокой степенью чистоты и эффективностью.
Применение записи 3n2 в различных научных областях
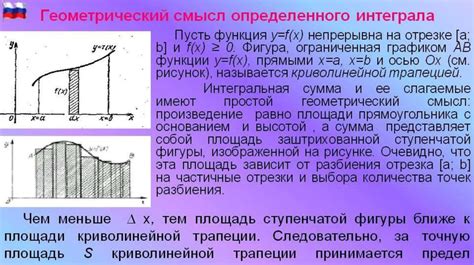
В данном разделе будет рассмотрено использование записи 3n2 в различных научных областях. Понимание и применение данной формулы имеет важное значение для получения и анализа данных в соответствующих исследованиях.
Запись 3n2 используется в многих областях науки, таких как математика, физика, химия, биология и другие. Эта формула позволяет выразить зависимость изменения величины от параметра, который представлен переменной n.
Результаты полученные с помощью записи 3n2 могут быть использованы для представления и анализа различных данных. Например, в математике обозначение 3n2 может использоваться для создания и применения различных моделей, предлагающих зависимости между двумя величинами.
В физике данная формула может служить для описания энергетических процессов и взаимодействия различных физических объектов. Она может быть использована для расчетов параметров системы и предсказания ее поведения в различных условиях.
В химии запись 3n2 может быть применена для анализа химических реакций и вычисления энергии активации. Она помогает изучать кинетику химических превращений и оптимизировать процессы в различных химических системах.
В биологии данная формула имеет свое применение в изучении генетических процессов и взаимосвязи между различными организмами. Она может помочь определить зависимости между фенотипическими признаками и генотипическими особенностями.
Таким образом, использование записи 3n2 в различных научных областях является неотъемлемой частью исследований. Эта формула предоставляет возможность не только описывать зависимости, но и проводить анализ данных, прогнозировать результаты экспериментов и совершенствовать теории в соответствующей научной области.
Сравнение и анализ примеров с использованием записей 2n, n2, 3n2 и 3co

В этом разделе мы рассмотрим четыре различных записи, которые возникают в математических и алгоритмических контекстах: 2n, n2, 3n2 и 3co. Мы проанализируем каждую запись и сравним их особенности и значения.
Первая запись 2n представляет собой удвоение значения переменной n. Она часто используется для описания роста функций и сложности алгоритмов. Например, если значение n увеличивается на 1, то значение 2n увеличивается в два раза. Такая запись позволяет легко оценивать рост функций.
Вторая запись n2 представляет собой квадрат значения переменной n. Эта запись часто используется для описания зависимости между двумя переменными в математических моделях и алгоритмах. Например, если значение n увеличивается на 1, то значение n2 увеличивается на квадрат.
Третья запись 3n2 представляет собой тройное произведение значения переменной n на ее квадрат. Эта запись может быть использована для описания роста функций и сложности алгоритмов, когда зависимость от n является более сложной, чем простое умножение на константу. Например, если значение n увеличивается на 1, то значение 3n2 увеличивается в 3 раза квадрата.
Четвертая запись 3co представляет собой тройное произведение значения константы c на куб переменной o. Эта запись может быть использована для описания менее распространенных математических моделей и алгоритмов, которые требуют более сложных зависимостей от переменных. Например, если значение o увеличивается на 1, то значение 3co увеличивается в 3 раза куба.
Таким образом, в данном разделе мы рассмотрели и сравнили четыре различные записи - 2n, n2, 3n2 и 3co, и изучили их значения и особенности использования. Каждая из этих записей имеет свою специфику и применение в математике и алгоритмах, и понимание их значений позволяет проводить более точные анализы и оценки.
Практические примеры и задачи для закрепления знаний о числах в различных записях

В данном разделе мы предлагаем рассмотреть практические примеры и задачи, которые помогут укрепить ваши знания о числах, записываемых в форматах 2n, n2, 3n2 и 3co. Решение данных задач поможет вам лучше понять специфику каждой записи числа и научиться использовать их в различных контекстах.
В таблице ниже представлены примеры задач, разбитые по типам записей чисел:
| Тип записи числа | Пример задачи |
|---|---|
| 2n | Вычислить значение 2n, где n = 5. |
| n2 | Найти квадрат числа n, где n = 7. |
| 3n2 | Определить результат выражения 3n2, если n = 4. |
| 3co | Рассчитать значение выражения 3co, где c = 6. |
Для каждой задачи предлагается составить алгоритм решения и вычислить значение числа в соответствии с его записью. Решение каждой задачи будет сопровождаться объяснением и пошаговым разбором, позволяющим лучше понять, как работает каждая формула.
Выполняя данные задачи, вы не только закрепите знания о записях чисел, но и разовьете навыки работы с различными форматами представления числовой информации. Это поможет вам применять эти знания в реальных задачах и задачах из других областей знаний.
Вопрос-ответ

Что означает запись 2n?
Запись 2n означает, что нужно умножить число n на 2. Например, если n = 3, то 2n будет равно 6.
Какое значение имеет запись n2?
Запись n2 означает, что число n нужно возвести в квадрат. Например, если n = 4, то n2 будет равно 16.
Что обозначает запись 3n2?
Запись 3n2 означает, что число n нужно возвести в квадрат, а затем результат умножить на 3. Например, если n = 2, то 3n2 будет равно 12.
Чем отличается запись 3n2 от записи 3co?
Запись 3n2 обозначает возвести число n в квадрат и умножить на 3, а запись 3co означает умножить число o на 3. В первом случае используется переменная n, а во втором - переменная o.
Какое значение имеет запись 3co?
Запись 3co означает, что число o нужно умножить на 3. Например, если o = 5, то 3co будет равно 15.
Зачем нужны записи 2n, n2, 3n2 и 3co?
Записи 2n, n2, 3n2 и 3co имеют большое значение в различных областях математики и программирования. Например, 2n представляет собой удвоенное значение переменной n, а n2 - квадрат этой переменной. А записи 3n2 и 3co используются в математических формулах и выражениях для расчета различных величин.



