В мире математики существует огромное количество формул, которые помогают нам вычислять различные значения. Одна из таких формул - это способ вычисления площади квадрата, когда известен его периметр. На первый взгляд может показаться, что решение данной задачи требует использования сложных и запутанных методов, однако на самом деле все гораздо проще, чем кажется.
Чтобы найти площадь квадрата, вам понадобится всего лишь несколько элементарных действий. Один из основных принципов математики заключается в поиске зависимостей между различными величинами, и в этом случае нет исключения. Если мы знаем периметр квадрата, то нам нужно определить его длину стороны, чтобы найти площадь. Продолжайте читать, чтобы узнать удивительный секрет поиска этого значения.
Приветствуем вас в мире геометрии и математических изысканий, где каждая проблема имеет свое уникальное решение. Наша сегодняшняя цель - найти площадь квадрата, зная только его периметр. Возможно, вам уже знакомы некоторые формулы для расчета площади квадрата, но что делать, когда известен только периметр? Здесь мы разгадаем это увлекательное головоломное задание и покажем, что математика - это искусство находить логические связи и решать сложные задачи.
Если вы готовы описать окружающий мир цифрами и доказать, что математика - неотъемлемая часть нашей повседневной жизни, тогда приступим к разгадке тайны поиска площади квадрата с известным периметром!
Метод 1: применение отношений сторон для вычисления площади квадрата

В данном разделе мы рассмотрим метод, основанный на использовании соотношений между сторонами квадрата для вычисления его площади. Мы представим вам простой способ расчета площади квадрата, используя только информацию о его периметре.
| Задано: | Периметр квадрата составляет 8 сантиметров. |
| Найти: | Площадь квадрата. |
Для начала, давайте вспомним, что периметр квадрата равен сумме длин всех его сторон. Если представить, что все стороны квадрата имеют одинаковую длину и обозначить её за 'x', то мы можем записать соотношение:
Периметр = 4 * x
Теперь у нас есть выражение для периметра квадрата. Чтобы вычислить площадь, нам необходимо найти длину стороны 'x' и затем возвести её в квадрат. Для этого мы можем использовать следующий шаг:
Площадь = x * x
Подставив выражение для периметра в формулу для площади, мы получим:
Площадь = (Периметр / 4) * (Периметр / 4)
Вычисляя эту формулу, мы получим значение площади квадрата, основываясь только на его периметре. В данном случае, для периметра 8 сантиметров, площадь квадрата будет равна:
Площадь = (8 / 4) * (8 / 4)
Площадь = 2 * 2
Площадь = 4 сантиметра квадратных
Метод 2: нахождение длины стороны квадрата и применение формулы площади
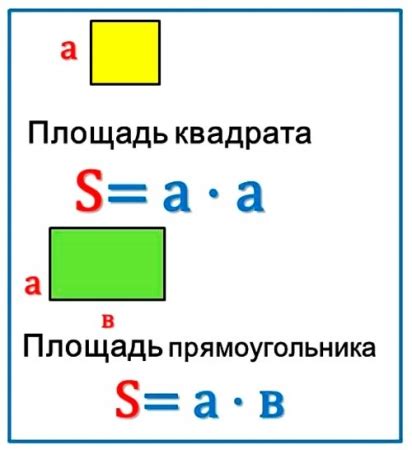
В данном разделе будет описан второй из двух методов вычисления площади квадрата, основанный на известном периметре. Мы сосредоточимся на нахождении длины стороны квадрата и применении формулы для вычисления его площади.
Для начала, давайте представим, что у нас есть квадрат с известным периметром в 8 см. Мы можем представить его состоящим из 4 одинаковых сторон, обозначим длину каждой стороны как "x". Таким образом, периметр будет равен 4x.
Чтобы найти длину стороны квадрата, мы можем разделить периметр на количество сторон. В данном случае, количество сторон равно 4, поэтому длина стороны будет равна периметру, деленному на 4: x = 8 / 4 = 2 см.
Теперь у нас есть значение длины стороны квадрата – 2 см. Для вычисления площади квадрата мы можем использовать формулу S = x², где S обозначает площадь, а x обозначает длину стороны. Подставляя известное значение, получим: S = 2² = 4 см².
Таким образом, площадь квадрата с периметром 8 см равна 4 см².
| Метод 1: нахождение периметра и применение формулы площади | Метод 2: нахождение длины стороны квадрата и применение формулы площади |
|---|---|
| Определение периметра квадрата и применение формулы для вычисления его площади. | Объяснение, как найти длину стороны квадрата с известным периметром и использование формулы площади для вычисления. |
Особенности расчета площади квадрата с общей длиной сторон в 8 сантиметров
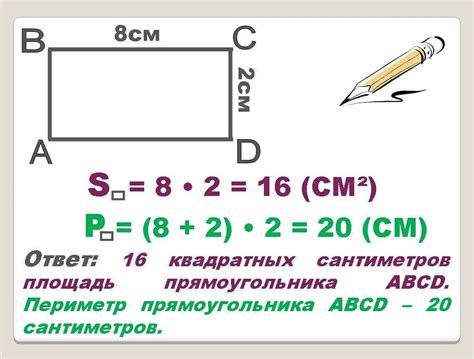
В данном разделе рассматриваются особенности определения площади квадрата с заданным периметром в 8 см. Мы обсудим уникальные нюансы и аспекты, важные для эффективного вычисления площади данной фигуры.
Уникальными характеристиками этого процесса являются не только заданный периметр в 8 см, но и принципы, которые лежат в основе данного вычисления. Некоторые из них могут оказаться необычными или неочевидными, поэтому важно углубиться в эту тему для полного понимания и правильного расчета.
В первую очередь, необходимо понять, что периметр квадрата – это сумма длин всех его сторон. В данном случае, когда периметр равен 8 см, каждая сторона будет иметь длину 2 см. Это означает, что мы имеем дело с маленьким квадратом, компактным и симметричным.
Теперь, когда у нас есть представление о фигуре, можно перейти к особенностям вычисления площади. Для вычисления площади квадрата, нужно возвести в квадрат длину любой его стороны. В нашем случае, каждая сторона равна 2 см, следовательно, площадь квадрата будет равна 4 квадратным сантиметрам.
Таким образом, для квадрата с периметром в 8 см определение его площади является простым и сводится к возведению в квадрат длины одной из его сторон. Понимание этих уникальных особенностей позволит легко рассчитать площадь данной геометрической фигуры и использовать полученные значения в дальнейших расчетах или измерениях.
Примеры решения задачи на нахождение площади квадрата с периметром 8 см

В этом разделе мы представим несколько примеров решения задачи, связанной с вычислением площади квадрата, имеющего периметр равный 8 см. Мы рассмотрим различные подходы и стратегии, которые помогут нам найти ответ на эту математическую задачу.
Пример 1: Воспользуемся знанием о свойствах квадрата. Мы знаем, что все стороны квадрата равны между собой. Исходя из этого, можно предположить, что периметр равен сумме длин всех сторон квадрата. Таким образом, если периметр равен 8 см, то длина одной стороны квадрата равна 8 см / 4 = 2 см.
Пример 2: Для нахождения площади квадрата, мы можем воспользоваться формулой площади квадрата, которая равна квадрату длины одной его стороны. Исходя из предыдущего примера, где длина одной стороны равна 2 см, мы можем легко найти площадь квадрата: 2 см * 2 см = 4 см².
Пример 3: Еще один подход заключается в использовании связи между периметром и площадью квадрата. Мы знаем, что периметр квадрата равен 4 умножить на длину его стороны. Таким образом, если периметр равен 8 см, то длина одной стороны квадрата равна 8 см / 4 = 2 см. Затем мы можем использовать найденную длину стороны, чтобы найти площадь квадрата по формуле: 2 см * 2 см = 4 см².
В данных примерах мы показали несколько различных способов решения задачи на нахождение площади квадрата с периметром 8 см. Это поможет нам лучше понять математические концепции и развить навыки решения подобных задач.
Вопрос-ответ

Какая формула позволяет вычислить площадь квадрата?
Формула вычисления площади квадрата - это сторона, возведенная в квадрат. То есть, площадь квадрата S равна a * a, где а - длина стороны квадрата.
Какой периметр квадрата с стороной 2 см?
Периметр квадрата можно вычислить, сложив длины всех его сторон. В данном случае, сторона квадрата равна 2 см, следовательно, периметр будет равен 2 + 2 + 2 + 2 = 8 см.
Как вычислить длину стороны квадрата с заданным периметром?
Для вычисления длины стороны квадрата с заданным периметром необходимо разделить периметр на 4. В данном случае, периметр равен 8 см, поэтому длина стороны будет равна 8 / 4 = 2 см.
Чему будет равна площадь квадрата с периметром 8 см?
Чтобы вычислить площадь квадрата с заданным периметром, необходимо найти длину его стороны. В данном случае, периметр равен 8 см, значит каждая сторона будет равна 8 / 4 = 2 см. Следовательно, площадь квадрата равна 2 * 2 = 4 см².
Можно ли использовать другую формулу для вычисления площади квадрата с заданным периметром?
Площадь квадрата всегда вычисляется по формуле a * a, где а - длина его стороны. Периметр не влияет на формулу вычисления площади квадрата. Таким образом, для вычисления площади квадрата с периметром 8 см, нужно найти длину его стороны и возвести ее в квадрат: 2 * 2 = 4 см².
Как вычислить площадь квадрата с периметром 8 см?
Чтобы вычислить площадь квадрата с периметром 8 см, нужно найти длину его стороны. Для этого периметр нужно разделить на 4, так как у квадрата все стороны равны. В данном случае, 8 см периметра поделим на 4, получим 2 см - это длина стороны квадрата. Далее, для вычисления площади квадрата нужно возвести в квадрат длину его стороны, то есть умножить 2 см на 2 см и получаем 4 см² - это и будет площадь квадрата с периметром 8 см.



