Четные числа являются важной концепцией в математике и широко применяются в различных областях науки и техники. Они представляют собой целые числа, которые делятся на 2 без остатка. Простым образом, четные числа можно выразить в виде удвоенного числа: 2, 4, 6, 8, 10 и так далее.
Какие свойства характеризуют четные числа? Во-первых, они обладают симметрией. Если мы возьмем любое четное число и разделим его пополам, то получим другое четное число. Например, 10 разделенное на 2 равно 5, а 5 умноженное на 2 равно 10. Это свойство важно при решении различных задач, таких как поиск среднего значения или разделение на равные группы.
Во-вторых, четные числа можно складывать и вычитать друг из друга без остатка. Например, 4 плюс 6 равно 10, а 10 минус 4 равно 6. Это позволяет использовать четные числа при решении задач, связанных с распределением ресурсов или определением паттернов в числовых рядах.
Четные числа также часто встречаются в природе. Например, многие животные имеют четное количество конечностей, а многие цветы имеют четное количество лепестков. Это является результатом эволюционного процесса и позволяет оптимизировать биологическую структуру.
Четные числа: определение и свойства

| Свойство | Пример |
|---|---|
| Делится без остатка на 2 | 4, 8, 16 |
| Можно разделить на 2 равные части | 10 = 5 + 5 |
| Являются четными степенями числа 2 | 22 = 4, 23 = 8 |
| Сумма двух четных чисел - четное число | 6 + 8 = 14 |
| Произведение двух четных чисел - четное число | 4 * 6 = 24 |
Четные числа широко используются в математике и программировании. В программировании, четные числа могут использоваться для упрощения алгоритмов и оптимизации работы программ.
Понятие четных чисел
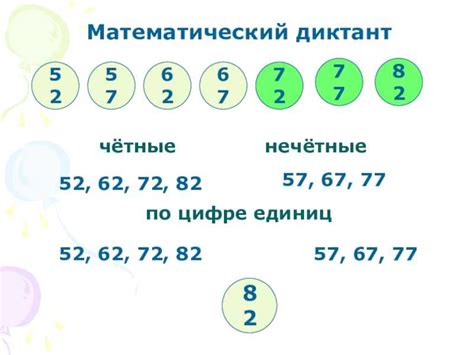
Например, числа 2, 4, 6, 8 и так далее - все они являются четными числами, поскольку они могут быть поделены на 2 без остатка.
Четные числа обладают рядом свойств:
- Сумма двух четных чисел всегда является четным числом.
- Произведение двух четных чисел также является четным числом.
- Если четное число умножить на 2, то получится число, одинаково четное с исходным числом.
Четные числа играют важную роль в математике и имеют множество приложений, например, в алгебре, геометрии и теории чисел.
Свойства четных чисел
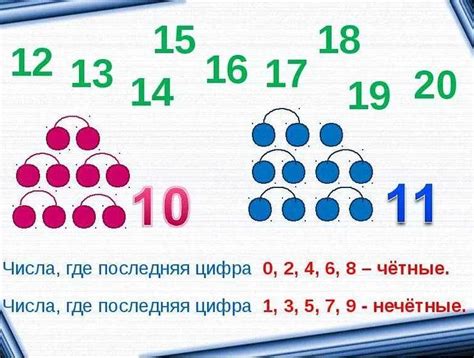
Четные числа обладают рядом уникальных свойств:
- Делятся на 2 без остатка. Это значит, что если четное число разделить на 2, то получится целое число без дробной части.
- Являются кратными числами. То есть, если число делится на 2, оно также является кратным числом.
- В сумме с другим четным числом всегда дают четное число. Если сложить два четных числа, то результат будет снова четным числом.
- Образуют арифметическую прогрессию. Это означает, что каждое следующее четное число отличается от предыдущего на 2.
- Могут быть представлены в виде произведения двух простых чисел. Например, число 14 можно представить как 2 * 7.
Свойства четных чисел значительно упрощают их анализ и могут использоваться в различных математических задачах и алгоритмах.



