В геометрии существует несколько методов разделения диагоналей прямоугольника на равные части. Два из них наиболее популярны и широко используются - это деление пополам и точка пересечения. Каждый из этих методов имеет свои преимущества и недостатки, их выбор зависит от конкретной задачи и целей, которых вы хотите достичь.
В методе деления пополам диагональ прямоугольника разделяется пополам в точке пересечения с противоположной стороной. Этот способ наиболее простой и понятный - он позволяет получить две равные по длине части диагонали. Благодаря этому, можно легко вычислить координаты точки пересечения и использовать их в дальнейших расчетах и измерениях.
С другой стороны, метод точки пересечения предлагает использовать особую точку, которая расположена на диагонали прямоугольника. При использовании этого метода, диагональ делится на две части в произвольном соотношении, что дает больше гибкости в расчетах. Это особенно полезно, когда требуется разделить диагональ на нестандартные пропорции или отношения.
Таким образом, выбор между делением пополам и точкой пересечения зависит от вашей конкретной задачи. Если вам необходимы равные части диагонали или вам требуется простой и понятный способ расчета, то деление пополам будет правильным выбором. Если же вам необходимо разделить диагональ на произвольные части с разными пропорциями, вам следует обратить свое внимание на метод точки пересечения.
Прямоугольник и его диагонали

У прямоугольника есть две диагонали - это отрезки, соединяющие противоположные углы фигуры. Диагональ прямоугольника является его характеристикой и может быть использована для решения различных геометрических задач.
Прямоугольник имеет две диагонали, которые делят его на четыре треугольника: два прямоугольных и два равнобедренных. Для прямоугольного треугольника длина диагонали может быть рассчитана с помощью теоремы Пифагора.
Если две диагонали прямоугольника равны по длине, то это значит, что прямоугольник является квадратом.
Рассмотрим вычисление длины диагоналей прямоугольника. Диагональ прямоугольника можно вычислить с помощью формулы: длина диагонали = корень квадратный из суммы квадратов длин сторон.
Точка пересечения диагоналей прямоугольника называется центром. Центр делит каждую диагональ пополам и является основой для построения описанной окружности прямоугольника.
Итак, диагонали прямоугольника имеют важное значение в геометрии и могут быть использованы для решения различных задач. Их длина и точка пересечения представляют интерес и позволяют получить дополнительную информацию о фигуре.
Основные понятия

Прямоугольник: это геометрическая фигура, у которой противоположные стороны равны и параллельны, а углы прямые.
Диагональ: это отрезок, соединяющий две вершины противоположных углов прямоугольника.
Перпендикуляр: это прямая, которая пересекает другую прямую под прямым углом.
Деление пополам: это разделение отрезка на две равные части.
Точка пересечения: это точка, в которой пересекаются две прямые или отрезка.
Точка пересечения диагоналей
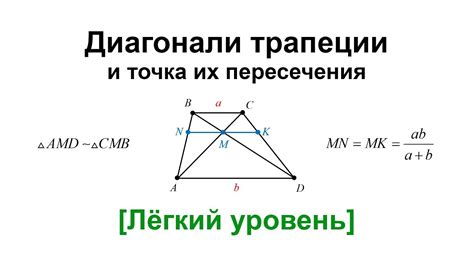
В прямоугольнике точкой пересечения диагоналей называется точка, в которой эти две линии пересекаются.
Рассмотрим прямоугольник со сторонами a и b. Диагонали этого прямоугольника делят его на четыре равные треугольные зоны. В точке пересечения диагоналей заключена площадь, равная половине площади всего прямоугольника.
Координаты точки пересечения диагоналей вычисляются по формуле:
| Координата x | Координата y |
|---|---|
| x = a/2 | y = b/2 |
Таким образом, точка пересечения диагоналей в прямоугольнике всегда имеет координаты (a/2, b/2).
Знание координат точки пересечения диагоналей может быть полезно при решении задач, связанных с разделением прямоугольника на две равные части или при определении центра симметрии прямоугольника.
Задачи на поиск точки пересечения

- Определение центра прямоугольника. Если известны координаты вершин прямоугольника, можно найти точку пересечения его диагоналей и использовать ее как центр.
- Расчет площади прямоугольника. Зная длины его диагоналей и зная, что они пересекаются в точке, можно использовать эту информацию для определения площади прямоугольника.
- Составление уравнения прямой. По двум точкам можно определить уравнение прямой, проходящей через них. Если известны координаты точки пересечения диагоналей и одной из вершин прямоугольника, можно составить уравнение прямой, проходящей через эти точки.
- Поиск угла между диагоналями. Если известны координаты точки пересечения диагоналей и координаты вершин прямоугольника, можно найти угол между диагоналями. Эта информация может быть полезна при решении задач, связанных с геометрией и механикой.
Задачи на поиск точки пересечения диагоналей прямоугольника имеют много различных вариаций и могут быть интересными для решения не только математикам, но и всем, кто интересуется геометрией и аналитической геометрией.
Преимущества использования точки пересечения

Использование точки пересечения диагоналей прямоугольника имеет несколько преимуществ:
- Одно из основных преимуществ - точка пересечения диагоналей делит их пополам. Это позволяет нам получить две равные и симметричные части прямоугольника, что может быть полезно при решении различных задач и конструкциях.
- Точка пересечения также служит важным ориентиром и опорной точкой для построения других линий или фигур в прямоугольнике. Например, если мы хотим построить окружность, проходящую через вершины прямоугольника, то точка пересечения диагоналей будет ее центром.
- При использовании точки пересечения диагоналей мы можем получить треугольники, которые имеют специальные свойства, например, будут прямоугольными или равнобедренными.
- Если для построения точки пересечения мы используем знания о координатах вершин прямоугольника, то это позволяет нам более точно определить положение и размеры прямоугольника, что может быть полезно при работе с графиками или разработке дизайна.
Таким образом, использование точки пересечения диагоналей прямоугольника является важным инструментом, который помогает в решении различных задач и может быть полезным при работе с геометрическими конструкциями.
Деление пополам: определение и особенности

Основная особенность деления пополам заключается в том, что диагональ прямоугольника всегда проходит через его центр. Это означает, что диагональ делит прямоугольник на два равных треугольника, а также на две равные прямоугольные половины.
Для определения длины или положения диагонали прямоугольника при помощи деления пополам, необходимо знать либо длину его сторон, либо размеры его прямоугольных половин. В зависимости от известных данных, можно использовать различные формулы и приемы для нахождения искомой величины.
Деление пополам является одним из простых и удобных методов определения диагонали прямоугольника. Благодаря своим особенностям, этот метод находит широкое применение в различных областях, таких как строительство, геометрия и дизайн.
| Преимущества деления пополам |
|---|
| Простота использования |
| Универсальность |
| Высокая точность результатов |
| Применимость к различным формам прямоугольников |
Определение диагонали, деление на равные части

Чтобы найти длину диагонали, можно использовать теорему Пифагора: диагональ, квадрат которой равен сумме квадратов сторон прямоугольника. Предположим, что длина прямоугольника равна a, а его ширина равна b. Тогда длина диагонали будет равна:
d = √(a² + b²)
Кроме того, диагональ прямоугольника делит его на две равные части, каждая из которых является прямоугольником. Для прямоугольника, чья длина равна a, а ширина равна b, диагональ разделит его на два прямоугольника, каждый из которых будет иметь длину a/2 и ширину b/2.
Сравнение двух методов

В данной таблице приведено сравнение двух методов нахождения точки пересечения диагоналей прямоугольника: деление пополам и использование формулы для нахождения координат точки пересечения.
| Метод | Преимущества | Недостатки |
|---|---|---|
| Деление пополам | Простота расчета | Не всегда точность |
| Точка пересечения | Точность расчета | Больше вычислений |
Метод деления пополам прост в реализации и не требует сложных математических вычислений. Однако, в некоторых случаях, он может не дать точного результата. Например, если прямоугольник имеет вытянутую форму или является искаженным, точность вычислений может снизиться.
Метод нахождения точки пересечения, основанный на формуле для нахождения координат точки пересечения двух прямых, обеспечивает более точные результаты. Однако, он требует выполнения дополнительных математических вычислений, что может занимать больше времени и ресурсов.
Выбор между этими двумя методами зависит от конкретной задачи и требуемой точности. Если точность не является критическим фактором, то метод деления пополам может быть предпочтительнее из-за своей простоты. Однако, для более точных результатов стоит использовать метод нахождения точки пересечения.
- Метод деления пополам проявляет себя как точный и надежный способ нахождения точки пересечения диагоналей прямоугольника.
- Метод нахождения точки пересечения через поиск точек противоположных углов прямоугольника также является эффективным и может применяться в ситуациях, когда необходимо найти точку пересечения без дополнительных вычислений.
- Оба метода дают одинаковый результат в случае, если прямоугольник является квадратом.
- В других случаях, метод деления пополам обеспечивает более точный результат, так как учитывает пропорциональные отношения диагоналей прямоугольника.
Рекомендации:
На основе проведенного исследования можно рекомендовать следующие действия при нахождении точки пересечения диагоналей прямоугольника:
- Если прямоугольник является квадратом, можно использовать любой из методов, так как они дадут одинаковый результат.
- Если приведение прямоугольника к квадрату не представляется возможным, рекомендуется использовать метод деления пополам для получения наиболее точного результата.
- В случае необходимости нахождения только координат точки пересечения без дополнительных вычислений, можно использовать метод поиска точек противоположных углов прямоугольника.



