График - это одна из базовых структур данных в информатике, которая представляет собой множество вершин и ребер, связывающих эти вершины. Графы используются для моделирования и анализа различных явлений и объектов, которые можно представить в виде связного множества элементов.
Графы являются незаменимым инструментом в различных областях информатики. Они применяются в алгоритмах, сетях, базах данных, компьютерной графике и многих других областях. С помощью графов можно решать задачи поиска кратчайшего пути, оптимизации, построения деревьев и многих других.
Графы могут быть направленными или ненаправленными, взвешенными или невзвешенными. Они могут иметь различные свойства и характеристики. Изучение и анализ графов позволяет разрабатывать эффективные алгоритмы и решать сложные задачи, связанные с моделированием и анализом различных систем и процессов.
График в информатике: что это такое?

Графики широко используются в информатике для решения различных задач, таких как поиск кратчайшего пути между вершинами, моделирование сетей, анализ социальных связей и многое другое. Важной особенностью графиков является их универсальность, так как они могут быть использованы для моделирования различных типов связей и отношений.
График состоит из вершин (узлов) и ребер (связей). Вершины представляют объекты или события, а ребра – связи между ними. Ребра могут быть направленными или ненаправленными, в зависимости от того, обязательно ли обратное направление связи.
Существуют различные способы представления графиков в компьютерной науке, включая матрицы смежности и списки смежности. Матрица смежности представляет график в виде таблицы, в которой строки и столбцы соответствуют вершинам, а ячейки указывают наличие или отсутствие связи между вершинами. Список смежности представляет график в виде списка, в котором каждый элемент списка представляет вершину и ее соседние вершины.
Использование графиков в информатике позволяет решать сложные задачи эффективно и элегантно. Они являются неотъемлемой частью алгоритмического мышления и компьтерной науки в целом.
Определение графика и его основные понятия
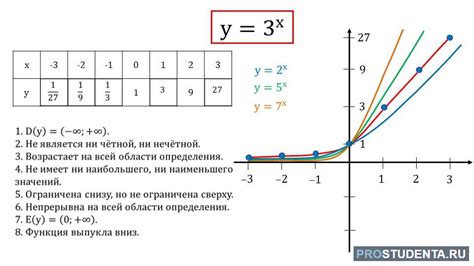
Вершина – это точка на графике, которая представляет собой отдельное значение или набор значений информации. Вершины могут быть отображены как точки, квадраты, круги и другие фигуры.
Ребро – это линия или кривая, которая соединяет вершины графика. Ребра показывают связи между значениями и могут иметь различную форму и толщину.
Оси координат – это горизонтальная и вертикальная линии, которые представляют собой систему координат на графике. Оси координат позволяют определить положение точек на графике и проводить измерения.
Масштаб – это отношение между размером отображаемых данных на графике и реальными значениями этих данных. Масштаб позволяет изменять детализацию и уровень деталей на графике.
Легенда – это ключ, который объясняет значения и символы, используемые на графике. Легенда обычно располагается в углу графика или указывается рядом с ним.
Угол наклона – это угол, под которым ребра графика соединяют вершины. Угол наклона может меняться в зависимости от целей анализа данных и предпочтений пользователя.
Точность – это мера того, насколько точно данные отображаются на графике. Чем выше точность, тем более точное и детализированное представление данных на графике.
Интерпретация – это процесс анализа и понимания данных на графике. Интерпретация помогает выявить закономерности, тренды и сравнить значения для принятия информированных решений.
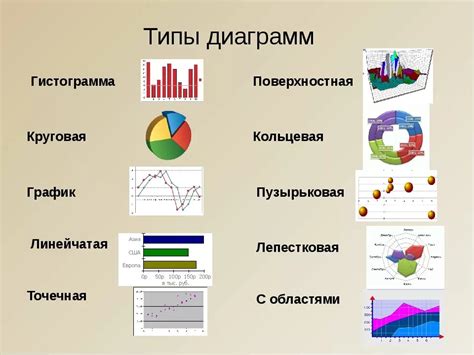
Типы графиков и их классификация

В информатике существует множество типов графиков, каждый из которых имеет свои особенности и применение. Графики помогают визуализировать данные и делать их более понятными и наглядными.
В зависимости от того, какие данные нужно отобразить, можно выделить следующие основные типы графиков:
- Линейный график: отображает изменение данных во времени и подходит для анализа тенденций и трендов.
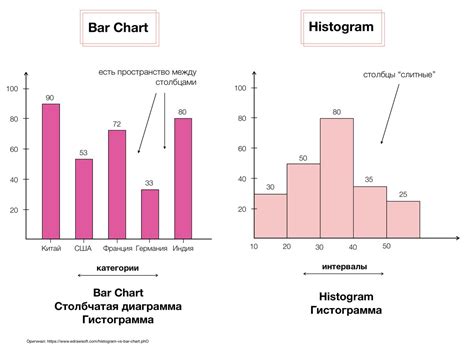
- Столбчатая диаграмма: позволяет сравнить значения разных категорий и выявить наиболее значимые.
- Круговая диаграмма: отображает соотношение частей к целому и позволяет выделить долю каждой категории.
- Облачная диаграмма: используется для визуализации связей и сходств между разными элементами.
- Гистограмма: позволяет определить распределение данных и выделить наиболее часто встречаемые значения.
Классификация графиков также зависит от вида данных, которые нужно отображать. Можно выделить следующие виды графиков:
- Статический график: представляет данные в виде неизменных графических объектов.
- Динамический график: обновляет данные в реальном времени и позволяет отслеживать их изменения.
- Интерактивный график: предоставляет пользователю возможность взаимодействовать со своими данными, изменять их и анализировать.
Выбор определенного типа графика зависит от поставленных задач и характеристик данных. Основная цель использования графиков - сделать информацию понятной и доступной для анализа, принятия решений и визуализации данных.
Применение графиков в информатике

Одним из ключевых применений графиков в информатике является анализ данных. Графики позволяют наглядно представить статистическую информацию и провести анализ данных. Например, график может показать зависимость между двумя переменными или визуализировать распределение данных.
Визуализация информации – еще одно важное применение графиков в информатике. Графики могут быть использованы для представления сложной информации в простой и наглядной форме, что позволяет лучше понять и запомнить представленные данные.
Графики также активно применяются в оптимизации процессов. Например, график производственного процесса может показать зависимость между временем и количеством произведенной продукции, что позволит оптимизировать процесс и улучшить его эффективность.
Важно отметить, что существует множество типов графиков, каждый из которых имеет свои особенности и применение. Некоторые из наиболее распространенных типов графиков в информатике включают линейные графики, круговые диаграммы, столбчатые диаграммы, точечные графики и другие.
| Примеры применения графиков в информатике: |
|---|
| Анализ данных и статистика |
| Визуализация информации |
| Оптимизация процессов |
Графики в анализе данных и визуализации
Графики играют важную роль в анализе данных и визуализации информации. Они позволяют наглядно представить сложные числовые структуры и помогают увидеть взаимосвязи между переменными.
Графики также используются в визуализации данных для презентации результатов исследований и демонстрации трендов и паттернов. От правильного выбора типа графика зависит понимание и восприятие информации. Например, диаграммы круга хорошо подходят для отображения доли каждой категории в общей сумме, а гистограммы – для сравнительного анализа значений различных переменных.
Преимущества использования графиков в анализе данных и визуализации очевидны: они помогают увидеть больше, лучше запомнить и быстрее понять информацию. Графики позволяют находить закономерности, выделять структуры и прогнозировать будущие тенденции, что делает их одним из наиболее мощных инструментов в руках исследователя.
| Тип графика | Описание | Пример использования |
|---|---|---|
| График линий | Показывает изменение переменной во времени | Отслеживание изменений цен акций на бирже |
| Диаграмма круга | Отображает долю каждой категории в общей сумме | Представление распределения населения по странам |
| Столбчатая диаграмма | Сравнивает значения различных переменных | Анализ продаж разных товаров в разных регионах |
| Круговая диаграмма | Показывает соотношение долей каждой категории | Изучение структуры затрат в бюджете компании |
Графики в компьютерной графике и играх

Графики имеют важное значение в компьютерной графике и играх. Они позволяют создавать виртуальные миры, реалистичные объекты и эффекты. Графики используются для отображения трехмерных моделей, текстур, освещения, анимации и многих других визуальных элементов.
Одно из главных применений графиков в компьютерной графике - это создание трехмерных моделей. Графики позволяют определить геометрию объектов, их форму, размеры и расположение в пространстве. Благодаря этому, разработчики могут создавать реалистичные и детализированные миры, в которых пользователи могут свободно перемещаться и взаимодействовать с объектами.
Также, графики используются для создания текстур - изображений, которые накладываются на поверхность объектов и позволяют им имитировать различные материалы и поверхности. Благодаря текстурам, объекты в играх и компьютерной графике выглядят более реалистично и привлекательно.
Освещение - еще одна важная функция графиков. Оно определяет, как объекты отображаются при разных условиях освещения, создавая реалистичные тени, отражения и другие эффекты. Благодаря освещению, объекты в играх и компьютерной графике приобретают объемность и глубину.
Наконец, графики играют важную роль в создании анимации. Они позволяют задавать различные позиции, формы и движения объектов для создания плавных и реалистичных анимаций. Благодаря графикам, объекты в играх и компьютерной графике могут двигаться, изменять свою форму и поведение в соответствии с заданными правилами и условиями.
Все эти возможности графиков делают их неотъемлемой частью компьютерной графики и игр. Благодаря графикам, разработчики могут создавать впечатляющие и невероятно реалистичные визуальные эффекты, которые захватывают воображение пользователей и позволяют им окунуться в виртуальные миры и приключения.
Графики в алгоритмах и структурах данных

Одно из распространенных применений графиков в алгоритмах - это поиск кратчайшего пути. Алгоритм Дейкстры и алгоритм Беллмана-Форда используют графики для нахождения кратчайшего пути между двумя вершинами взвешенного графа. Графики также используются для поиска минимального остовного дерева, например, с помощью алгоритма Прима или алгоритма Краскала.
Другим важным применением графиков является поиск потоков максимальной пропускной способности. Алгоритм Форда-Фалкерсона и алгоритм Эдмондса-Карпа используют графики для моделирования потоков и нахождения максимального потока в сети.
Графики также используются для решения различных задач комбинаторной оптимизации, таких как задача о назначении, задача о рюкзаке и задача о покрытии вершин.
Структуры данных, основанные на графиках, также широко применяются. Например, графы могут использоваться для хранения и обработки данных в базах данных. Графовые базы данных, такие как Neo4j, предлагают эффективные механизмы для работы с графиками, что позволяет выполнять сложные запросы и анализировать большие объемы данных.
| Применение | Алгоритм или структура данных |
|---|---|
| Поиск кратчайшего пути | Алгоритм Дейкстры, алгоритм Беллмана-Форда |
| Поиск минимального остовного дерева | Алгоритм Прима, алгоритм Краскала |
| Поиск потоков максимальной пропускной способности | Алгоритм Форда-Фалкерсона, алгоритм Эдмондса-Карпа |
| Решение задач комбинаторной оптимизации | Задача о назначении, задача о рюкзаке, задача о покрытии вершин |
Перспективы развития графиков в информатике
Графики в информатике играют важную роль в визуализации данных и представлении информации. Они позволяют наглядно отобразить сложные данные и сделать их более понятными для анализа и принятия решений. Вероятность того, что графики в информатике будут развиваться и прогрессировать в будущем, велика. Вот несколько перспектив развития графиков в информатике:
- Улучшение визуальных возможностей: С появлением новых технологий и программных инструментов разработчики смогут создавать более сложные и интерактивные графики. Это позволит визуализировать данные еще более наглядно и точно.
- Интеграция с большим объемом данных: С постоянным ростом объемов данных графики становятся все важнее в обработке и анализе данных. В будущем можно ожидать развития инструментов, которые будут способны обрабатывать и визуализировать еще больший объем данных.
- Развитие машинного обучения и искусственного интеллекта: Машинное обучение и искусственный интеллект играют все большую роль в обработке и анализе данных. В будущем можно ожидать развития интеллектуальных систем, способных автоматически создавать графики и выявлять закономерности в данных.
- Улучшение доступности и удобства использования: С появлением новых технологий разработчики смогут создавать более интуитивные и удобные в использовании инструменты для создания и визуализации графиков. Это сделает их доступными и понятными даже для людей без специальных навыков в области информатики.
В целом, графики в информатике имеют большие перспективы развития. Они играют важную роль в представлении данных и помогают наглядно отобразить сложные информации. С появлением новых технологий и программных инструментов можно ожидать развития более сложных и интерактивных графиков, способных обрабатывать и анализировать еще больший объем данных. Развитие машинного обучения и искусственного интеллекта также открывает новые возможности для использования графиков в информатике. Улучшение доступности и удобства использования сделает графики более доступными для широкого круга пользователей. Все это вместе обещает захватывающее будущее для графиков в информатике.



