Квадрат - это геометрическая фигура, которая имеет четыре равные стороны и четыре прямых угла. Он является простейшей и наиболее симметричной фигурой в геометрии. Более того, квадрат обладает рядом удивительных свойств и закономерностей, которые делают его изучение интересным и полезным для любого математика. Одним из таких свойств является изменение площади квадрата при увеличении его стороны.
Влияние увеличения стороны квадрата на его площадь
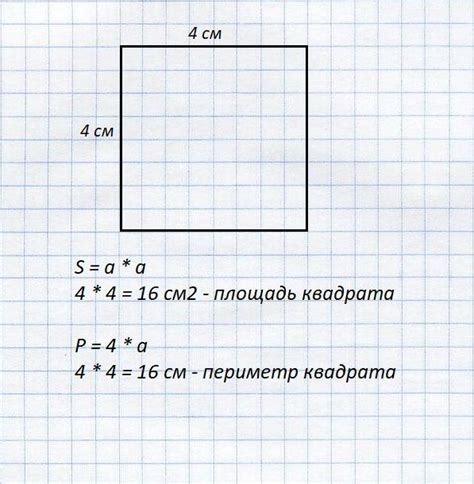
Если увеличить сторону квадрата на 3 см, то его площадь также изменится. Для того чтобы узнать, как изменится площадь, необходимо проделать следующие шаги:
- Узнать длину стороны квадрата до увеличения. Назовем эту величину "а".
- Увеличить значение "а" на 3 см.
- Возвести полученное значение в квадрат. Получим новую площадь квадрата.
Итак, пусть длина стороны квадрата до увеличения равна "а". Тогда новая площадь квадрата после увеличения стороны на 3 см будет равна (а + 3) * (а + 3).
Таким образом, увеличение стороны квадрата на 3 см приведет к изменению его площади по формуле (а + 3) * (а + 3), где "а" - длина стороны до увеличения. Площадь квадрата будет увеличиваться пропорционально увеличению длины его стороны.
Квадрат: изменение площади
Предположим, у нас есть квадрат со стороной 5 см. Для вычисления площади проведем следующую операцию: умножим 5 на 5, получим 25 см².
Теперь рассмотрим случай, когда сторона квадрата увеличивается на 3 см. Если исходная сторона равна 5 см, то после увеличения она станет равной 8 см (5 + 3). Для вычисления новой площади квадрата мы снова воспользуемся формулой: 8 умножить на 8. В результате получим 64 см².
Таким образом, при увеличении стороны квадрата на 3 см, площадь увеличивается с 25 см² до 64 см². Это значит, что площадь квадрата изменяется пропорционально изменению его стороны.
Как изменится площадь квадрата при увеличении одной стороны на 3 см?

При увеличении одной стороны квадрата на 3 см, его площадь также изменится. Чтобы понять, каким образом это произойдет, рассмотрим основные свойства квадрата.
Квадрат - это геометрическая фигура, у которой все стороны равны между собой. Площадь квадрата вычисляется по формуле: площадь = длина стороны в квадрате. То есть, площадь квадрата равна квадрату длины одной из его сторон.
Предположим, что длина стороны квадрата равна 'а'. Если увеличить эту сторону на 3 см, получим новое значение 'а+3'. Зная, что площадь квадрата равна квадрату его стороны, можно записать:
Старая площадь квадрата = а^2,
Новая площадь квадрата = (а+3)^2.
Раскрыв скобки во втором выражении, получим:
Новая площадь квадрата = а^2 + 6а + 9.
Из этих выражений видно, что новая площадь квадрата будет больше старой площади на величину, равную удвоенному значению увеличения стороны (6а) плюс квадрат увеличения стороны (9).
Таким образом, при увеличении одной стороны квадрата на 3 см, площадь квадрата увеличится на 6а + 9.



