Теоремы косинусов и синусов - это мощные математические инструменты, которые широко применяются в различных областях, особенно в геометрии и физике. Они позволяют решать различные задачи, связанные с треугольниками, и помогают определить длины сторон, величины углов и другие параметры треугольников.
Теорема косинусов используется для нахождения длины одной из сторон треугольника, если известны длины двух других сторон и величина включенного между ними угла. Эта теорема может быть особенно полезной, когда измерение сторон треугольника возможно, но измерение углов затруднено или невозможно.
Теорема синусов, с другой стороны, позволяет находить соотношение между длинами сторон и синусами величин углов треугольника. Она может использоваться для нахождения любой из сторон треугольника, если известны длины двух сторон и угол между ними.
Оба этих метода находят широкое применение в решении задач, связанных с геодезией, навигацией, физикой, инженерией и другими областями. Понимание того, когда и как применять эти теоремы, позволяет решать сложные задачи более эффективно и точно, и является важной навыком для специалистов в этих областях.
</p>
Теорема косинусов: основные понятия и формулы

Основные понятия и формулы, которые необходимо знать при использовании теоремы косинусов:
- Длина стороны треугольника обозначается маленькой буквой, например, "a", "b" или "c".
- Углы треугольника обозначаются заглавными буквами, например, "A", "B" или "C".
- Теорема косинусов формулируется следующим образом: квадрат длины одной стороны треугольника равен сумме квадратов длин двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
- Формула теоремы косинусов записывается как:
a^2 = b^2 + c^2 - 2bc * cos(A)(или аналогично для остальных сторон).
Применение теоремы косинусов полезно во многих задачах, таких как нахождение третьей стороны треугольника, нахождение угла по известным длинам сторон и многое другое.
Вычисление неизвестной стороны треугольника по двум известным сторонам и углу между ними
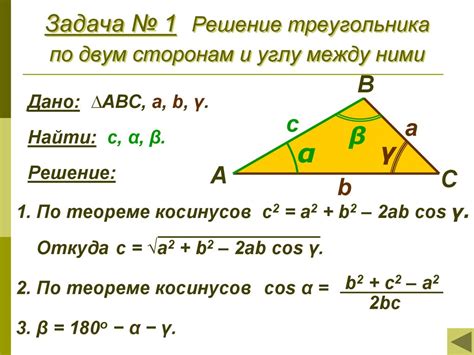
Одно из применений теоремы косинусов в геометрии заключается в возможности вычисления неизвестной стороны треугольника, если известны две другие стороны и угол между ними.
Для вычисления неизвестной стороны треугольника применяется следующая формула:
a^2 = b^2 + c^2 - 2bc * cos(A)
где:
- a - неизвестная сторона треугольника;
- b и c - известные стороны треугольника;
- A - угол между известными сторонами.
Для вычисления неизвестной стороны необходимо знать значение двух известных сторон и угол между ними. Затем можно подставить эти значения в формулу и выполнить несложные вычисления.
Применение теоремы косинусов позволяет решать задачи, связанные с построением и измерением треугольников в различных областях, таких как геометрия, физика, инженерия и многих других.
Однако, при использовании формулы теоремы косинусов необходимо учитывать, что она применима только для треугольников, в которых известны значения всех трех сторон или двух сторон и угла между ними. В противном случае, необходимо использовать другие методы для вычисления неизвестных величин.
Вычисление неизвестного угла треугольника по известным сторонам

Для вычисления неизвестного угла треугольника по известным сторонам можно использовать теорему косинусов.
Теорема косинусов гласит, что в треугольнике квадрат любой стороны равен сумме квадратов двух других сторон, умноженной на два произведения этих сторон и косинуса угла между ними.
Пользуясь этой теоремой, можно вычислить неизвестный угол треугольника следующим образом:
- Найдите значения всех известных сторон треугольника.
- Используя теорему косинусов, найдите значение косинуса неизвестного угла. Для этого подставьте значения известных сторон в формулу и решите уравнение относительно косинуса.
- Найдите арккосинус (обратный косинус) полученного значения косинуса. Это и будет значение неизвестного угла треугольника.
Помимо теоремы косинусов, можно использовать и теорему синусов для вычисления неизвестного угла. Однако, для этого необходимо знать либо две стороны и угол между ними, либо одну сторону и два угла. В случае, когда известны только стороны треугольника, теорема косинусов является более удобным и простым в использовании методом.
Применение теоремы косинусов в решении геометрических задач

Применение этой теоремы в решении геометрических задач может быть осуществлено следующим образом:
- Определите известные значения: длины двух сторон треугольника и косинус противолежащего угла.
- Используя формулу теоремы косинусов c^2 = a^2 + b^2 - 2ab * cos(C), вычислите значение третьей стороны.
- Проверьте, что вычисленное значение длины стороны неотрицательно.
Таким образом, применение теоремы косинусов в решении геометрических задач позволяет находить неизвестные стороны треугольников, используя известные значения других сторон и косинусов углов. Это очень полезный инструмент в различных областях, таких как ориентирование на местности, навигация, физика, архитектура и другие.
Примеры задач с использованием теоремы косинусов

Рассмотрим несколько примеров задач, в которых применяется теорема косинусов:
- Дан треугольник ABC, где AB = 5 см, BC = 7 см и угол C равен 30 градусов. Найдем длину стороны AC. Для этого воспользуемся теоремой косинусов:
- Дан треугольник XYZ, где XY = 8 см, YZ = 10 см и угол X равен 45 градусов. Найдем длину стороны XZ. Для этого воспользуемся теоремой косинусов:
- Дан треугольник PQR, где PQ = 6 см, QR = 4 см и угол P равен 60 градусов. Найдем длину стороны PR. Для этого воспользуемся теоремой косинусов:
C^2 = A^2 + B^2 - 2AB * cos(C)
C^2 = 5^2 + 7^2 - 2 * 5 * 7 * cos(30)
C^2 = 25 + 49 - 70 * 0.866
C^2 ≈ 74.59
C ≈ √74.59 ≈ 8.64
Таким образом, длина стороны AC примерно равна 8.64 см.
Z^2 = X^2 + Y^2 - 2XY * cos(Z)
Z^2 = 8^2 + 10^2 - 2 * 8 * 10 * cos(45)
Z^2 = 64 + 100 - 160 * 0.707
Z^2 ≈ 64 + 100 - 113.14
Z ≈ √50 ≈ 7.07
Таким образом, длина стороны XZ примерно равна 7.07 см.
R^2 = P^2 + Q^2 - 2PQ * cos(R)
R^2 = 6^2 + 4^2 - 2 * 6 * 4 * cos(60)
R^2 = 36 + 16 - 48 * 0.5
R^2 ≈ 36 + 16 - 24
R ≈ √28 ≈ 5.29
Таким образом, длина стороны PR примерно равна 5.29 см.
Таким образом, теорема косинусов является полезным инструментом для решения задач, связанных с измерением сторон треугольника и вычислением углов.
Расчет расстояния между двумя точками на плоскости с помощью теоремы косинусов

Для применения теоремы косинусов к расчету расстояния между двумя точками на плоскости, необходимо знать координаты этих точек. Предположим, что первая точка имеет координаты (x1, y1), а вторая точка - (x2, y2).
Для расчета расстояния между этими точками можно использовать следующую формулу:
d = sqrt((x2 - x1)^2 + (y2 - y1)^2)
Где d - расстояние между точками, sqrt - квадратный корень, (x2 - x1) - разность координат по оси X, (y2 - y1) - разность координат по оси Y.
Таким образом, применение теоремы косинусов позволяет легко и быстро вычислить расстояние между двумя точками на плоскости по их координатам.
Теорема синусов: основные положения и формулы

Основное положение теоремы синусов утверждает, что отношение длины стороны треугольника к синусу противолежащего ей угла постоянно и равно двум радиусам описанной окружности. Формула для данного отношения имеет вид:
a/sinA = b/sinB = c/sinC = 2R
где a, b и c - длины сторон треугольника, A, B и C - соответствующие этим сторонам углы, а R - радиус описанной окружности.
Также теорема синусов позволяет решать задачи на построение треугольников по известным данным. Например, если известны длины двух сторон треугольника и величина между ними заключенного угла, то можно найти длину третьей стороны или другой угол.
Использование теоремы синусов требует знания хотя бы трех известных величин - длины двух сторон треугольника и величины заключенного между ними угла. Для использования формулы также следует придерживаться определенных правил: длины сторон и углы должны быть в одних и тех же единицах измерения, углы должны быть измерены в радианах и быть меньше 180 градусов.
Таким образом, теорема синусов является важным инструментом для решения различных геометрических задач и построения треугольников по известным данным.
Применение теоремы синусов в решении треугольных задач

Одно из главных применений теоремы синусов - нахождение недостающих сторон или углов треугольника. Если известны две стороны и угол между ними, теорема синусов позволяет нам найти третью сторону или другие углы треугольника. Это свойство может быть полезно, когда требуется измерить расстояние до недоступных объектов или оценить размеры отдаленных объектов.
Еще одно применение теоремы синусов - нахождение площади треугольника. Если известны длины двух сторон и угол между ними, теорема синусов может быть использована для вычисления площади треугольника. Это может быть полезно, когда нужно определить площадь некоторой территории или вычислить объем фигуры, образованной треугольниками.
Теорема синусов также применяется для решения треугольных задач, когда известны только углы треугольника. Если известны все углы треугольника, теорема синусов позволяет найти соотношения между сторонами треугольника. Это может быть полезно при решении задач, связанных с геометрией или геодезией.



