Синус и косинус – две основные тригонометрические функции, которые широко применяются в различных областях науки и техники. Они играют важную роль в проекциях, позволяя определить геометрические свойства различных объектов и явлений.
Проекции – это способ представления трехмерных объектов и пространственных явлений на плоскости. Они используются в архитектуре, инженерии, географии, графике и других областях. Синус и косинус позволяют определить различные параметры проекций, такие как угол наклона, длина сторон, высота и другие характеристики.
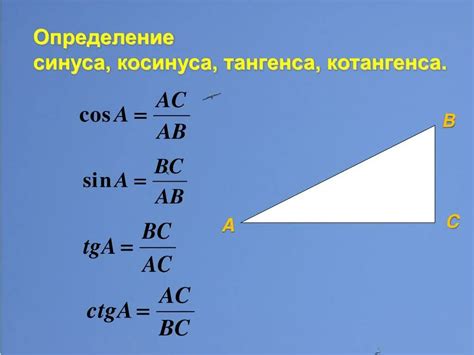
Синус и косинус связаны с одним из фундаментальных понятий геометрии – правильным треугольником. Синус угла треугольника равен отношению длины противоположной стороны к гипотенузе, а косинус – отношению длины прилежащей стороны к гипотенузе. Эти простые формулы позволяют вычислять синус и косинус для любого угла, а также использовать их для решения задач проекций.
Проекции: использование синуса и косинуса
Синус (sin) и косинус (cos) представляют собой отношение длины определенного отрезка к длине гипотенузы прямоугольного треугольника. В контексте проекций они позволяют определить координаты точек на плоскости.
Например, при использовании синуса и косинуса можно найти проекцию точки на ось X. Пусть у нас есть трехмерная точка с координатами (x, y, z). Если мы хотим найти ее проекцию на ось X, мы можем воспользоваться формулой:
x' = x * cos(a) + y * sin(a),
где x' - координата проекции на ось X, x - исходная координата точки по оси X, y - исходная координата точки по оси Y, a - угол между осью X и проекцией точки.
Аналогично, для проекции точки на ось Y используется следующая формула:
y' = -x * sin(a) + y * cos(a),
где y' - координата проекции на ось Y, x - исходная координата точки по оси X, y - исходная координата точки по оси Y, a - угол между осью Y и проекцией точки.
Таким образом, синус и косинус являются неотъемлемыми инструментами при работе с проекциями. Их использование позволяет более эффективно анализировать и визуализировать трехмерные объекты, делая задачи геометрии более доступными и понятными.
Определение проекций в геометрии

Существует несколько типов проекций, включая параллельные и центральные проекции. Параллельные проекции используются, когда объект проецируется на плоскость параллельно ей с сохранением размеров и формы объекта. Центральные проекции, с другой стороны, используются, когда объект проецируется из центральной точки или фокуса с изменением размеров и формы объекта.
Для определения проекций в геометрии можно использовать различные методы, включая использование синуса и косинуса. Синус и косинус - это тригонометрические функции, которые позволяют вычислить отношения сторон треугольника. Они широко используются в геометрии для определения углов, расстояний и проекций.
Например, при определении параллельной проекции можно использовать синус и косинус углов, чтобы вычислить координаты точек объекта на плоскости проекции. Это позволяет сохранить форму и размеры объекта в проекции.
В центральных проекциях синус и косинус также используются для вычисления координат точек объекта на плоскости проекции. Однако, в этом случае, размеры и форма объекта обычно изменяются.
Использование синуса и косинуса в проекциях позволяет точно определить положение и форму объекта на плоскости проекции. Это важный инструмент для проектировщиков, инженеров и архитекторов, помогающий создавать точные и реалистичные модели и иллюстрации.
Роль синуса в проекциях

Использование синуса в проекциях позволяет нам рассчитать эту длину. С помощью синуса мы можем найти противолежащий катет, который помогает нам определить, как далеко вдоль оси y или z находится объект от начальной точки. Таким образом, синус позволяет нам проецировать объекты на плоскости с учетом их вертикального или горизонтального положения.
Одним из распространенных примеров использования синуса в проекциях является построение трехмерных моделей на компьютере. Благодаря синусу мы можем создать иллюзию объемности и глубины объектов на двумерном экране. С помощью синуса мы можем изменить масштаб и перспективу объектов, чтобы они выглядели более реалистично и глубоко.
В целом, синус играет важную роль в проекциях, позволяя нам работать с различными аспектами проекции объектов на плоскость. Благодаря ему мы можем более точно и корректно отобразить объекты в двух и трех измерениях, создавая реалистичные и глубокие изображения.
Применение косинуса в проекциях

Когда мы имеем вектор и хотим найти его проекцию на ось, мы можем использовать косинус угла между вектором и выбранной осью. Для этого мы вычисляем скалярное произведение вектора и единичного вектора, направленного вдоль оси. Затем, умножив скалярное произведение на длину оси, мы получаем длину проекции вектора.
Формула для вычисления проекции вектора на ось:
Проекция = Длина вектора * Косинус угла между вектором и осью
Пример использования косинуса в проекциях:
- Пусть у нас есть вектор AB, длина которого равна 10 и который образует угол 60 градусов с осью X.
- Чтобы найти проекцию вектора AB на ось X, мы используем формулу:
- Проекция = 10 * cos(60°)
- Проекция = 10 * 0.5
- Проекция = 5
- Таким образом, длина проекции вектора AB на ось X равна 5.
Применение косинуса в проекциях позволяет нам определить как длину, так и направление проекции вектора на выбранную ось. Это важный инструмент при работе с геометрическими моделями и конструкциями, такими как рисунки, графики и трехмерные объекты.



