Дискриминант – это одно из важных понятий в алгебре и математике, которое помогает определить, сколько корней имеет квадратное уравнение. Обычно для нахождения дискриминанта необходимо знать значения всех коэффициентов - a, b и c. Однако, иногда у нас может отсутствовать значение коэффициента b. В таких случаях, можно воспользоваться специальной формулой, которая позволит найти дискриминант, пренебрегая коэффициентом b.
Возможность не учитывать коэффициент b возникает в тех случаях, когда у нас нет информации о его значении, а мы хотим узнать только количество корней уравнения. Для этого мы можем использовать следующую формулу:
D = a*c
В данной формуле мы пренебрегаем коэффициентом b и просто перемножаем значения коэффициентов a и c. Полученное значение даст нам информацию о типе корней уравнения.
Значение дискриминанта в квадратном уравнении

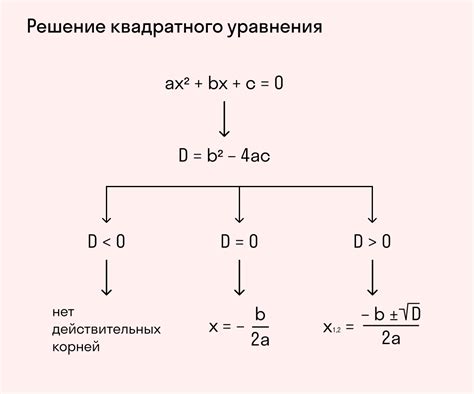
Значение дискриминанта находится по формуле D = b2 - 4ac, где a, b, c - коэффициенты квадратного уравнения.
Если дискриминант положительный (D > 0), то уравнение имеет два различных корня - x1 и x2.
Если дискриминант равен нулю (D = 0), то уравнение имеет один корень - x.
Если дискриминант отрицательный (D < 0), то уравнение не имеет действительных корней.
Понятие коэффициента b и его роль в уравнении

ax² + bx + c = 0
Коэффициент b является коэффициентом при переменной x, возведенной в первую степень. Он определяет, насколько велика линейная составляющая уравнения и влияет на его график и решения.
Коэффициент b может быть положительным, отрицательным или равным нулю. Если коэффициент b равен нулю, то линейная составляющая уравнения отсутствует, и уравнение принимает вид:
ax² + c = 0
При этом, решения уравнения можно найти без использования дискриминанта, просто решив квадратное уравнение вида ax² + c = 0.
Если коэффициент b не равен нулю, то линейная составляющая уравнения имеет влияние на его график и решения. Дискриминант квадратного уравнения, который рассчитывается по формуле:
D = b² - 4ac
позволяет определить, сколько и какие решения имеет уравнение.
Коэффициент b играет важную роль при изучении и решении квадратных уравнений. Он определяет, насколько сдвинут график уравнения по оси x и влияет на его форму и характер решений.
Как определить дискриминант в квадратном уравнении

Квадратное уравнение обычно имеет вид:
ax^2 + bx + c = 0Дискриминант является важным показателем при решении квадратного уравнения. Он определяет количество и тип корней. Дискриминант вычисляется с использованием следующей формулы:
D = b^2 - 4acГде D - дискриминант, b - коэффициент при x, и a и c - остальные коэффициенты уравнения.
Значение дискриминанта может принимать следующие значения:
| Значение | Тип корней |
|---|---|
| D > 0 | Два различных вещественных корня |
| D = 0 | Один вещественный корень |
| D < 0 | Два комплексных корня |
На основе значения дискриминанта D можно определить тип корней и продолжить решение квадратного уравнения в соответствии с полученным результатом.
Как найти дискриминант без учета коэффициента b

Однако, иногда возникает ситуация, когда известны только коэффициенты a и c, а значение коэффициента b отсутствует или неизвестно. В таком случае можно воспользоваться специальной формулой, чтобы вычислить дискриминант без учета коэффициента b.
Формула для вычисления дискриминанта без учета коэффициента b выглядит следующим образом:
Дискриминант (D) = a * c
Таким образом, чтобы найти дискриминант без учета коэффициента b, нужно перемножить значения коэффициентов a и c.
Полученное значение дискриминанта можно использовать для определения количества и типа корней квадратного уравнения. Если дискриминант положительный (D > 0), то уравнение имеет два различных вещественных корня. Если дискриминант равен нулю (D = 0), то уравнение имеет один вещественный корень. Если дискриминант отрицательный (D < 0), то уравнение не имеет вещественных корней (имеет два комплексных корня).
Теперь, имея формулу для вычисления дискриминанта без учета коэффициента b, вы сможете решать квадратные уравнения, даже если значение коэффициента b неизвестно или отсутствует. Не забывайте использовать эту формулу в сочетании с общей формулой для решения квадратных уравнений, чтобы получить точные значения корней.
Полезные формулы для решения квадратных уравнений

Дискриминант является ключевой величиной при решении квадратных уравнений. Он определяется по формуле:
Дискриминант (D) = b² - 4ac
где a, b и c - коэффициенты квадратного уравнения.
В зависимости от значения дискриминанта, квадратное уравнение может иметь различные типы решений:
- Если D > 0, то уравнение имеет два различных вещественных корня.
- Если D = 0, то уравнение имеет один вещественный корень, который является кратным.
- Если D < 0, то уравнение имеет два комплексных корня, которые являются сопряженными друг другу.
Если у квадратного уравнения известен только коэффициент a, а коэффициент b равен 0, то решение возможно без вычисления дискриминанта. В таком случае, формула для нахождения корней будет иметь следующий вид:
x₁ = -√(-c/a)
x₂ = √(-c/a)
Также обратите внимание, что в некоторых случаях квадратное уравнение можно привести к виду, в котором коэффициент b равен 0, путем применения тех или иных алгебраических преобразований.
Примеры вычисления дискриминанта без учета коэффициента b
Д = b^2 - 4ac
Однако иногда в уравнении отсутствует коэффициент b перед переменной x. В таких случаях вычисление дискриминанта производится без его учета.
Рассмотрим несколько примеров:
Пример 1:
Дано уравнение: 3x^2 - 12x = 0
Коэффициент a = 3, коэффициент c = 0. Коэффициент b отсутствует.
Вычислим дискриминант:
Д = 0^2 - 4*3*0 = 0
Пример 2:
Дано уравнение: 4x^2 - 8x + 4 = 0
Коэффициент a = 4, коэффициент c = 4. Коэффициент b также отсутствует.
Вычислим дискриминант:
Д = 0^2 - 4*4*4 = -64
Полученное значение дискриминанта меньше нуля, что означает, что у данного уравнения нет действительных корней.
Пример 3:
Дано уравнение: x^2 + 5 = 0
Коэффициент a = 1, коэффициент c = 5. Коэффициент b отсутствует.
Вычислим дискриминант:
Д = 0^2 - 4*1*5 = -20
Полученное значение дискриминанта также меньше нуля, следовательно, у данного уравнения нет действительных корней.



