Расчет площади фигуры – одна из основных задач геометрии, с которой сталкиваются не только ученики школы, но и потенциальные архитекторы, строители и дизайнеры. Очень часто возникает ситуация, когда известен только периметр фигуры, но необходимо найти ее площадь. В таких случаях есть несколько способов решения, но с определенной формулой это задание будет выполнено гораздо быстрее и проще.
Каждая фигура имеет свою уникальную формулу для расчета площади. Но существуют и такие задачи, когда необходимо найти площадь фигуры, зная только ее периметр. В таких случаях можно использовать универсальную формулу, которая подходит для разных фигур: площадь равна половине произведения периметра на радиус описанной окружности.
Итак, чтобы найти площадь фигуры по периметру, нужно сначала вычислить радиус описанной окружности. Для этого можно использовать формулу: радиус равен периметру фигуры, деленному на 2π.
Математический способ нахождения площади фигуры

- Площадь квадрата: Для нахождения площади квадрата необходимо умножить длину одной его стороны на саму себя. Формула для расчета площади квадрата: S = a^2, где S - площадь, а - длина стороны квадрата.
- Площадь прямоугольника: Площадь прямоугольника рассчитывается по формуле: S = a * b, где S - площадь, а и b - длины двух сторон прямоугольника.
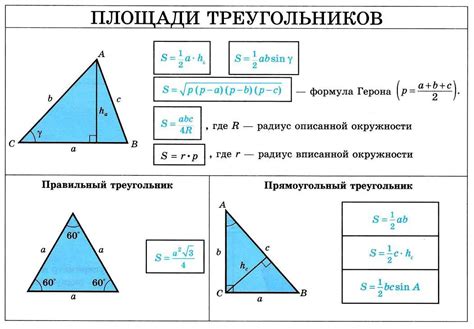
- Площадь треугольника: Существует несколько способов нахождения площади треугольника. Один из них - формула герона. Площадь треугольника по формуле герона можно вычислить, зная длины его сторон и полупериметр. Формула для расчета площади треугольника по формуле герона: S = √(p * (p - a) * (p - b) * (p - c)), где S - площадь, a, b и c - длины сторон треугольника, p - полупериметр (сумма длин всех сторон, деленная на 2).
- Площадь окружности: Площадь окружности рассчитывается по формуле: S = π * r^2, где S - площадь, π - математическая константа (приближенное значение 3,14159
Расчет площади треугольника по периметру и высоте
Для начала, нам нужно знать периметр треугольника. Периметр - это сумма всех сторон треугольника.
В общем виде, формула для расчета периметра треугольника выглядит следующим образом:
Периметр = a + b + c
Где a, b и c - длины сторон треугольника.
После того как мы знаем периметр треугольника, нам нужно найти его высоту. Высота треугольника - это отрезок, опущенный из вершины треугольника на противоположную сторону.
Как только мы найдем высоту треугольника, мы можем применить основную формулу для расчета площади треугольника:
Площадь = 0.5 * b * h
Где b - основание треугольника, а h - его высота.
Таким образом, для расчета площади треугольника по периметру и высоте, нам необходимо знать длины сторон треугольника, периметр и его высоту.
Длины сторон треугольника (a, b, c) Периметр Высота Площадь 5, 6, 7 18 4 12 3, 4, 5 12 3 6 8, 15, 17 40 7.5 30 Опираясь на эту таблицу, мы можем видеть, что при заданных длинах сторон треугольника, периметре и высоте, мы можем легко расчитать его площадь.
Обратите внимание, что для треугольников с разными длинами сторон, периметрами и высотами, площади также будут различными. Поэтому для каждого треугольника необходимо рассчитывать площадь отдельно, исходя из его параметров.
Способ определения площади прямоугольника по периметру
Формула для расчета площади прямоугольника по периметру и одной стороне выглядит следующим образом:
Площадь = (Периметр - 2 * (ширина + высота)) * (ширина / 2)
Для использования этой формулы вам необходимо знать периметр прямоугольника, а также значения любой его стороны. Подставьте эти значения в формулу и вычислите площадь прямоугольника.
Например, если у прямоугольника периметр равен 20, а одна сторона равна 4, то формула для расчета площади будет выглядеть следующим образом:
Площадь = (20 - 2 * (4 + высота)) * (4 / 2)
Далее вы можете выразить высоту прямоугольника и рассчитать его площадь. Это единственный неизвестный параметр, который можно легко найти.
Теперь вы знаете эффективный способ определения площади прямоугольника по его периметру. Используйте этот способ для быстрого и точного расчета площади.
Нахождение площади квадрата по его периметру
Формула для нахождения площади квадрата по его периметру проста и легко запоминается: Площадь = (Периметр/4) * (Периметр/4).
Для наглядности рассмотрим пример. Пусть у нас есть квадрат со стороной 12 единиц. Найдем его периметр: Периметр = 12 + 12 + 12 + 12 = 48. Затем подставим значение периметра в формулу: Площадь = (48/4) * (48/4) = 12 * 12 = 144.
Таким образом, площадь квадрата с периметром 48 единиц равна 144 квадратным единицам.
Этот метод нахождения площади квадрата по его периметру является крайне удобным и позволяет экономить время и усилия при решении геометрических задач.
Секретные формулы для расчета площадей некоторых фигур
Расчет площади фигуры может быть сложной задачей, но с использованием секретных формул, вы сможете легко и быстро получить нужный результат. Вот несколько формул для расчета площадей некоторых фигур.
Площадь квадрата:
Для расчета площади квадрата необходимо умножить длину его стороны на саму себя: S = a * a, где S - площадь квадрата, а - длина его стороны.
Площадь прямоугольника:
Формула для расчета площади прямоугольника: S = a * b, где S - площадь прямоугольника, а и b - длины его сторон.
Площадь треугольника:
Для расчета площади треугольника необходимо умножить длину его основания на высоту и разделить полученное значение пополам: S = (a * h) / 2, где S - площадь треугольника, а - длина основания, h - высота треугольника.
Площадь круга:
Формула для расчета площади круга: S = π * r^2, где S - площадь круга, π - число пи (около 3.14159), r - радиус круга.
Используя эти секретные формулы, вы сможете мгновенно вычислять площади различных фигур без особых проблем. Не забывайте, что точность результатов зависит от точности измерений, поэтому используйте хороший инструмент для измерения сторон фигур.