Когда мы сталкиваемся с задачей по поиску стороны квадрата по заданной площади, иногда может показаться, что это сложная задача. Однако, с помощью простых математических формул и немного логики, мы можем найти искомый ответ.
Первым шагом в решении этой задачи является понимание формулы для нахождения площади квадрата. Площадь квадрата определяется как произведение длины его стороны на саму себя. Исходя из этого, мы можем записать формулу: площадь = сторона × сторона, или S = a × a, где S - площадь квадрата, а a - длина его стороны.
Для того чтобы найти сторону квадрата по заданной площади, нам нужно найти квадратный корень из заданной площади. Квадратный корень обратный к возведению в квадрат, поэтому для нахождения стороны квадрата, мы должны взять квадратный корень из площади: a = √S, где a - искомая сторона квадрата, S - заданная площадь.
Теперь, когда мы знаем формулу и математическое выражение для нахождения стороны квадрата по площади, мы можем легко решить эту задачу. Просто подставьте заданную площадь S в формулу a = √S и вычислите корень. Результат будет являться стороной квадрата, соответствующей заданной площади.
Метод использования формулы

Чтобы найти сторону квадрата по известной площади, необходимо использовать следующую формулу:
Сторона квадрата = корень квадратный из площади
Для этого воспользуйтесь калькулятором или следующими шагами:
- Запишите известное значение площади квадрата.
- Используя калькулятор, найдите корень квадратный из этого значения.
- Результирующее число будет стороной искомого квадрата.
Например, если известна площадь квадрата равная 16 квадратных единиц, то сторона квадрата будет равна 4 единицы.
Этот метод прост и быстр, и поможет вам найти сторону квадрата по заданной площади без проблем.
Нахождение площади квадрата
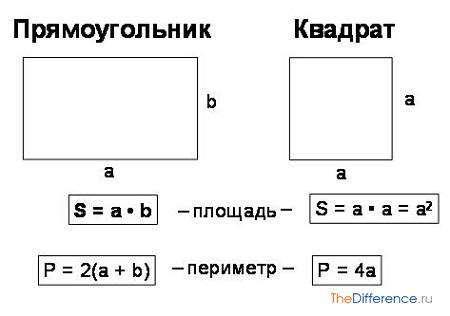
Если известна площадь квадрата и нужно найти длину его стороны, воспользуйтесь обратной операцией - извлечением квадратного корня. Для этого можно воспользоваться математическими функциями или калькулятором.
Таблица ниже приводит примеры нахождения площадей квадратов разных сторон:
| Длина стороны, a | Площадь, S |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
Из таблицы видно, что площадь квадрата возрастает в квадрате относительно его стороны. Например, при увеличении стороны с 1 до 2, площадь увеличивается в 4 раза (с 1 до 4).
Теперь, зная как найти площадь квадрата и обратную операцию, вы можете легко рассчитать площадь квадрата или найти его сторону при известной площади.
Как выразить сторону квадрата через площадь
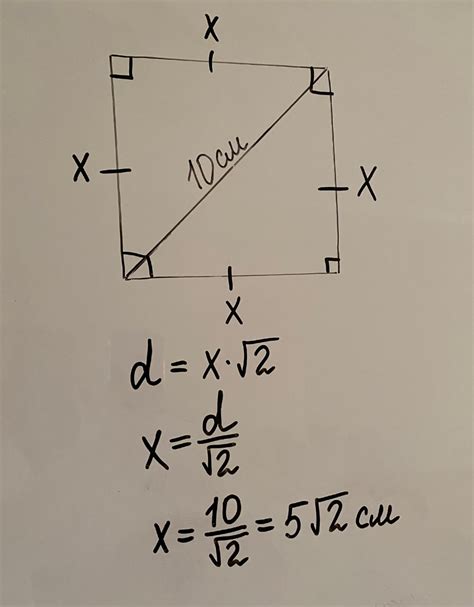
Для того чтобы найти сторону квадрата по его площади, необходимо использовать простую математическую формулу. Площадь квадрата вычисляется путем возведения его стороны в квадрат. Следовательно, чтобы найти сторону квадрата по его площади, достаточно извлечь корень из площади. При условии, что площадь известна, можно воспользоваться формулой:
Сторона = √Площадь
Применение этой формулы позволяет определить длину стороны квадрата, если известна его площадь. Например, если площадь равна 16 квадратным сантиметрам, для нахождения стороны квадрата можно воспользоваться формулой:
Сторона = √16 = 4 сантиметра
Таким образом, по заданной площади квадрата можно легко определить его сторону, применяя математическую формулу и извлекая корень из площади.
Вычисление квадратного корня из площади

Квадратный корень можно вычислить с помощью следующего алгоритма:
- Задаем значение площади (например, S = 25).
- Вычисляем квадратный корень из площади с помощью формулы: сторона = √S.
- Получаем значение стороны квадрата (например, сторона = √25 = 5).
Например, для квадрата с площадью 25 квадратных единиц сторона будет равна 5 единицам.
Таблица ниже демонстрирует вычисление квадратного корня из различных площадей квадратов:
| Площадь (S) | Квадратный корень (√S) | Сторона |
|---|---|---|
| 16 | 4 | 4 |
| 36 | 6 | 6 |
| 49 | 7 | 7 |
Таким образом, вычисление квадратного корня из площади поможет нам определить сторону квадрата.
Как найти сторону квадрата посредством математических функций
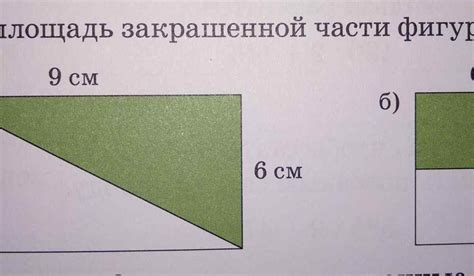
Если вам нужно найти сторону квадрата по заданной площади, вы можете воспользоваться следующей математической формулой:
| Шаги | Формула |
|---|---|
| 1 | Найдите квадратный корень из площади, чтобы получить длину стороны. |
| 2 | Запишите полученное значение в качестве ответа. |
Например, если у вас есть квадрат со стороной в 25 квадратных единиц, чтобы найти длину стороны, вы должны взять квадратный корень из 25, что равно 5. Таким образом, сторона квадрата равна 5 единицам.
Используя эти математические функции, вы сможете легко и точно найти сторону квадрата по заданной площади без необходимости выполнять сложные вычисления.
Использование калькулятора для площади и стороны квадрата

Если вам нужно найти сторону квадрата по известной площади, вы можете воспользоваться калькулятором для упрощения этого процесса. Калькулятор позволяет вам ввести известную площадь и получить результат в виде значения стороны квадрата.
Чтобы воспользоваться калькулятором, следуйте простым шагам:
- Откройте калькулятор, предназначенный для вычисления стороны квадрата по площади.
- Введите значение известной площади в указанное поле на калькуляторе.
- Нажмите кнопку "Вычислить" или аналогичную кнопку на калькуляторе, чтобы получить результат.
После выполнения этих шагов калькулятор выведет значение стороны квадрата, соответствующее введенной площади. Вы можете использовать этот результат для своих дальнейших вычислений или задач.
Важно помнить, что введенные значения должны соответствовать заданной единице измерения. Например, если площадь задана в квадратных метрах, результат будет выведен также в метрах.
Использование калькулятора для площади и стороны квадрата позволяет сэкономить время и упростить процесс вычисления. Это особенно удобно, когда вам нужно найти сторону квадрата по известной площади и вам необходимо быстро получить результат.



