Одной из важнейших задач в программировании является правильное управление переменными. Отправной точкой в этом процессе является понимание независимости значения переменной. Такая независимость позволяет осуществлять более гибкое и контролируемое управление данными.
Если переменная зависит от другой переменной, то ее значение будет изменяться в соответствии с изменениями другой переменной. Однако, независимость значения переменной достигается тогда, когда значение переменной не зависит от каких-либо других факторов или переменных.
Основными критериями независимости значения переменной являются:
- Отсутствие прямых зависимостей - значение переменной не должно зависеть от других переменных, а должно быть установлено независимо от них.
- Отсутствие косвенных зависимостей - значение переменной не должно зависеть от результатов выполнения других операций или функций.
- Стабильность - значение переменной не должно меняться в процессе работы программы, если только это не является необходимым условием для ее корректной работы.
Правильное определение и контроль независимости значения переменной в выражении является важным аспектом программирования, позволяющим создавать более надежные и эффективные программы.
Критерии независимости значения переменной

Существует несколько критериев, которые помогают определить независимость значения переменной:
- Отсутствие зависимости от других переменных: Независимая переменная не зависит от значений других переменных. Это означает, что изменение значения другой переменной не приводит к изменению значения независимой переменной. Например, если переменная "x" зависит только от константы "5" и не зависит от каких-либо других переменных, то "x" является независимой переменной.
- Отсутствие зависимости от времени: Независимая переменная не зависит от времени выполнения программы. Это означает, что значение независимой переменной остается постоянным независимо от временных условий или изменений в программе.
- Отсутствие зависимости от внешних факторов: Независимая переменная не зависит от внешних факторов или внешнего окружения. Она не должна быть связана с пользовательскими вводами, файлами, сетевыми соединениями или другими внешними факторами.
- Отсутствие влияния на другие переменные: Независимая переменная не оказывает влияния на значения других переменных в выражении. Это значит, что изменение значения независимой переменной не приводит к изменению значений других переменных, участвующих в выражении.
Определение независимости значения переменной играет важную роль в программировании, так как позволяет более точно управлять значениями переменных и предотвращать ошибки при выполнении выражений и алгоритмов.
Как узнать, что значение переменной независимо от контекста?

Есть несколько критериев, по которым можно оценить, что значение переменной независимо:
- Постоянное значение: если значение переменной не меняется во время выполнения программы и остается постоянным, то можно утверждать, что оно независимо от контекста. Например, если переменная
xвсегда равна 5, независимо от внешних факторов, то можно сказать, что значениеxнезависимо. - Отсутствие зависимых от других переменных: если значение переменной не зависит от значений других переменных, то оно также является независимым. Например, если значение переменной
yзависит только от значенияxи не зависит от значений других переменных, то можно утверждать, что значениеyнезависимо. - Константное значение при любом контексте: если значение переменной остается постоянным независимо от любого контекста, то оно также считается независимым. Например, если переменная
zдолжна иметь значение 10 в любом состоянии программы, то можно утверждать, что значениеzнезависимо.
Важно понимать, что для каждой переменной может быть свой набор критериев независимости, и они будут зависеть от конкретной программы или ситуации.
Зная, что значение переменной независимо от контекста, мы можем быть уверены в ее постоянстве и использовать это значение при дальнейших вычислениях или операциях.
Методы проверки независимости значения переменной

1. Корреляционный анализ
2. Анализ дисперсии
Данный метод позволяет сравнить вариабельность значений переменной при различных уровнях других факторов. Если различие между средними значениями переменной на разных уровнях фактора не является статистически значимым, то можно считать, что переменная независима от данного фактора.
3. Регрессионный анализ
Данный метод позволяет оценить, как одна переменная влияет на другую. Если коэффициент регрессии равен 0, то можно считать, что переменная независима от влияющей переменной. Если коэффициент отличен от 0, то имеется статистически значимая зависимость.
Важно помнить, что результаты проверки независимости переменной могут зависеть от выбора метода и данных, поэтому рекомендуется проводить несколько анализов для получения более точного результата.
Тестирование переменной на независимость

Для определения независимости значения переменной в выражении необходимо провести тестирование. Тестирование переменной на независимость позволяет выяснить, какое количество и какие значения переменной могут быть использованы в выражении, при этом не влияя на результат.
Тестирование переменной на независимость включает в себя проведение различных экспериментов, в ходе которых проверяется влияние изменения значения переменной на результат выражения. Следующая таблица показывает примеры тестирования переменной X на независимость в выражении Y = X^2 + 3:
| X | Y |
|---|---|
| 1 | 4 |
| 2 | 7 |
| 3 | 12 |
В данном примере видно, что изменение значения переменной X влияет на результат выражения Y. Значит, переменная X зависит от значения Y. Для того чтобы переменная была независима, изменение ее значения не должно влиять на результат выражения.
Тестирование переменной на независимость является важной частью анализа выражений, так как свободные переменные могут влиять на результат и алгоритмы работы программы. При правильном тестировании можно выявить и устранить ошибки, связанные с независимостью переменных, и повысить надежность программы.
Критерий независимости переменной

Главным критерием независимости переменной является то, что переменная не должна зависеть от другой переменной или источника. Если переменная является независимой, то изменение её значения не будет приводить к изменениям в значениях других переменных или источниках.
Для определения независимости переменной, можно использовать следующие критерии:
- Статистический критерий: проводится статистический анализ и вычисляются показатели значимости и корреляции.
- Экспертный критерий: основывается на мнении и опыте эксперта в данной области. Эксперт может оценить, насколько переменная может быть независимой.
- Практический критерий: основывается на практических исследованиях или опыте работы с данной переменной. Если результаты исследований или опыт работы свидетельствуют о независимости переменной, то она считается независимой.
Необходимо учитывать, что независимость переменной может быть относительной. Это значит, что переменная может быть независимой в определенных условиях, но зависимой в других. Поэтому, при оценке независимости переменной необходимо также учитывать контекст и условия исследования.
Критерий независимости переменной является важным инструментом при анализе данных и позволяет установить достоверность и объективность результатов исследования.
Имеет ли значение переменной влияние на результат

В некоторых случаях результат вычисления выражения зависит от значения переменной. Например, рассмотрим следующий код:
int x = 5;
int y = x + 10; В этом примере переменная x имеет значение 5, и значение переменной y будет равно 15. Если бы значение переменной x было другим (например, x = 2), то значение переменной y также было бы другим (y = 12).
Однако, есть и такие случаи, когда значение переменной не влияет на результат выражения. Рассмотрим пример:
int a = 5;
int b = 10;
int c = a + b; В этом примере значения переменных a и b не влияют на результат сложения. Результат будет всегда равен 15, независимо от конкретных значений переменных a и b.
Таким образом, влияние значения переменной на результат выражения зависит от самих выражений и алгоритмов, которые используют эти переменные. Важно правильно анализировать свои программы и понимать, когда и какие переменные влияют на результат.
Доверительный интервал значения переменной

Для расчета доверительного интервала необходимо учитывать выборку данных и уровень доверия. Выборка данных представляет собой подмножество из генеральной совокупности, которая содержит все возможные значения переменной. Уровень доверия определяет степень уверенности, с которой мы можем утверждать, что искомая величина находится в расчетном интервале.
Для расчета доверительного интервала используются различные статистические методы, такие как Z-критерий и t-критерий. Z-критерий применяется при больших выборках или когда известна истинная дисперсия генеральной совокупности, в то время как t-критерий используется при малых выборках или когда истинная дисперсия неизвестна.
Итак, доверительный интервал значения переменной выражается в виде двух чисел - нижней и верхней границы диапазона. Например, если мы получили доверительный интервал (1.5, 4.2) с уровнем доверия 95%, это означает, что с вероятностью 95% искомая величина находится в интервале от 1.5 до 4.2.
Примеры независимых переменных

- Возраст: выбранное значение не зависит от других переменных, таких как пол или национальность.
- Цвет глаз: цвет глаз не зависит от других характеристик, таких как волосы или рост.
- Образование: уровень образования не зависит от возраста или занятости.
- Политические взгляды: выбор политических взглядов не зависит от возраста или дохода.
- Географическое местоположение: местоположение не зависит от рода деятельности или образования.
Эти примеры независимых переменных показывают, что значение переменной может быть стабильным и не зависеть от других факторов. Определение и распознавание независимых переменных помогает в проведении комплексного анализа и исследования.
Значение переменной в контексте
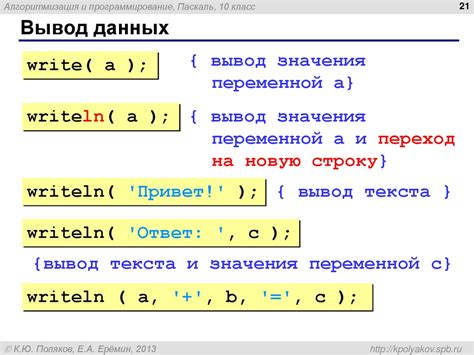
Когда переменная имеет постоянное значение и не зависит от внешних факторов, ее называют независимой переменной. В этом случае, значение переменной остается неизменным на протяжении всего выражения.
Однако, в некоторых случаях значение переменной может изменяться в зависимости от контекста. В этом случае, переменная называется зависимой переменной. Зависимая переменная может принимать различные значения в зависимости от условий, функций или других переменных, участвующих в выражении.
Чтобы определить, является ли переменная зависимой или независимой в выражении, необходимо анализировать контекст, в котором она используется. Это включает в себя анализ условий, какие значения принимают другие переменные, а также функции или операции, которые используются в выражении.
Важно отметить, что зависимость или независимость переменной может меняться в различных ситуациях. Например, переменная может быть независимой в одной части выражения, но стать зависимой в другой части. Поэтому при анализе выражения необходимо учитывать каждое использование переменной.
| Пример | Значение переменной | Зависимость |
|---|---|---|
| if (x > 5) | x = 7 | зависимая |
| else | x = 3 | зависимая |
| if (y > 10) | y = 12 | независимая |
В таблице приведен пример, где переменная x является зависимой, так как ее значение зависит от условия (больше 5 или меньше 5). При этом переменная y является независимой, так как ее значение не зависит от условий.
Итак, значение переменной в контексте является важным фактором для определения ее независимости в выражении. Анализ контекста, включая условия, функции и другие переменные, поможет определить, является ли переменная зависимой или независимой.



