Пересечение графиков функций - это момент, когда две функции имеют общую точку на координатной плоскости. Определить пересечение графиков можно с помощью аналитических методов или графическим способом.
Аналитический метод подразумевает решение системы уравнений, составленной из функций, что может быть достаточно сложной задачей. Однако, если функции имеют простой вид, то этот метод можно применить без особых проблем. Для этого необходимо приравнять две функции между собой и решить полученное уравнение.
Графический способ заключается в построении графиков функций на координатной плоскости и определении точек их пересечения. Для этого необходимо нарисовать оси координат, построить графики двух функций и найти их пересечение. Если графики пересекаются, то функции имеют общую точку, если нет - то пересечения нет.
Определение пересечения графиков функций может быть полезным инструментом при анализе различных математических задач и моделей. Этот навык может найти применение в таких областях, как физика, экономика, статистика, компьютерное моделирование и многих других.
Пересечение графиков функций: основные методы

Метод подстановки:
Один из самых простых и распространенных методов определения пересечения графиков функций заключается в использовании метода подстановки. Он состоит в замене значения переменной в одной функции на значение переменной в другой функции и последующем решении полученного уравнения.
Метод графического представления:
Этот метод основан на графическом представлении графиков функций и позволяет наглядно определить точки их пересечения. Для этого необходимо построить графики функций на одной координатной плоскости и обратить внимание на точки их пересечения.
Метод аналитического решения:
Данный метод используется для аналитического решения системы уравнений, полученной из графического представления функций. Он заключается в поиске корней системы уравнений и определении их точек пересечения.
Метод итераций:
Метод итераций является численным методом и предназначен для приближенного решения системы уравнений. Он заключается в последовательном приближении к точке пересечения графиков функций путем итерационного вычисления значений переменных.
Метод численного решения:
Этот метод основан на численных методах анализа функций и позволяет найти точки пересечения графиков функций с использованием численных методов интерполяции или приближенных вычислений.
При выборе метода определения пересечения графиков функций необходимо учитывать сложность функций, доступность вычислительных ресурсов и требования точности результата.
Аналитический метод нахождения пересечения графиков функций
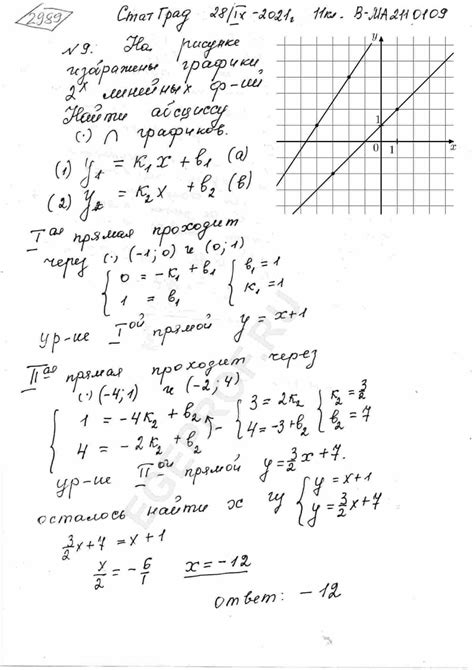
Для определения пересечения графиков функций существует аналитический метод, который позволяет точно найти координаты точек пересечения. Этот метод основывается на решении системы уравнений, где каждое уравнение соответствует одной из функций.
Предположим, у нас есть две функции f(x) и g(x), и мы хотим найти их точку пересечения. Для этого необходимо решить уравнение f(x) = g(x). Если фуnкции представлены в аналитической форме, то это может быть сделано путем алгебраических преобразований.
Например, пусть у нас есть функции f(x) = x^2 и g(x) = 2x + 1. Чтобы найти их точку пересечения, решим уравнение:
| Уравнение | Решение |
|---|---|
| x^2 = 2x + 1 | x^2 - 2x - 1 = 0 |
| Используя квадратное уравнение, найдем корни: | |
| x = (-b ± √(b^2 - 4ac)) / (2a) | x = (-(-2) ± √((-2)^2 - 4*1*(-1))) / (2*1) |
| Раскроем скобки и упростим выражение: | |
| x = (2 ± √(4 + 4)) / 2 | x = (2 ± √8) / 2 |
| x = (2 ± 2√2) / 2 | x = 1 ± √2 |
Таким образом, получили два решения для уравнения: x = 1 + √2 и x = 1 - √2. Именно эти значения x будут соответствовать точкам пересечения графиков функций f(x) и g(x).
В общем случае, аналитический метод нахождения пересечения графиков функций требует решения системы уравнений, что может занимать некоторое время. Однако, при использовании соответствующего программного обеспечения или математических пакетов, это можно сделать быстро и эффективно.
Графический метод определения пересечения графиков функций
Для определения пересечения графиков функций необходимо построить их графики на координатной плоскости. Затем необходимо проанализировать полученные графики и определить точки их пересечения.
Для построения графиков функций обычно используются графические программы или ручное построение с использованием таблицы значений функций. При построении графиков необходимо учесть диапазон значений переменных и особенности поведения функций в этом диапазоне.
После построения графиков функций можно определить точки их пересечения. Если графики пересекаются в одной точке, то это является решением уравнения или системы уравнений. Если графики не пересекаются, то уравнение или система уравнений не имеет решений.
Графический метод определения пересечения графиков функций является графическим интерпретатором математических уравнений и систем уравнений. Он позволяет визуально представить решения и провести анализ взаимодействия функций в заданном диапазоне значений переменных.
Численные методы для нахождения пересечения графиков функций
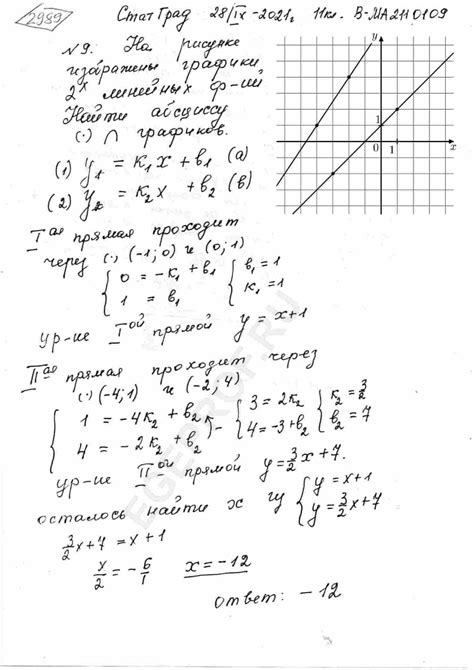
Установить точное аналитическое решение для пересечения графиков функций может быть сложной задачей, особенно для сложных и нелинейных функций. В таких случаях, численные методы могут предложить эффективное решение для нахождения пересечения графиков функций.
Один из наиболее распространенных численных методов для нахождения пересечения графиков функций - метод половинного деления (или метод бисекции). Этот метод основан на принципе непрерывности функции, итеративно уточняет интервал, в котором находится точка пересечения.
Для использования метода половинного деления, необходимо определить начальные значения интервала, в котором находится пересечение, и выбрать точность, с которой мы хотим найти пересечение. Затем, метод применяется итеративно, пока ширина интервала не станет достаточно мала.
Еще одним численным методом нахождения пересечения графиков функций является метод Ньютона-Рафсона. Этот метод основан на использовании касательной линии к графику функции в точке пересечения и локализует пересечение на основе негладкости функции.
Для применения метода Ньютона-Рафсона, необходимо выбрать начальное приближение для пересечения и условие остановки для уточнения точности. Метод находит новое приближение для пересечения, используя касательную линию в текущей точке, и повторяет этот процесс до достижения требуемой точности.
Однако, при использовании численных методов для нахождения пересечения графиков функций необходимо учитывать возможные ограничения и недостатки методов. Например, метод половинного деления может быть медленным для некоторых функций с большим количеством пересечений, а метод Ньютона-Рафсона может потребовать хорошего начального приближения для сходимости.
| Метод | Преимущества | Недостатки |
|---|---|---|
| Метод половинного деления | Прост в реализации Эффективный для функций с одним пересечением | Медленный для функций с множеством пересечений Требует начальных значений интервала |
| Метод Ньютона-Рафсона | Более быстрая сходимость Может использовать производные функции | Требует хороших начальных приближений Неустойчив к особенностям функции |
В зависимости от требований и условий задачи, различные численные методы могут быть применимы для нахождения пересечения графиков функций. Важно учитывать особенности функций, требования по скорости и точности, чтобы выбрать наиболее подходящий метод.



