Наша повседневная жизнь полна ситуаций, когда нам необходимо определить, принадлежит ли точка заданному графику на плоскости. Это может быть полезным при решении задач из различных областей, таких как геометрия, физика, экономика и многих других.
Определение принадлежности точки графику является одной из основных задач аналитической геометрии. Для решения этой задачи необходимо использовать знания о координатах точек на плоскости и уравнениях графиков различных функций.
Когда мы имеем уравнение графика или его графическое представление, определение принадлежности точки графику сводится к проверке, что значения координат этой точки удовлетворяют уравнению графика. Если это утверждение истинно, то точка принадлежит графику, иначе точка не принадлежит графику.
Однако в случае сложных графиков, уравнений или кривых, определение принадлежности точки может оказаться нетривиальным. Здесь на помощь приходят методы и алгоритмы вычислительной геометрии, которые позволяют определить принадлежность точки графику с высокой точностью.
Как определить, принадлежит ли точка графику?

Определение принадлежности точки графику на плоскости может быть полезным при решении различных задач, связанных с анализом графиков функций или построением графиков на основе заданных точек. В этом разделе мы рассмотрим несколько способов определить, принадлежит ли точка графику.
Один из способов состоит в том, чтобы вычислить значение функции в данной точке и сравнить его с координатами точки. Если значения совпадают, то точка принадлежит графику. Например, если дана функция f(x) = x^2 и точка (2, 4), то мы можем вычислить значение функции при x = 2 и проверить, равно ли оно 4. Если да, то точка (2, 4) принадлежит графику функции f(x) = x^2.
Другой способ заключается в построении графика функции и проверке, находится ли точка на этом графике. Для этого можно использовать координатную плоскость и нарисовать график функции или задать точки, через которые должен проходить график. Затем можно сравнить координаты данной точки с координатами точек, через которые проходит график. Если они совпадают, то точка принадлежит графику.
Также можно использовать методы математического анализа, например, дифференцирование функции и проверку, находится ли точка на графике в месте экстремума функции или её перегиба. Этот способ может быть более сложным, но иногда может дать более точный результат.
В завершение, важно отметить, что определение принадлежности точки графику может быть полезным при решении задач различной сложности. Умение определять, принадлежит ли точка графику, является важным навыком при работе с графиками функций и анализе данных на плоскости.
Определение точки на плоскости
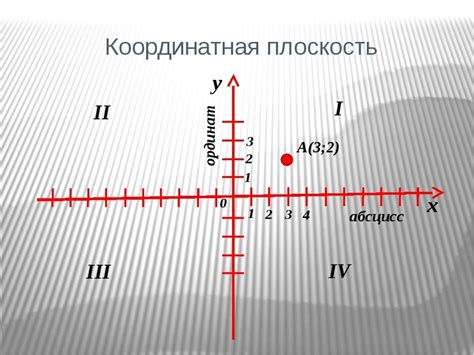
Существует несколько способов определить, принадлежит ли точка графику. Один из самых простых способов - это использование системы координат. На плоскости каждая точка имеет координаты, обозначенные парой чисел (x, y).
Если точка принадлежит графику, это означает, что ее координаты удовлетворяют уравнению, описывающему этот график. Например, если графиком является прямая, то точка принадлежит графику, если ее координаты удовлетворяют уравнению прямой.
Для более сложных графиков, таких как окружности, эллипсы или параболы, существуют специальные формулы, которые позволяют определить, принадлежит ли точка графику. Эти формулы основаны на свойствах геометрических фигур и могут быть использованы для проверки принадлежности точки графику.
Кроме того, существует также графический метод определения принадлежности точки графику. Для этого необходимо построить график на плоскости и визуально оценить положение точки относительно графика. Если точка находится на линии или плоскости графика, то она принадлежит графику.
Важно отметить, что точка может принадлежать только одному графику. Если точка находится на пересечении двух графиков, то она не принадлежит ни одному из них.
Метод графического решения
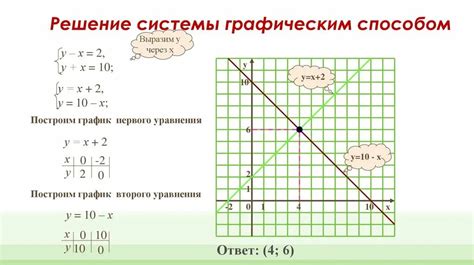
Для применения этого метода необходимо знать уравнение графика и координаты точки, которую нужно проверить.
Шаги метода графического решения:
- Найдите уравнение графика, если оно неизвестно. Запишите его в виде y = f(x), где y - выражение в зависимости от x.
- Постройте график этой функции на плоскости.
- Определите координаты точки, которую необходимо проверить.
- Проверьте, принадлежит ли эта точка графику. Для этого сравните координаты точки с уравнением графика: подставьте значение x точки в уравнение и проверьте, выполняется ли оно.
- Если значение y, полученное при подстановке, совпадает с y-координатой точки, то точка принадлежит графику. В противном случае точка не принадлежит графику.
Метод графического решения позволяет быстро и наглядно определить, принадлежит ли точка графику. Однако он имеет ограничения и не всегда является точным. Для более точного определения рекомендуется использовать другие методы, такие как аналитическое решение или численные методы.
Проверка координат
Для проверки координат нужно знать уравнение графика или его характерные особенности.
Если уравнение графика дано в явной форме, то для проверки координат подставляем значения x в это уравнение и сравниваем полученный y с координатой y заданной точки. Если значения совпадают, то точка принадлежит графику.
Если уравнение графика дано в параметрической форме, нужно подставить заданные значения в x и y и сравнить их с соответствующими координатами точки.
Также существует способ проверки координат для специфических графиков, таких, как окружность или прямоугольник. В этих случаях нужно задать допустимые значения для x и y и сравнить их с координатами точки.
Важно помнить, что проверка координат является лишь одним из методов определения принадлежности точки графику. Для более точного результата рекомендуется использовать и другие методы, в зависимости от типа графика и доступных данных.
Теорема Пифагора в графике
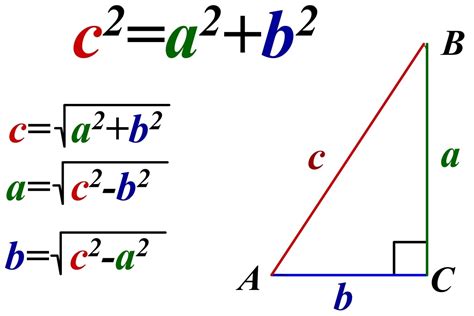
Теорема Пифагора, известная в математике, также может быть применена для определения принадлежности точки графику на плоскости. Эта теорема устанавливает связь между длинами сторон прямоугольного треугольника.
В графике на плоскости можно представить треугольник с вершинами в точках (x1, y1), (x2, y2) и (x3, y3). Для определения, принадлежит ли точка (x, y) графику этого треугольника, можно использовать теорему Пифагора.
Для этого необходимо:
- Вычислить длины сторон треугольника:
- Вычислить длины отрезков от вершин треугольника до точки (x, y):
- Сравнить сумму длин отрезков от вершин треугольника до точки (x, y) с суммой длин сторон треугольника:
| Сторона | Длина |
| AB | √((x2 - x1)2 + (y2 - y1)2) |
| BC | √((x3 - x2)2 + (y3 - y2)2) |
| AC | √((x3 - x1)2 + (y3 - y1)2) |
| Отрезок | Длина |
| AD | √((x - x1)2 + (y - y1)2) |
| BD | √((x - x2)2 + (y - y2)2) |
| CD | √((x - x3)2 + (y - y3)2) |
- Если сумма длин отрезков равна сумме длин сторон, то точка (x, y) принадлежит графику треугольника.
- Если сумма длин отрезков больше суммы длин сторон, то точка (x, y) лежит вне графика треугольника.
- Если сумма длин отрезков меньше суммы длин сторон, то точка (x, y) лежит внутри графика треугольника.



