Параллелограмм – это особый вид четырехугольника, у которого противоположные стороны параллельны. В геометрии этой фигуры значительное значение имеет его высота. Она помогает нам измерить расстояние между основаниями параллелограмма и определить его площадь. В этой статье мы рассмотрим, как найти высоту параллелограмма по сторонам.
Формула для вычисления высоты параллелограмма по его сторонам достаточно проста. Для этого необходимо знать длину одной из его сторон и расстояние между ней и противоположной стороной, которое мы и называем высотой. Высота параллелограмма обозначается символом h. Формула может быть записана следующим образом: h = S/a, где S – площадь параллелограмма, а a – длина основания.
Рассмотрим пример вычисления высоты параллелограмма по сторонам. Предположим, что длина одного из оснований параллелограмма равна 8 см, а расстояние между ним и противоположной стороной – 5 см. Площадь параллелограмма составляет 40 квадратных сантиметров. Подставляя все значения в формулу, получаем: h = 40/8 = 5 см. Таким образом, высота параллелограмма равна 5 см.
Что такое параллелограмм и его стороны
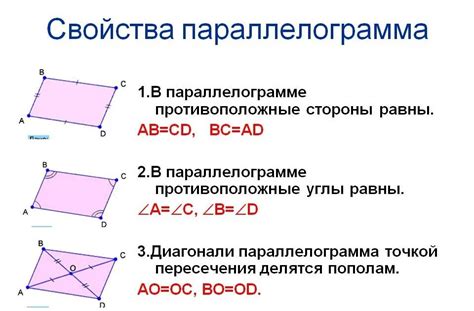
У параллелограмма есть три основных типа сторон:
- Стороны: это отрезки, соединяющие вершины параллелограмма. Он имеет обычно четыре стороны, обозначаемые как a, b, c и d.
- Основания: это парные параллельные стороны параллелограмма. Они обычно обозначаются как a и c. Основания определяют ширину параллелограмма.
- Высота: это перпендикуляр, опущенный из основания параллелограмма на противоположное основание или продолжение противоположного основания. Он обозначается как h и определяет вертикальное расстояние между основаниями параллелограмма.
Знание всех этих характеристик позволяет нам рассчитать высоту параллелограмма по заданным сторонам, что может быть полезно при решении различных геометрических задач и построении фигур.
Как найти высоту параллелограмма по сторонам: общая формула

Для определения высоты параллелограмма по заданным сторонам необходимо использовать общую формулу. Обозначим стороны параллелограмма как a и b, а высоту как h.
Общая формула для нахождения высоты параллелограмма по сторонам выглядит следующим образом:
| h | = | 2 * (Площадь параллелограмма) |
| a |
Таким образом, чтобы найти высоту параллелограмма, нужно вычислить его площадь и разделить на длину одной из сторон.
Пример:
Пусть дан параллелограмм со сторонами a = 6 и b = 8. Найдем высоту h.
Для начала, нужно найти площадь параллелограмма. Площадь параллелограмма равна произведению длины одной из сторон на высоту, т.е.
Площадь = a * h
Так как нам известны стороны параллелограмма, мы можем использовать формулу для нахождения площади:
Площадь = a * b
Подставляем данные в формулу:
Площадь = 6 * 8 = 48
Теперь, используя общую формулу, найдем высоту:
h = 2 * Площадь / a = 2 * 48 / 6 = 16
Таким образом, высота заданного параллелограмма равна 16.
Пример вычисления высоты по сторонам
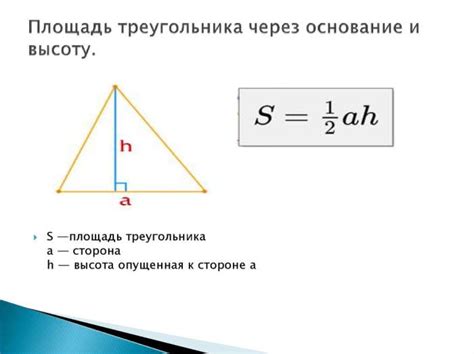
Для вычисления высоты параллелограмма по сторонам необходимо знать длины этих сторон. Рассмотрим пример:
Пусть у нас есть параллелограмм ABCD, в котором известны следующие стороны:
- AB = 8 см
- BC = 6 см
Чтобы найти высоту, мы можем использовать формулу:
Высота = площадь / основание
где площадь равна произведению длины одной стороны на высоту, а основание - любая из сторон параллелограмма.
В нашем примере, возьмем сторону AB в качестве основания. Длина основания равна 8 см. Следовательно, чтобы найти высоту, нам необходимо узнать площадь параллелограмма. Площадь параллелограмма равна произведению длин сторон, перпендикулярных друг другу. В данном случае, длины этих сторон равны AB и AD.
AD - это высота параллелограмма. Поэтому, чтобы найти высоту, мы должны разделить площадь параллелограмма на основание:
Высота = AB * AD / AB = AD
Известно, что площадь параллелограмма равна 8 см * AD. Подставим это значение в формулу для высоты:
AD = 8 см * AD / 8 см = AD
Таким образом, высота параллелограмма равна AD, то есть, 6 см.
В данном примере мы использовали формулу для вычисления высоты параллелограмма по сторонам и нашли высоту равной 6 см. Этот пример демонстрирует применение формулы и позволяет понять, как вычислять высоту в аналогичных случаях.
Использование теоремы Пифагора для нахождения высоты

Высоту параллелограмма можно найти, используя теорему Пифагора. Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин двух катетов. В случае параллелограмма, квадрат длины высоты равен сумме квадратов длин двух сторон, перпендикулярных этой высоте.
Пусть a и b - стороны параллелограмма, c - его высота. Тогда можно записать следующее равенство:
a^2 = b^2 + c^2
Используя это равенство, можно решить уравнение относительно высоты c:
c^2 = a^2 - b^2
Высоту параллелограмма можно найти, извлекая квадратный корень из найденного значения:
c = √(a^2 - b^2)
Например, если сторона a равна 6, а сторона b равна 4, то можно найти высоту c:
с = √(6^2 - 4^2) = √(36 - 16) = √20 ≈ 4.47
Таким образом, высота параллелограмма с данными сторонами равна примерно 4.47.
Вычисление высоты параллелограмма по сторонам: практические советы

Пусть a и b – это длины оснований параллелограмма, а h – его высота. Тогда формула для вычисления высоты параллелограмма будет выглядеть следующим образом:
h = 2 * S / a
где S – площадь параллелограмма.
Для примера, пусть у нас есть параллелограмм со сторонами a = 6 и b = 10. Чтобы найти его высоту, мы сначала должны найти площадь, используя формулу S = a * h. Если площадь равна 24, высота параллелограмма будет:
h = 2 * 24 / 6 = 8
Таким образом, высота параллелограмма будет равна 8.
Зная формулу и применяя практические советы, вы сможете легко вычислить высоту параллелограмма по его сторонам. Это позволит вам более точно определить его геометрические характеристики и использовать в практических расчетах.
Примеры вычисления высоты параллелограмма

Для нахождения высоты параллелограмма по сторонам необходимо использовать формулу:
h = A / b
Где:
- h - высота параллелограмма
- A - площадь параллелограмма
- b - длина основания параллелограмма
Рассмотрим примеры:
Пример 1:
Пусть площадь параллелограмма равна 20 квадратных сантиметров, а длина основания равна 5 сантиметров.
Используя формулу, вычислим высоту:
h = 20 / 5 = 4 сантиметра
Таким образом, высота параллелограмма равна 4 сантиметра.
Пример 2:
Пусть площадь параллелограмма равна 36 квадратных метров, а длина основания равна 6 метров.
Используя формулу, вычислим высоту:
h = 36 / 6 = 6 метров
Таким образом, высота параллелограмма равна 6 метров.
И так далее, вы можете использовать данную формулу для вычисления высоты параллелограмма по его сторонам в любом другом примере.



