Решение задач, связанных с дробными числами, является важным навыком в математике. Особенно важно научиться правильно работать с дробями, у которых знаменатель неизвестен или отличается от 1. Чтобы успешно решать такие задачи, необходимо овладеть несколькими основными принципами и приемами.
Первый принцип: при домножении дроби на некоторое число, знаменатель не меняется, а числитель умножается на это число. Это позволяет привести дробь к нужному виду и упростить решение задачи. Например, если у нас имеется дробь с знаменателем 5, и мы умножаем числитель и знаменатель на 3, то получим новую дробь с знаменателем 15.
Второй принцип: для сложения или вычитания дробей с разными знаменателями, необходимо привести их к общему знаменателю. Для этого следует найти наименьшее общее кратное знаменателей и умножить каждую дробь на такое число, чтобы ее знаменатель стал равным общему знаменателю. Затем уже можно складывать или вычитать числители дробей.
Таким образом, правильное решение дробей с знаменателем требует умения приводить их к нужному виду и оперировать числителями и знаменателями. Владение этими основными принципами и советами поможет справляться с задачами, связанными с дробными числами, и успешно выполнять задания в математике.
Основные принципы решения дробей с знаменателем

Решение дробей с знаменателем может быть выполнено с использованием нескольких основных принципов. Эти принципы помогут упростить процесс решения и повысить точность получаемых результатов.
- Нахождение общего знаменателя. Для того чтобы сложить или вычесть дроби, их знаменатели должны быть одинаковыми. В случае разных знаменателей необходимо найти их общий знаменатель путем поиска наименьшего общего кратного. После нахождения общего знаменателя дроби можно привести к общему знаменателю и выполнить операции.
- Приведение дроби к несократимому виду. Для удобства решения дробей и получения более простого ответа, рекомендуется привести дроби к несократимому виду. Для этого необходимо найти их наибольший общий делитель и поделить числитель и знаменатель на этот делитель.
- Выполнение арифметических операций. После приведения дробей к общему знаменателю и приведения к несократимому виду можно выполнять арифметические операции над дробями. Для сложения или вычитания дробей, сложите или вычтите их числители и сохраните общий знаменатель. Для умножения, перемножьте числители и знаменатели. Для деления, умножьте первую дробь на обратную второй.
- Проверка и упрощение ответа. После выполнения арифметических операций рекомендуется проверить ответ и упростить его, если это возможно. Если полученная дробь может быть сокращена, найдите их наибольший общий делитель и поделите числитель и знаменатель на этот делитель.
Соблюдение этих принципов поможет вам решать дроби с знаменателем более эффективно и получать более точные результаты. Практика и умение применять эти принципы в различных ситуациях помогут вам развить навыки решения дробей и использовать их в реальных задачах.
Что такое дробь с знаменателем
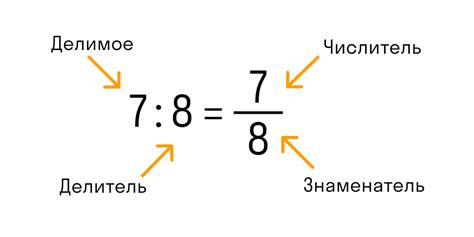
Знаменатель в дроби определяет количество равных частей, на которые число разделено. Например, в дроби 3/4 знаменатель равен 4, что означает, что единица разделена на 4 равные части, и в числителе находится 3 из них.
Дробь с знаменателем может быть положительной или отрицательной, в зависимости от знака числителя. Если числитель положительный, то и дробь считается положительной, если числитель отрицательный, то и дробь считается отрицательной.
Дроби с знаменателем широко используются в математике и в различных практических ситуациях, таких как деление предмета на равные части, измерение углов и многое другое. Понимание основных принципов решения дробей с знаменателем позволяет успешно работать с ними и использовать в решении математических задач.
| Примеры дробей с знаменателем | Пояснение |
|---|---|
| 1/2 | Один равный кусок из двух равных частей |
| 3/4 | Три равных куска из четырех равных частей |
| -5/7 | Пять равных кусков из семи равных частей, со знаком минус перед числителем |
Какие принципы применяются при решении дробей с знаменателем

Решение дробей с знаменателем требует соблюдения определенных принципов, чтобы выполнить задачу корректно и получить точный результат. Вот основные принципы, которые следует учитывать:
- Перевод дроби в общий знаменатель: Если в задаче требуется сложение или вычитание дробей с разными знаменателями, необходимо привести дроби к общему знаменателю. Для этого найдите наименьшее общее кратное (НОК) знаменателей и умножьте каждую дробь на необходимый множитель.
- Упрощение дробей: После перевода дробей в общий знаменатель, можно упростить полученные дроби, если это возможно. Для этого найдите общий делитель числителя и знаменателя и поделите их на него, чтобы получить максимально сокращенную дробь.
- Выполнение операций: После приведения дробей к общему знаменателю и их упрощения, можно выполнять нужные операции (сложение, вычитание, умножение или деление). Следите за сохранением правильного знака и правильного порядка операций.
- Замена смешанных чисел: Если в задаче присутствуют смешанные числа, то их необходимо заменить неправильными дробями. Для этого умножьте целую часть на знаменатель и прибавьте числитель. Полученное значение станет новым числителем, а старый знаменатель сохранится. Затем продолжайте решать задачу как обычно.
- Проверка результата: В конце решения задачи с дробями сделайте проверку результата. Для этого выполните обратную операцию или используйте простые арифметические действия, чтобы убедиться, что полученный ответ верный.
Соблюдение данных принципов поможет вам эффективно решать задачи с дробями с знаменателем и получать правильные ответы. Помните, что практика и постоянное применение этих принципов помогут вам стать лучше в решении подобных задач.
Ключевые советы по решению дробей с знаменателем

Решение дробей с знаменателем может быть для некоторых людей сложным и запутанным процессом. Однако, с помощью нескольких ключевых советов и принципов, вы сможете упростить эту задачу и успешно решить дроби с знаменателем.
- 1. Внимательно прочитайте задачу. Понимание условия и требований задачи является первым и самым важным шагом при решении дробей с знаменателем.
- 2. Приведите знаменатель к общему знаменателю. Это позволит вам складывать и вычитать дроби с разными знаменателями. Для этого найдите наименьшее общее кратное знаменателей и приведите каждую дробь к этому знаменателю.
- 3. Упростите дроби. Если знаменатель и числитель имеют общие делители, упростите дробь, разделив их на наибольший общий делитель. Это позволит вам работать с более простыми числами и упростит последующие вычисления.
- 4. Складывайте или вычитайте числители. Если знаменатели у вас уже приведены к общему знаменателю, просто складывайте или вычитайте числители дробей. Результат будет новым числителем результирующей дроби.
- 5. Приведите результат к наименьшей общей дроби. Если возможно, упростите вновь полученную дробь, разделив числитель и знаменатель на наибольший общий делитель. Таким образом, вы получите окончательное решение дроби с знаменателем в наименьшем виде.
Следуя этим ключевым советам, вы сможете решать дроби с знаменателем без проблем и достигнуть правильного результата. Практика и дальнейшее изучение этой темы помогут вам в дальнейшем развитии навыков решения дробей.
Примеры решения дробей с знаменателем

Давайте рассмотрим несколько примеров решения дробных чисел с знаменателем. Эти примеры помогут вам лучше понять основные принципы и подходы к работе с дробями.
Пример 1:
Решим дробь 3/5.
Для этого нужно разделить числитель на знаменатель: 3 ÷ 5 = 0,6.
Таким образом, дробь 3/5 равна 0,6.
Пример 2:
Решим дробь 7/8.
Для этого нужно разделить числитель на знаменатель: 7 ÷ 8 = 0,875.
Таким образом, дробь 7/8 равна 0,875.
Пример 3:
Решим дробь 10/3.
Для этого нужно разделить числитель на знаменатель: 10 ÷ 3 ≈ 3,33 (округляем до второго знака после запятой).
Таким образом, дробь 10/3 примерно равна 3,33.
В каждом примере мы разделили числитель на знаменатель, чтобы получить десятичное значение дроби. Во втором и третьем примерах результат имеет несколько знаков после запятой.
Вы можете использовать эти примеры как руководство при решении дробей с знаменателем. Помните, что десятичные значения могут быть точными или приближенными, в зависимости от длины десятичной дроби.
Практическая польза решения дробей с знаменателем

Решение дробей с знаменателем имеет множество практических применений и подходит для решения широкого спектра задач в различных областях. Вот несколько сфер, где знание и понимание этой темы может быть полезным:
Финансы и бухгалтерия:
Решение дробных уравнений и вычисление долей частей позволяют эффективно управлять финансовыми ресурсами, распределять доходы и расходы на основе определенных пропорций и соотношений. Так, например, при расчете долей акционеров или при дележе прибылей и убытков между участниками компании необходимо использовать решение дробей.
Инженерия и строительство:
Решение дробей широко применяется в инженерном и строительном деле для вычисления материальных объемов при проектировании и строительстве зданий, мостов, дорог и других сооружений. Дроби позволяют точно определить необходимое количество материалов и ресурсов на каждом этапе процесса, что в свою очередь влияет на экономию времени и средств.
Медицина и фармакология:
Расчеты доз лекарственных препаратов, пропорций компонентов в рецептуре и решение других задач в области медицины требуют знания дробных выражений. Благодаря решению дробей можно точно определить требуемые пропорции и дозировки, что позволяет достичь максимальной эффективности в лечении и минимизировать побочные эффекты.
Статистика и эконометрика:
Умение решать дробные выражения и работать с знаменателями является важным навыком, который может быть полезным в различных сферах жизни и профессиональной деятельности. Освоив эту тему и понимание ее применения, вы сможете эффективно решать задачи, улучшать процессы и повышать свою профессиональную компетенцию.



