Определение вхождения числа в заданный промежуток является важной задачей в математике, программировании и других областях. Это позволяет нам проверить, принадлежит ли данное число определенному диапазону значений и выполнить определенные действия на основе этого результата.
Для определения вхождения числа в заданный промежуток, необходимо учитывать исходные данные и условия задачи. Если нам известны начальное и конечное значения промежутка, а также число, которое мы хотим проверить, мы можем использовать математические операции и логические выражения для определения результата.
Преимущество определения вхождения числа в заданный промежуток заключается в возможности создания универсальных алгоритмов и программ, которые могут работать с различными наборами данных. Это пригодится нам при разработке игр, программировании роботов, анализе данных и других сферах деятельности.
В данной статье мы рассмотрим несколько способов определения вхождения числа в заданный промежуток, включая использование условных операторов, математических функций и стандартных методов программирования. Также мы рассмотрим примеры кода на разных языках программирования, которые помогут нам лучше понять данную тему и применить полученные знания в практических задачах.
Как определить вхождение числа в промежуток

Для начала, необходимо определить, какой промежуток чисел мы будем рассматривать. Для этого используются два числа - начало и конец промежутка. Например, если мы хотим определить, входит ли число в промежуток от 1 до 10, то начало будет равно 1, а конец - 10.
В случае если число входит в заданный промежуток, условное выражение должно возвращать значение "Истина". Для проверки этого условия используется оператор сравнения (<, >, <=, >=) с помощью логического оператора "и".
Например, чтобы проверить, входит ли число 5 в промежуток от 1 до 10, можно использовать следующие выражение:
если (число >= начало) и (число <= конец) то
В текущем примере, условное выражение вернет значение "Истина", так как число 5 входит в заданный промежуток от 1 до 10.
Если же число не входит в заданный промежуток, то условное выражение вернет значение "Ложь". В этом случае можно использовать оператор "или" для проверки нескольких промежутков одновременно.
Например, для определения, входит ли число 15 в промежуток от 1 до 10 или от 20 до 30, можно использовать следующее выражение:
если (число >= начало1) и (число <= конец1) или (число >= начало2) и (число <= конец2) то
В данном случае, условное выражение вернет значение "Ложь", так как число 15 не входит ни в один из заданных промежутков.
Таким образом, определение вхождения числа в заданный промежуток является важной задачей в программировании и может быть решена с помощью условных операторов и логических выражений.
Число и его промежуток
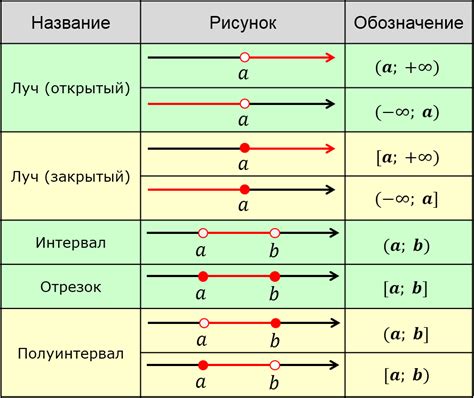
Промежуток может быть задан двумя числами - началом и концом, или быть бесконечным. Если промежуток является закрытым, то это означает, что числа в нем могут быть равны началу или концу промежутка. Если промежуток является открытым, то числа в нем не могут достигать начала или конца.
Для определения вхождения числа в промежуток можно использовать условный оператор. Если число больше начала и меньше конца, или равно граничным значениям в случае закрытого промежутка, то оно находится внутри промежутка. В противном случае, число не входит в указанный диапазон.
Для более наглядного представления информации о числе и его промежутке, можно использовать таблицу. В таблице можно указать числовой промежуток, а также входящие в него числа, чтобы информация была более очевидной и понятной.
| Промежуток | Числа |
|---|---|
| [3, 8] | 3, 4, 5, 6, 7, 8 |
| (-∞, 0) | любое число меньше 0 |
| [10, ∞) | любое число больше или равное 10 |
Таким образом, для определения вхождения числа в заданный промежуток необходимо проверить его значение относительно начала и конца промежутка, а также учесть вид промежутка (закрытый или открытый).
Определение вхождения числа

Для решения этой задачи можно использовать различные подходы. Одним из наиболее распространенных способов является сравнение числа с минимальным и максимальным значениями заданного промежутка.
В следующей таблице приведены шаги для определения вхождения числа:
| Шаг | Описание |
|---|---|
| 1 | Задать минимальное и максимальное значения промежутка |
| 2 | Проверить, является ли число меньше или равным максимальному значению и больше или равным минимальному значению |
| 3 | Если условие из шага 2 истинно, то число принадлежит заданному промежутку, иначе - не принадлежит |
Например, чтобы определить, принадлежит ли число 5 промежутку от 1 до 10, нужно проверить, что оно больше или равно 1 и меньше или равно 10. Если это условие выполняется, то число 5 принадлежит указанному промежутку.
Знание алгоритма определения вхождения числа позволяет эффективно работать с промежутками чисел в программировании и решать различные задачи, связанные с манипуляцией числами и их анализом.
Примеры определения вхождения чисел

Вхождение числа в заданный промежуток можно определить с помощью условных операторов и математических операций. Рассмотрим несколько примеров:
1. Пусть дано число x = 5. Чтобы узнать, входит ли оно в промежуток от 1 до 10 (включительно), можно использовать следующее условие:
if x >= 1 and x <= 10:
print("Число входит в промежуток")
else:
print("Число не входит в промежуток")
2. Если необходимо определить вхождение числа в промежуток с помощью функции, можно использовать следующий код:
def is_in_range(num):
if num >= 20 and num <= 30:
return True
else:
return False
print(is_in_range(25)) # Выведет True
print(is_in_range(40)) # Выведет False
3. В зависимости от задачи, можно использовать разные математические операции для определения вхождения числа в промежуток. Например:
def is_even(num):
if num % 2 == 0:
return True
else:
return False
print(is_even(4)) # Выведет True
print(is_even(7)) # Выведет False
Это лишь несколько примеров того, как можно определить вхождение числа в заданный промежуток. В каждом конкретном случае необходимо выбирать подходящий подход и условия, основываясь на требованиях задачи.



