Прямоугольник - это одна из самых распространенных геометрических фигур, которую мы встречаем в нашей жизни повсюду. Иногда, нам может понадобиться вычислить размеры его сторон, зная только его площадь. Как это сделать?
Для начала, нам следует напомнить, что площадь прямоугольника вычисляется как произведение длин его сторон. Если мы знаем площадь прямоугольника, но не знаем его стороны, мы можем использовать алгоритм для нахождения размеров сторон.
Чтобы найти размеры сторон прямоугольника при заданной площади, мы можем использовать математическую формулу: сторона прямоугольника равна квадратному корню из его площади, деленной на противоположную сторону.
Способы вычисления размеров прямоугольника при известной площади

Существует несколько способов вычисления размеров сторон прямоугольника при известной площади:
1. Использование формулы
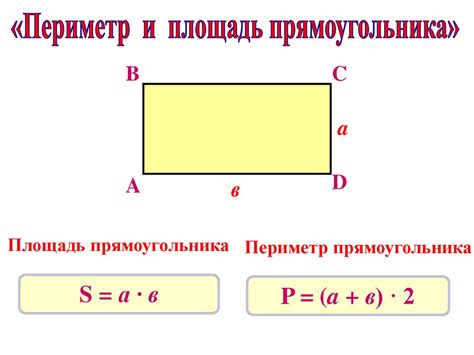
Площадь прямоугольника можно вычислить, зная длину одной из сторон и площадь фигуры. Формула для вычисления площади прямоугольника: S = a * b, где S - площадь, a - длина одной стороны, b - длина другой стороны. Если известна площадь и одна из сторон, можно выразить вторую сторону через известные значения.
2. Решение квадратного уравнения
Площадь прямоугольника можно рассматривать как площадь квадрата со стороной x, где x - неизвестное значение. Подставив площадь прямоугольника в формулу квадрата (S = x^2), можно решить квадратное уравнение и найти значение стороны x, а затем вычислить длины сторон прямоугольника.
3. Использование геометрической формулы
Для прямоугольника с площадью S существует формула для вычисления сторон: a = sqrt(S / k), b = sqrt(S * k), где a и b - длины сторон прямоугольника, k - произвольное число, влияющее на форму прямоугольника и его соотношение сторон. Выбор значения k позволяет варьировать форму прямоугольника.
Используя эти способы, можно легко вычислить размеры сторон прямоугольника при известной площади и получить необходимые данные для построения или расчетов. Имейте в виду, что размеры сторон прямоугольника могут быть представлены в различных единицах измерения (сантиметры, метры и т. д.), поэтому при решении задачи необходимо учитывать выбранную единицу измерения.
Формула нахождения сторон прямоугольника

Для нахождения размеров сторон прямоугольника при известной площади необходимо использовать следующую формулу:
Площадь прямоугольника = длина * ширина
Где:
- Площадь прямоугольника - это значение, известное заранее
- Длина - одна из сторон прямоугольника (неизвестное значение)
- Ширина - другая сторона прямоугольника (также неизвестное значение)
Используя данную формулу, можно определить значения длины и ширины прямоугольника, зная его площадь. Это может быть полезно, например, при решении задач из геометрии или в строительстве.
Метод решения квадратного уравнения

Для решения квадратного уравнения существует специальная формула, называемая формулой дискриминанта. Дискриминант - это выражение, вычисляемое по следующей формуле:
D = b^2 - 4ac.
Зная значение дискриминанта, можно определить, какого типа будет решение квадратного уравнения:
- Если D > 0, то уравнение имеет два различных вещественных корня;
- Если D = 0, то уравнение имеет один вещественный корень - это так называемый уравнение с "двойным корнем";
- Если D < 0, то уравнение не имеет вещественных корней, но имеет два комплексных корня.
Решение квадратного уравнения можно найти при помощи формулы:
x = (-b ± √D) / (2a).
Здесь ± означает, что нужно рассмотреть два варианта решения: с плюсом и с минусом. Если D = 0, то используется только одно решение.
Геометрическое построение для определения сторон прямоугольника

Если известна площадь прямоугольника, то его стороны можно вычислить с помощью геометрического построения. Для этого необходимо выполнить следующие шаги:
- Найти квадратный корень из заданной площади. Это будет длина одной из сторон прямоугольника.
- Найти отношение площади прямоугольника к известной стороне. Например, если известна площадь и ширина прямоугольника, то отношение будет равно площади деленной на ширину.
- Найти вторую сторону прямоугольника путем деления площади на длину одной из сторон.
Эти шаги позволяют определить размеры сторон прямоугольника при известной площади.
| Шаг | Описание |
|---|---|
| 1 | Известна площадь прямоугольника: S |
| Находим длину одной из сторон: a = √S | |
| 2 | Известна площадь и одна из сторон: S, a |
| Находим отношение площади к известной стороне: Отношение = S / a | |
| 3 | Известна площадь и одна из сторон: S, a |
| Находим вторую сторону прямоугольника: Вторая сторона = S / a |
Правила расчета сторон прямоугольника на примере задач

Расчет размеров сторон прямоугольника может быть важным при выполнении различных задач. Например, при проектировании строительных объектов или создании дизайна интерьера. Существует несколько способов определения сторон прямоугольника на основе его площади.
Один из самых простых способов - найти два числа, произведение которых равно данной площади. Эти числа будут являться значениями сторон прямоугольника. Допустим, мы имеем прямоугольник площадью 24 квадратных метра. Можно привести несколько примеров пар чисел, произведение которых равно 24: (2, 12), (3, 8), (4, 6). Это означает, что возможны следующие комбинации сторон: 2 м и 12 м, 3 м и 8 м, 4 м и 6 м.
Также для расчета размеров сторон прямоугольника можно использовать формулу, основанную на решении квадратного уравнения. Если известна площадь S и одна из сторон x, то вторую сторону можно найти, поделив площадь на известную сторону: S / x = y, где y - вторая сторона. Например, если площадь прямоугольника составляет 36 квадратных метров, а одна из его сторон равна 6 метрам, то вторая сторона можно вычислить следующим образом: 36 / 6 = 6 метров.
| Площадь (S) | Известная сторона (x) | Результат |
|---|---|---|
| 30 квадратных метров | 5 метров | 6 метров |
| 48 квадратных метров | 8 метров | 6 метров |
| 64 квадратных метра | 8 метров | 8 метров |
Используя эти простые правила расчета, можно быстро и точно определить размеры сторон прямоугольника на основе его площади. При этом важно учитывать, что стороны прямоугольника должны быть положительными числами, иначе они будут лишь представлять абстрактные значения, не имеющие физического смысла.
Математический анализ для нахождения сторон прямоугольника

Пусть х и у - это длины сторон прямоугольника, а S - его площадь. Используя формулу площади прямоугольника S = х * у, мы можем найти одну сторону прямоугольника, исходя из известной площади и длины другой стороны. Для этого необходимо разделить площадь на длину известной стороны: х = S / у или у = S / х.
Таким образом, находясь у нас есть площадь прямоугольника и известна длина одной из его сторон, мы можем легко вычислить длину другой стороны с помощью математического анализа.
Не забывайте, что при нахождении размеров сторон прямоугольника следует использовать только положительные значения, так как длины сторон не могут быть отрицательными.
Программный способ определения размеров прямоугольника
Для вычисления размеров сторон прямоугольника при данной площади можно использовать следующий алгоритм:
- Вводим значение площади прямоугольника, которое мы знаем.
- Используя математическую формулу, находим одну сторону прямоугольника, разделив площадь на известную сторону.
- Затем, используя найденное значение, вычисляем вторую сторону прямоугольника, разделив площадь на найденную сторону.
- В результате получаем две стороны прямоугольника при заданной площади.
Программно задачу можно решить на языках программирования, таких как Python, Java или JavaScript, используя простые математические операции и переменные. В коде программы можно добавить проверку на ввод корректных данных и обработку ошибок.
Задачи и упражнения по вычислению сторон прямоугольника
- Задача 1: Найдите размеры прямоугольника с площадью 24 квадратных единиц, если одна сторона равна 4 единицам. Какой будет вторая сторона?
- Задача 2: Известно, что прямоугольник имеет площадь 40 квадратных метров. Одна из его сторон составляет 8 метров. Чему равна вторая сторона?
- Задача 3: Найдите размеры прямоугольника, если его площадь равна 63 квадратным сантиметрам, а одна из его сторон равна 9 сантиметров.
- Задача 4: Площадь прямоугольника составляет 72 квадратные единицы. Одна из его сторон равна 8 единицам. Определите вторую сторону прямоугольника.
Решение каждой задачи требует использования формулы для площади прямоугольника: S = a * b, где S - площадь, a - длина одной стороны, b - длина второй стороны.
Для решения каждой задачи можно использовать следующий подход:
- Вывести на экран известные данные (площадь и длина одной из сторон).
- Используя формулу для площади прямоугольника, вычислить значение второй стороны.
- Вывести результат на экран.
Не забывайте проверять свои ответы, используя другие методы и инструменты, чтобы удостовериться в их точности.
- Если изначально известны только площадь прямоугольника и одна из его сторон, можно использовать формулу, основанную на свойствах прямоугольника. Например, для вычисления другой стороны можно разделить площадь на известную сторону.
- Использование геометрических методов, таких как разложение площади на меньшие прямоугольники или квадраты, может помочь при вычислении размеров сторон прямоугольника. Например, если площадь прямоугольника равна 24 квадратным сантиметрам, а известна одна из его сторон, можно разложить площадь на 6 меньших прямоугольников с площадью по 4 квадратных сантиметра и вычислить размеры сторон каждого меньшего прямоугольника.
- Методика использования формулы для нахождения сторон прямоугольника, основанной на квадратном корне из площади, может быть более универсальной, так как позволяет вычислить размеры обеих сторон прямоугольника. Однако, необходимо быть внимательными при применении такой формулы, чтобы избежать ошибок в вычислениях.
- При использовании методики нахождения размеров сторон прямоугольника на основе его диагонали и площади, важно помнить, что эта методика применима только в случае, когда известна площадь и диагональ прямоугольника.
Рекомендуется использовать различные методики вычисления размеров сторон прямоугольника в зависимости от доступной информации. Если изначально известна только площадь и одна из сторон, то можно воспользоваться простыми формулами, основанными на свойствах прямоугольника. Если же есть дополнительные данные, например, диагональ или возможность разложения площади на меньшие прямоугольники, то стоит использовать соответствующие методики для достижения более точных результатов.



