Касательная к графику – это прямая линия, которая касается графика функции и имеет один общий точку с ней. При этом касательная линия является параллельной оси абсцисс. Касательные часто используются в математике и физике для решения различных задач, а также в графическом представлении функций и кривых.
Касательная к графику имеет несколько основных свойств. Во-первых, она имеет один общий точку с графиком функции, что означает, что в этой точке значения функции и касательной совпадают. Во-вторых, касательная линия является прямой, а ее угол наклона равен наклону касаемой кривой в данной точке. В-третьих, касательная параллельна оси абсцисс, то есть все точки касательной имеют один и тот же y-координату.
Касательные имеют широкое применение в различных областях знаний. Например, они используются в теории вероятностей и статистике для аппроксимации функций и оценки их поведения вблизи определенной точки. Кроме того, касательные линии позволяют определить поведение функции вблизи экстремума, когда график меняет свое направление. В физике касательные применяются для описания движения тел и определения их скорости и ускорения в заданный момент времени.
Определение и геометрическое представление
Геометрическое представление касательной к графику, параллельной оси абсцисс, можно получить с использованием метода проекций. Для этого необходимо выбрать точку на графике функции, провести горизонтальную прямую линию через эту точку и приложить ее к оси абсцисс. Таким образом, получится касательная, параллельная оси абсцисс.
Касательная к графику, параллельная оси абсцисс, позволяет определить наклон графика в данной точке. Если график наклонен вверх, то касательная будет иметь положительный наклон, если график наклонен вниз, то наклон касательной будет отрицательным. Наклон касательной также дает информацию о скорости изменения функции в данной точке и особенно важен при изучении производной функции.
Уравнение касательной к графику
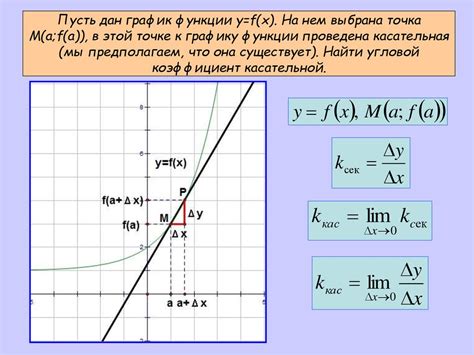
Для нахождения уравнения касательной к графику в определенной точке необходимо знать координаты этой точки и наклон графика в данной точке. Наклон графика можно найти при помощи производной функции в данной точке.
Уравнение касательной можно записать в общем виде:
- Для функции y = f(x) сначала находим производную f'(x).
- Затем находим значение производной в данной точке (например, f'(a), где a – координата точки).
- Используя полученную производную и координаты точки, можем записать уравнение касательной в виде y - f(a) = f'(a)(x - a).
Таким образом, уравнение касательной к графику позволяет определить точное положение этой линии на плоскости. Это может быть полезно для нахождения точных значений функции или изучения поведения функции в данной точке.
Точка касания и угловой коэффициент
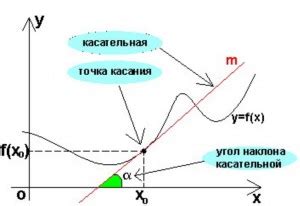
Угловой коэффициент – это число, показывающее, насколько быстро изменяется значение функции относительно изменения значений аргумента. Угловой коэффициент касательной к графику функции определяется как производная функции в точке касания.
Точка касания и угловой коэффициент могут быть полезны в различных областях математики и физики.
В геометрии точка касания играет важную роль в построении касательной линии к кривой. Зная угловой коэффициент касательной, можно определить угол, под которым она касается графика функции.
В физике точка касания может быть использована для определения момента, когда скорость изменения значения функции достигает нуля. Это может быть момент разворота движения или точка экстремума.
В анализе данных точка касания может помочь в определении точки пересечения двух или более функций. Зная значение функции и ее угловой коэффициент в точке касания, можно найти аргумент, при котором функции пересекаются.
Задачи на построение касательной

Построение касательной позволяет нам определить скорость изменения функции в заданной точке, а также найти наклон касательной и точку пересечения с осью абсцисс.
Для построения касательной необходимо выполнить следующие шаги:
- Найти точку, к которой будет построена касательная. Это может быть произвольная точка на графике функции или точка, заданная в условии задачи.
- Найти значение производной функции в данной точке. Это позволит нам определить наклон касательной.
- Используя найденное значение производной, построить уравнение прямой, проходящей через заданную точку и имеющей заданный наклон.
- Построить полученную прямую на графике функции.
Задачи на построение касательной могут быть различной сложности. Они могут предусматривать построение касательной к функции в точке экстремума, касательной к функции с использованием более сложных методов (например, метода дифференциалов) или построение касательной к параметрической функции.
Построение касательной имеет широкое применение в различных областях науки и техники, таких как физика, экономика, компьютерная графика. Кроме того, оно позволяет нам лучше понять поведение функции вблизи заданной точки и решать различные задачи, связанные с анализом и оптимизацией функций.
Приложения в физике и экономике

Касательная, параллельная оси абсцисс, играет важную роль в анализе графиков функций и имеет множество применений в физике и экономике. Рассмотрим некоторые из них:
- Физика:
- Определение скорости: касательная к графику зависимости координаты от времени показывает скорость тела. Наклон касательной определяет величину и направление скорости.
- Определение ускорения: измение наклона касательной позволяет определить ускорение тела.
- Определение силы: касательная к графику силы отклонения тела позволяет определить силу, действующую на тело.
- Определение работы: касательная к графику работы позволяет определить количество совершенной работы в зависимости от изменения координаты.
- Экономика:
- Предельные затраты: касательная к графику функции затрат позволяет определить предельные затраты на производство единицы товара.
- Маржинальный доход: касательная к графику функции дохода позволяет определить маржинальный доход от продажи единицы товара.
- Оптимальный объем производства: точка, где касательная к графику функции затрат пересекает касательную к графику функции дохода, определяет оптимальный объем производства, при котором доходы равны затратам.
Таким образом, касательная, параллельная оси абсцисс, является мощным инструментом для анализа графиков функций и нахождения важных физических и экономических параметров.



