Трапеция - это геометрическая фигура, которая имеет две параллельные стороны и две непараллельные стороны. Она также может иметь две диагонали, которые соединяют непараллельные стороны.
Одно из интересных свойств трапеции - когда одна из диагоналей является биссектрисой. Биссектриса - это прямая линия, которая делит угол пополам, разделяя его на два равных угла.
Когда диагональ в трапеции является биссектрисой, она делит противоположные стороны трапеции на две равные части. Это свойство позволяет решать различные геометрические задачи, связанные с трапецией, например, нахождение значений углов или сторон.
Использование свойства, когда диагональ является биссектрисой, может быть полезно при решении задач на геометрию, а также при построении и анализе различных фигур. Это одно из множества интересных свойств трапеции, которые помогают понять ее характеристики и особенности.
Что такое биссектриса диагонали трапеции?

Для того чтобы понять, что такое биссектриса диагонали трапеции, нужно вспомнить, что диагональ трапеции - это отрезок, соединяющий противоположные вершины трапеции. Из определения биссектрисы известно, что она делит угол между двумя сторонами на две равные части.
В случае с диагональю трапеции, биссектриса проходит через середину диагонали и перпендикулярна каждой из боковых сторон. Это значит, что длина отрезка диагонали между боковыми сторонами трапеции будет равна.
Биссектриса диагонали трапеции имеет важное свойство. Если провести перпендикуляры от середины диагонали к основаниям трапеции, они будут равны. Иными словами, биссектриса диагонали разделяет основания трапеции на две равные части.
| Свойства биссектрисы диагонали трапеции: | |
| 1. | Делит диагональ трапеции на две равные части. |
| 2. | Перпендикулярна каждой из боковых сторон трапеции. |
| 3. | Разделяет основания трапеции на две равные части. |
Таким образом, биссектриса диагонали трапеции является важной линией, которая делит диагональ на две равные части, перпендикулярна боковым сторонам трапеции и разделяет основания на две равные части.
Определение биссектрисы и диагонали трапеции

Диагональ трапеции, в отличие от параллельных сторон, не является боковой стороной и пересекает их. Она также создает четыре треугольника внутри трапеции - два меньших и два больших.
Биссектриса - это прямая линия, которая делит угол на две равные части. В случае трапеции, диагональ может являться биссектрисой, если она делит один из углов трапеции на две равные части. Тогда диагональ будет проходить через середину этого угла и делить его пополам.
Определение биссектрисы и диагонали трапеции играет важную роль в геометрии, анализе углов и нахождении различных свойств трапеции. Эти понятия помогают лучше понять геометрические формы и связи между сторонами и углами трапеции.
Как определить, является ли диагональ биссектрисой трапеции?

Сначала проверяем, пересекает ли диагональ трапецию. Если нет, то она точно не является биссектрисой. Если пересекает, то далее проверяем равенство углов.
Чтобы это сделать, можно использовать следующий алгоритм:
- Найдите высоту трапеции (прямую, проведенную из вершины трапеции к основанию параллельно боковой стороне).
- С помощью высоты разбейте диагонали трапеции на две части.
- Найдите углы между разбитыми частями диагонали и боковыми сторонами трапеции.
- Если найденные углы равны, то диагональ является биссектрисой трапеции.
Важно помнить, что в трапеции только одна диагональ может быть биссектрисой. Проверьте указанные условия для всех диагоналей трапеции, и вы сможете определить, является ли диагональ биссектрисой или нет.
Свойства биссектрисы диагонали трапеции
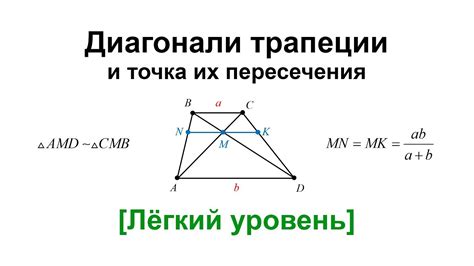
1. Расстояние от вершины трапеции до точки пересечения биссектрицы и противоположной стороны равно полусумме длин параллельных сторон трапеции.
Данное свойство означает, что прямая, являющаяся биссектрисой диагонали трапеции, является строительной линией, которая помогает определить ровные части противоположной стороны.
2. Биссектриса диагонали трапеции перпендикулярна боковым сторонам трапеции.
Это свойство означает, что биссектриса диагонали трапеции создает прямые углы с боковыми сторонами, что позволяет использовать ее для построения перпендикуляров внутри трапеции.
Свойства биссектрисы диагонали трапеции широко используются при решении задач, связанных с построением и нахождением свойств трапеции.
Геометрическое значение биссектрисы диагонали трапеции

Одно из геометрических значений биссектрисы диагонали трапеции состоит в том, что она является основанием равнобедренного треугольника. Если провести линию от вершины трапеции, лежащей на прямой, которая является продолжением диагонали, до точки пересечения биссектрисы и диагонали, то получится еще одна равнобедренная трапеция, вершины которой лежат на двух диагоналях трапеции и на биссектрисе.
Также биссектриса диагонали трапеции играет важную роль при построении высоты, опущенной из вершины трапеции. Если провести линию, перпендикулярную биссектрисе и проходящую через вершину трапеции, то эта линия будет являться высотой. При этом она будет делить биссектрису и диагональ трапеции на отрезки, пропорциональные высотам двух равнобедренных трапеций, образованных этой высотой.
Таким образом, геометрическое значение биссектрисы диагонали трапеции является ключевым для решения многих задач и построения геометрических фигур. Понимание этого значения позволяет легко разобраться в свойствах и особенностях трапеции и использовать их в практике.
Примеры использования биссектрисы диагонали трапеции в решении задач

Один из примеров использования биссектрисы диагонали трапеции может быть следующим: предположим, что у нас есть трапеция ABCD, в которой диагональ AC является ее биссектрисой. Задача состоит в том, чтобы найти угол между боковой стороной AD и основанием BC.
Для решения этой задачи мы можем использовать свойство биссектрисы диагонали. Поскольку AC является биссектрисой диагонали, то угол BAC равен углу CAD. Поскольку AD является боковой стороной трапеции, то угол BAC равен углу BCA. Таким образом, угол между боковой стороной AD и основанием BC является полусуммой углов BCA и CAD.
Таким образом, мы можем использовать биссектрису диагонали трапеции для нахождения угла между боковой стороной и основанием. Этот пример демонстрирует, что знание особенностей биссектрисы диагонали трапеции может быть полезно при решении геометрических задач.



