Математические функции ограничены как снизу, так и сверху, когда существуют нижняя и верхняя границы их значения. Это может быть полезным свойством при анализе функций и решении различных задач. Знание ограниченности функции позволяет получить больше информации о ее поведении и свойствах.
Изучение ограниченности функции включает определение нижней и верхней границы, а также нахождение точек экстремума. Нижняя граница функции – это наименьшее значение, которое она может достигнуть, а верхняя граница – это наибольшее значение. Если функция имеет как нижнюю, так и верхнюю границу, она называется ограниченной сверху и снизу.
Ограниченность функции может быть полезной не только для математических исследований, но и для решения прикладных задач. Например, ограниченность функции может быть использована при оптимизации процессов или поиске экстремальных значений. Кроме того, знание нижней и верхней границы функции может помочь при анализе ее поведения в различных ситуациях и принятии решений на основе этого анализа.
Когда функция имеет верхний и нижний предел: основные концепции и лучшие примеры
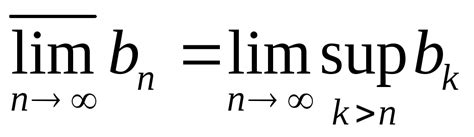
Основные концепции связанные с функциями ограниченными сверху и снизу включают:
- Верхний предел: это наибольшее значение, которое функция может достичь в пределах определенного диапазона. Если функция ограничена сверху, мы говорим, что у нее есть верхний предел.
- Нижний предел: это наименьшее значение, которое функция может достичь в пределах определенного диапазона. Если функция ограничена снизу, мы говорим, что у нее есть нижний предел.
- Диапазон ограничений: это интервал значений, в пределах которого функция ограничена. Он может быть задан числами или интервалом от минимального до максимального значения.
Давайте рассмотрим несколько примеров функций с верхним и нижним пределом:
- Функция
f(x) = x^2имеет верхний предел, так как значения функции растут с увеличением аргумента. Однако, у нее нет нижнего предела, так как значения функции могут быть отрицательными. - Функция
g(x) = sin(x)имеет верхний и нижний предел, так как значения синуса всегда находятся в диапазоне от -1 до 1. - Функция
h(x) = 3имеет и верхний, и нижний предел, так как она всегда возвращает одно и то же значение вне зависимости от аргумента.
Теперь вы понимаете, что значит, когда функция ограничена сверху и снизу, и можете легко определить наличие верхнего и нижнего предела для различных функций.
Что такое ограниченная функция?

Формально, функция f(x) называется ограниченной, если существуют числа M и m, такие что m ≤ f(x) ≤ M для всех x в заданной области.
Ограниченные функции часто встречаются в математике и физике. Их свойства и поведение можно изучать и анализировать с использованием различных методов, таких как графики функций, производные и интегралы.
Для иллюстрации, рассмотрим пример ограниченной функции. Функция f(x) = sin(x) ограничена сверху и снизу значениями -1 и 1 соответственно. Это означает, что -1 ≤ sin(x) ≤ 1 для всех значений x.
Таблица ниже показывает значения функции sin(x) и ее ограниченность в определенном диапазоне значений x.
| x | sin(x) |
|---|---|
| 0 | 0 |
| π/6 | 1/2 |
| π/2 | 1 |
| 7π/6 | -1/2 |
| 3π/2 | -1 |
Как видно из таблицы и графика функции sin(x), значения функции находятся в пределах от -1 до 1 для всех значений x.
Важность ограниченных функций в математике и физике
Ограниченность функции означает, что ее значения ограничены сверху и снизу определенными значениями. Это позволяет исследовать и анализировать функции, определять их свойства и поведение в различных условиях.
В математике ограниченные функции широко применяются для решения задач, связанных с определением экстремумов функций, поиска границ и интервалов, на которых функция обладает определенными свойствами. Они также позволяют установить ограничения на значения функций при решении уравнений и неравенств.
В физике ограниченные функции встречаются при моделировании различных процессов, включая движение тел, динамику систем и прочие физические явления. Ограничивая функции сверху и снизу определенными значениями, физики могут предсказывать и анализировать поведение системы и прогнозировать результаты экспериментов.
Ограниченные функции помогают упростить сложные проблемы и сделать их более понятными и доступными для исследования. Благодаря ограничениям, ученые могут получать точные и надежные результаты, опираясь на строгие математические и физические принципы.
Использование ограниченных функций полезно не только для ученых и математиков, но и для людей в повседневной жизни. Например, ограниченная функция может использоваться для моделирования поведения финансовых рынков, предсказания изменений температуры воздуха или оценки пропускной способности сети передачи данных.
Таким образом, понимание и использование ограниченных функций являются важными аспектами в математике и физике, которые позволяют ученым и исследователям более полно и точно анализировать и предсказывать различные явления и процессы в природе и обществе.
Примеры функций с верхним и нижним ограничениями
Функции, ограниченные сверху и снизу, встречаются во многих областях математики и физики. Они играют важную роль в оптимизации, анализе данных и моделировании.
Примером функции с верхним ограничением может быть сигмоидная функция, которая ограничена значениями 0 и 1. Она широко используется в теории нейронных сетей и математической логике. Формула для этой функции выглядит следующим образом:
f(x) = 1 / (1 + e-x)
где x - любое вещественное число. Заметим, что при x → +∞, f(x) → 1, а при x → -∞, f(x) → 0.
Примером функции с нижним ограничением может быть функция Гаусса, или нормальное распределение. Чаще всего она записывается следующим образом:
f(x) = (1 / (σ√2π)) * e-((x-μ)² / (2σ²))
где μ - математическое ожидание, σ - стандартное отклонение. Значения функции Гаусса положительны при всех значениях x, и они образуют колоколообразный график с максимальным значением в точке x = μ. В прикладных задачах нормальное распределение широко используется для анализа и моделирования данных.
Это лишь два примера функций с верхним и нижним ограничениями из бесконечного списка. Ограничения могут быть различными и зависят от конкретной задачи или приложения. Важно понимать, что ограничения функций могут существенно влиять на их свойства и возможности использования в различных областях науки и техники.
Практическое применение ограниченных функций в реальной жизни
Ограниченные функции, которые имеют как верхнюю, так и нижнюю границу, имеют множество практических применений в реальной жизни. Эти функции встречаются в различных областях науки, техники и экономики, и их использование позволяет решить множество задач и оптимизировать процессы.
Одним из примеров практического применения ограниченных функций является задача планирования ресурсов в производственных предприятиях. В этой задаче необходимо определить оптимальное распределение ресурсов (например, рабочего времени или материалов) для достижения максимальной производительности при соблюдении ограничений, связанных с бюджетом или доступностью ресурсов. Для решения этой задачи могут использоваться ограниченные функции, которые описывают зависимость между вводом ресурсов и выходом продукции.
Еще одним примером практического применения ограниченных функций является финансовое планирование в компаниях. Когда компания разрабатывает бюджет или строит финансовые модели, она должна учесть ограничения, связанные с доступностью финансовых ресурсов. Например, функция ограничения может описывать долю доходов, которую компания обязана потратить на определенные расходы. Использование ограниченных функций в финансовом планировании помогает компаниям оптимизировать расходы и достичь финансовой устойчивости.
Также ограниченные функции применяются в медицине для определения дозировки лекарств. Врачи используют ограниченные функции для определения максимальной и минимальной дозы лекарства, которую пациент может принять в зависимости от его веса и состояния здоровья. Это помогает предотвратить проблемы, связанные с передозировкой или недостаточной эффективностью лекарства.
Таким образом, ограниченные функции имеют широкое применение в реальной жизни и помогают решать множество задач в различных областях. Их использование позволяет оптимизировать процессы, достичь эффективности и избежать проблем, связанных с нарушением ограничений.



