Знание о том, как функция меняется величиной в зависимости от переменной, играет важную роль в математике и ее приложениях. Ответ на вопрос, когда функция растет, а когда убывает, помогает понять ее поведение и использовать эту информацию для решения различных задач.
В математике существует несколько правил, которые позволяют определить, как меняется функция в зависимости от значения переменной. Одно из самых простых правил - это правило производной функции. Если производная функции положительна, то функция возрастает, если она отрицательна - то функция убывает. Но это не единственное правило.
Существуют функции, у которых может быть разрыв, точки экстремума или точки разрыва. В таких случаях нужно анализировать функцию на каждом отрезке непрерывности и учитывать особенности ее поведения. Кроме того, важно помнить о влиянии начальных условий и границ области определения функции. При анализе функции необходимо учитывать все эти аспекты и применять соответствующие правила.
Для лучшего понимания того, как функции могут меняться, рассмотрим несколько примеров. Например, рассмотрим функцию квадратного корня sqrt(x). Эта функция увеличивается с увеличением значения аргумента x, но только при неотрицательных значениях. Это связано с тем, что квадратный корень отрицательного числа не определен. В других примерах можно изучить функции полиномов, экспоненты и логарифмов, их поведение и окрестности точек разрыва.
Функция: определение и особенности ее роста или убывания

Функция, в математике, представляет собой отношение между двумя множествами, которое каждому элементу одного множества сопоставляет элементы другого множества. Функции широко используются для описания зависимостей и взаимосвязей между переменными в различных областях науки и инженерии.
Одним из основных понятий, связанных с функциями, является их рост или убывание. Рост функции означает, что ее значения увеличиваются с увеличением аргумента, тогда как убывание функции означает, что ее значения уменьшаются с увеличением аргумента.
Функция может иметь различные формы роста или убывания. Например, функция может возрастать монотонно, то есть ее значения увеличиваются постоянно при увеличении аргумента. Функция может также убывать монотонно, когда ее значения уменьшаются постоянно при увеличении аргумента.
Однако функции могут иметь и более сложные формы роста или убывания. Например, функция может иметь точку поворота, где она переходит из роста в убывание или наоборот. Функция может иметь также различные участки с различной скоростью роста или убывания. Например, функция может иметь начальный участок с быстрым ростом, который затем замедляется.
Важно понимать особенности роста или убывания функции, чтобы полноценно использовать ее в анализе данных или при работе с математическими моделями. Изучение роста и убывания функций является ключевым в математике и имеет множество применений в науке и технике.
Основные принципы функции и ее изменения на протяжении времени

Одним из основных принципов функции является возрастание или убывание ее значения при изменении переменной или переменных. Когда функция растет, это означает, что ее значения увеличиваются при увеличении переменной или переменных. Например, если функция представляет собой зависимость дохода от количества отработанных часов, то по мере увеличения отработанных часов доход будет расти.
Напротив, когда функция убывает, это означает, что ее значения уменьшаются при увеличении переменной или переменных. Например, если функция представляет собой зависимость расходов от количества продукции, то по мере увеличения производства расходы будут убывать.
Изменения функции могут быть различной природы. Некоторые функции могут изменяться постепенно, плавно переходя от убывающего к возрастающему режиму или наоборот. Другие функции могут иметь точки перегиба, где сменяется направление изменения. Например, функция сначала может расти, затем достигнув определенной точки, начинает убывать. Такие точки перегиба, также называемые точками экстремума, могут быть максимальными или минимальными значениями функции.
Определение принципов и изменений функции является важным элементом анализа данных и моделирования реальных процессов. Понимание основных принципов функции и ее изменений на протяжении времени позволяет прогнозировать ее поведение и принимать обоснованные решения в практических задачах.
Когда функция возрастает: причины и примеры

Математическая функция называется возрастающей, если при увеличении аргумента значения функции также увеличиваются. Возрастание функции может зависеть от различных факторов, которые влияют на ее поведение.
Одной из причин возрастания функции может быть прямая зависимость между аргументом и значением функции. Например, функция y = x возрастает, так как при увеличении значения x значение y также увеличивается.
Высокий коэффициент наклона может также быть причиной возрастания функции. Например, функция y = 2x возрастает быстрее, чем функция y = x, так как ее график имеет более крутой наклон.
Еще одной причиной возрастания функции может быть положительная производная. Если производная функции положительна на определенном интервале, то это означает, что значения функции увеличиваются на этом интервале. Например, функция y = x^2 возрастает на интервале x > 0, так как ее производная y' = 2x положительна для положительных значений x.
Возрастание функции важно понимать при решении задач на определение экстремумов функции или поиске значений, которые достигаются функцией. Знание того, когда функция возрастает, помогает определить, в каких интервалах нужно искать эти значения или экстремумы.
Примеры возрастающих функций:
- Линейная функция: y = x (график функции является прямой, наклоненной под углом 45 градусов).
- Степенная функция: y = x^n, где n > 1 (график функции имеет положительный наклон и становится еще круче с увеличением значения n).
- Экспоненциальная функция: y = a^x, где a > 1 (график функции стремительно возрастает с увеличением значения x).
Знание правил и примеров возрастания функций позволяет более точно анализировать и решать задачи, связанные с математическими функциями и их свойствами.
Какие факторы способствуют убыванию функции: анализ и применение

При изучении функций в математике важно обратить внимание не только на их возрастание, но и на убывание. Знание факторов, которые способствуют убыванию функции, может быть полезным при анализе графиков и решении уравнений.
Один из основных факторов, который приводит к убыванию функции, - это отрицательный коэффициент при степени переменной. Если в функции присутствует отрицательная степень переменной, то при увеличении значения переменной, значение функции будет убывать. Например, функция f(x) = 1/x имеет отрицательный коэффициент при степени переменной x, и ее значение будет убывать при увеличении значения переменной.
Еще одним фактором, который способствует убыванию функции, является наличие отрицательного коэффициента перед переменной в линейной функции. Если функция имеет вид f(x) = -ax + b, где a и b - константы, то при увеличении значения x, значение функции будет убывать. Например, функция f(x) = -2x + 3 имеет отрицательный коэффициент перед переменной x, и ее значение будет убывать при увеличении значения x.
Также следует отметить, что использование отрицательных коэффициентов при добавлении или вычитании слагаемых в функции может способствовать ее убыванию. Например, функция f(x) = x^2 - 2x - 3 имеет отрицательные коэффициенты перед слагаемыми 2x и 3, и ее значение будет убывать при увеличении значения x.
Выявление и анализ этих факторов поможет лучше понять поведение функций и использовать их на практике. Например, знание факторов, способствующих убыванию функции, может быть полезно при определении максимальных и минимальных значений функции, поиске корней уравнений, а также в других математических и инженерных приложениях.
Примеры роста функции в реальной жизни и бизнесе
Математические функции могут быть применены во многих областях реальной жизни и бизнесе для определения роста чего-либо. Например, в маркетинге можно использовать функции для предсказания роста продаж товара или услуги.
Если провести анализ данных продаж за определенный период времени, можно вычислить функцию роста, которая позволит предсказать будущие продажи. Это позволит бизнесу планировать свою деятельность, определять бюджеты и ресурсы на основе ожидаемого роста.
Также функции роста могут использоваться в экономике для анализа различных показателей, таких как ВВП, доходы, инфляция и безработица. При помощи функций роста экономисты могут определить тренды и прогнозировать изменения в этих показателях. Это позволяет правительствам и организациям принимать решения, связанные с экономическим развитием и политикой.
Функции роста также играют важную роль в науке и технике. Например, при моделировании распространения эпидемий или популяционного роста, функции могут быть использованы для предсказания будущих тенденций. Это помогает ученым и инженерам принимать решения, связанные с общественным здравоохранением и экологией.
Ситуации, когда функция стремится к убыванию: детальное описание

Существуют определенные ситуации, когда функция убывает, то есть значение функции уменьшается при увеличении значения аргумента. Ниже приведены несколько примеров таких ситуаций.
Первый пример - экспоненциальная функция с отрицательным показателем. Когда показатель экспоненты имеет отрицательное значение, функция будет убывать при увеличении значения аргумента. Например, функция y = 2^(-x) будет убывать при увеличении значения x.
Второй пример - функция с отрицательным коэффициентом при степенном выражении. Если в функции имеется степенное выражение вида x^n, и коэффициент n является отрицательным числом, то функция будет убывать при увеличении значения x. Например, функция y = -x^2 будет убывать при увеличении значения x.
Третий пример - логарифмическая функция с базой больше 1. Если база логарифма больше 1, то функция будет убывать при увеличении значения аргумента. Например, функция y = log_2(x) будет убывать при увеличении значения x.
Таким образом, в определенных ситуациях функция может стремиться к убыванию при увеличении значения аргумента. Это важно учитывать при анализе графиков функций и решении математических задач.
Как предсказать рост или убывание функции: методы и приемы
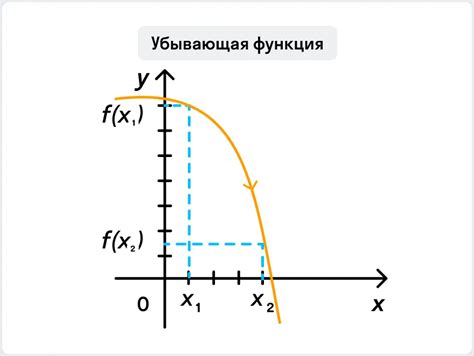
1. Исследование знака производной
Производная функции показывает наклон касательной к графику функции в данной точке. Если производная положительна, то функция возрастает, если отрицательна - функция убывает. Таким образом, исследование знака производной может помочь определить, когда функция растет или убывает.
2. Анализ экстремумов функции
Экстремумы функции - это точки, в которых функция достигает локального максимума (пик) или минимума (яма). Частные случаи экстремумов - точки, в которых функция достигает глобального максимума или минимума. Исследование экстремумов позволяет определить, когда функция растет или убывает в зависимости от их положения.
3. Анализ поведения функции на бесконечности
Исследование поведения функции на бесконечности может также помочь в определении роста или убывания функции. Например, если функция стремится к положительной бесконечности при стремлении аргумента к положительной бесконечности, то функция растет; если функция стремится к отрицательной бесконечности, то функция убывает.
4. Использование дополнительных методов
В зависимости от конкретного случая, можно использовать и другие методы и приемы для предсказания роста или убывания функции. Например, анализ второй производной, понятия выпуклости и вогнутости, анализ точек перегиба и т.д. Важно выбрать наиболее подходящий метод в каждом случае и правильно его применить.



