Одним из основных понятий математического анализа является возрастание и убывание функции. Это понятие важно для понимания многих аспектов математики, а также для решения различных задач.
Возрастание функции означает, что ее значения стремительно растут с увеличением аргумента. Иными словами, график функции идет вверх. Убывание же функции подразумевает, что значения функции уменьшаются с увеличением аргумента. График функции при этом направлен вниз.
Для определения возрастания или убывания функции используются различные методы. Если необходимо определить, возрастает ли функция на заданном промежутке, достаточно вычислить производную и проанализировать ее знак. Если производная на данном промежутке положительна, то функция возрастает. Если же производная отрицательна, то функция убывает. Если производная равна нулю, функция имеет экстремум (максимум или минимум) и на этом промежутке ни возрастает, ни убывает.
Определение и принципы возрастания и убывания функции

В математике функция называется возрастающей, если с увеличением значения аргумента значение функции также увеличивается. В противном случае, функция называется убывающей.
Определение возрастания и убывания функции основано на понятии производной. Если производная функции положительна на всей области определения, то функция возрастает. Если производная функции отрицательна на всей области определения, то функция убывает.
Также можно определить возрастание и убывание функции с помощью графика. Если график функции непрерывно и изображает восходящую кривую, то функция возрастает. Если график функции непрерывно и изображает нисходящую кривую, то функция убывает.
Применение принципов возрастания и убывания функции позволяет анализировать ее поведение и находить экстремумы, точки перегиба и другие особенности графика. Это важные инструменты для решения задач в различных областях, таких как физика, экономика, статистика и т.д.
Что такое возрастание и убывание функции

В математике функция называется возрастающей, если с увеличением значения аргумента функции ее значение также возрастает. Иными словами, если при увеличении аргумента значения функции становятся все больше, то функция называется возрастающей.
На графике возрастающая функция представлена в виде прямой линии, идущей вверх слева направо.
Однако функция может быть и убывающей. Убывающая функция - это такая функция, при которой с увеличением значения аргумента значения функции становятся все меньше. Если при увеличении аргумента значения функции уменьшаются, то функцию называют убывающей.
На графике убывающая функция представлена в виде прямой линии, идущей вниз слева направо.
Возрастание и убывание функции являются важными концепциями в математике и находят применение в различных областях, включая экономику, физику, статистику и т.д.
Критерии возрастания и убывания функции

Критерии возрастания и убывания функции позволяют определить, в каких интервалах ее значения увеличиваются или уменьшаются.
Для определения возрастания или убывания функции необходимо:
- Найти производную функции.
- Решить неравенство производной.
- На основе решенного неравенства определить интервалы возрастания и убывания функции.
Если производная функции положительна на определенном интервале, то функция возрастает на этом интервале. Если производная функции отрицательна на определенном интервале, то функция убывает на этом интервале.
Если производная функции равна нулю на определенном интервале, необходимо провести дополнительные исследования, так как на данном интервале возможно наличие экстремумов функции.
| Производная функции | Интервалы возрастания функции | Интервалы убывания функции |
|---|---|---|
| Положительная | Отрицательная | Положительная |
| 0 | Неопределены | Неопределены |
| Отрицательная | Положительная | Отрицательная |
Критерии возрастания и убывания функции являются важными инструментами при анализе и исследовании функций, позволяющими получить информацию о их поведении и основных характеристиках.
Принципы возрастания и убывания функции

При изучении функций в математике очень важно понимать их характер изменения на заданном интервале. Поэтому особое внимание уделяется определению того, когда функция возрастает или убывает. Существуют несколько принципов и условий, которые помогают определить изменение функции:
1. Первый производный. Один из основных способов определить характер изменения функции является исследование ее первой производной. Если первая производная положительна на интервале, то функция возрастает на этом интервале. Если первая производная отрицательна, то функция убывает. Если первая производная равна нулю, то имеется точка экстремума - максимума или минимума функции.
2. Дифференциальное исчисление. Изучение характера изменения функции также связано с дифференциальным исчислением. Если производная функции положительна на всем интервале и не равна нулю, то функция строго возрастает на этом интервале. Если производная функции отрицательна на всем интервале и не равна нулю, то функция строго убывает.
3. Таблицы значений. Еще один способ определить характер изменения функции - составить таблицу значений и проанализировать изменение функции. Если значения функции увеличиваются при увеличении аргумента, то функция возрастает. Если значения функции уменьшаются при увеличении аргумента, то функция убывает.
Примеры возрастания и убывания функции
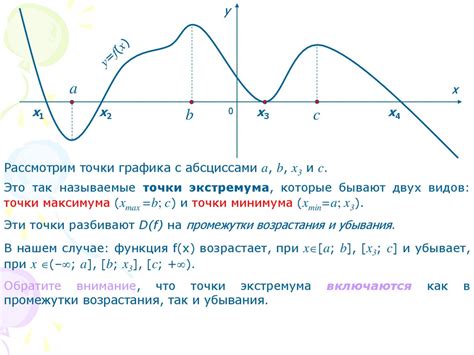
Возьмем некоторые примеры функций и рассмотрим их поведение на интервалах.
Пример 1:
Рассмотрим функцию f(x) = 2x + 3.
На интервале отрицательных значений x, функция возрастает. Например, при x=-2 и x=-1 значение функции соответственно равно -1 и 1.
На интервале положительных значений x, функция также возрастает. Например, при x=1 и x=2 значение функции соответственно равно 5 и 7.
Пример 2:
Рассмотрим функцию g(x) = x^2.
На интервале отрицательных значений x, функция также возрастает. Например, при x=-2 и x=-1 значение функции соответственно равно 4 и 1.
На интервале положительных значений x, функция также возрастает. Например, при x=1 и x=2 значение функции соответственно равно 1 и 4.
Пример 3:
Рассмотрим функцию h(x) = 1/x при x > 0.
На интервале положительных значений x, функция убывает. Например, при x=1 и x=2 значение функции соответственно равно 1 и 0.5.
Пример 4:
Рассмотрим функцию i(x) = -x^3.
На интервале отрицательных значений x, функция убывает. Например, при x=-2 и x=-1 значение функции соответственно равно -8 и -1.
На интервале положительных значений x, функция также убывает. Например, при x=1 и x=2 значение функции соответственно равно -1 и -8.



