Математика - наука, которая изучает пространственные и количественные отношения. В школе мы изучаем различные разделы математики, включая алгебру и геометрию. В геометрии особое внимание уделяется изучению графиков. График функции - это графическое представление зависимости одной величины от другой.
Если графики двух функций имеют общую точку пересечения, то это означает, что при соответствующем значении аргумента значения функций равны. В этом случае у нас есть решение системы уравнений, соответствующих этим функциям. Параллельные графики, напротив, не имеют общих точек пересечения и соответствующие функции не имеют общих значений для какого-либо аргумента.
Правила взаимного положения графиков в математике
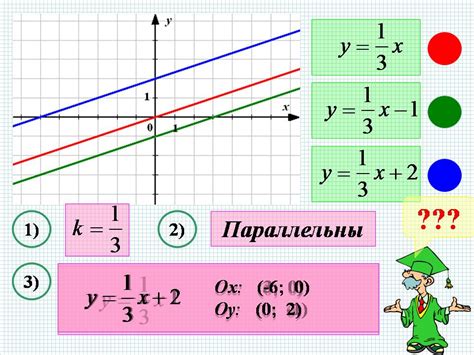
Понимание взаимного положения графиков функций играет важную роль в математике и позволяет нам анализировать и предсказывать их свойства и характеристики. В этом разделе мы рассмотрим правила для определения, когда графики функций параллельны или пересекаются.
1. Параллельные графики
Два графика функций называются параллельными, если они имеют одинаковый наклон и не пересекаются.
- Если две функции представлены линейными уравнениями вида y = kx + b, где k - коэффициент наклона, то они параллельны, если и только если их коэффициенты наклона равны, то есть k₁ = k₂.
- Если две функции заданы в виде графиков кривых, то они параллельны, если у них в каждой точке совпадают касательные.
2. Пересекающиеся графики
Графики функций пересекаются, если они имеют общие точки пересечения. Это означает, что значения функций в данных точках равны.
- Если две функции представлены линейными уравнениями вида y = kx + b, то они пересекаются в точке (x, y), где значения x и y являются решением системы уравнений.
- Если две функции заданы в виде графиков кривых, то они пересекаются в точках, где координаты x и y удовлетворяют уравнению каждой функции.
Взаимное положение графиков функций является важным инструментом для анализа и понимания их поведения. Знание правил определения параллельных и пересекающихся графиков позволяет нам лучше представлять и использовать математические функции в реальных ситуациях.
Когда графики параллельны?

Графики называются параллельными, если они представляют собой прямые линии, которые имеют одинаковый наклон. В других случаях, когда графики имеют различные наклоны, они будут пересекаться в какой-то точке.
Следующие случаи могут указывать на параллельность графиков:
- Графики имеют одинаковые наклоны и не пересекаются ни в одной точке.
- Уравнения графиков представляют собой одинаковые прямые линии.
- Графики имеют одинаковый угол наклона и параллельны друг другу во всех точках.
Параллельные графики обычно являются индикатором отсутствия взаимосвязи между двумя переменными. Они могут представлять собой различные величины, которые не зависят друг от друга или иметь разные интерпретации в контексте проблемы. Понимание природы параллельных графиков позволяет установить отсутствие влияния одной переменной на другую.
Когда графики пересекаются?

Графики функций пересекаются, когда значения функций в определенных точках равны. В математике эти точки называются пересечениями или корнями функций.
Существует несколько способов определить, пересекаются ли графики функций:
- Метод подстановки. Для этого нужно приравнять значения функций и решить полученное уравнение.
- Графический метод. Этот метод основан на построении графиков функций и определении их пересечений.
- Аналитический метод. С помощью аналитического метода можно определить пересечение графиков, находя точки, в которых функции имеют одинаковые значения.
Кроме того, графики функций могут пересекаться в точках экстремумов функций, таких как максимумы и минимумы. Эти точки определены как точки, где производные функций равны нулю или не существуют.
Пересечение графиков функций позволяет определить точки, где значения функций равны и где происходят изменения взаимного положения графиков. Это важное понятие в математике и имеет множество применений в различных областях, таких как физика, экономика и инженерия.
Понятие точки пересечения графиков
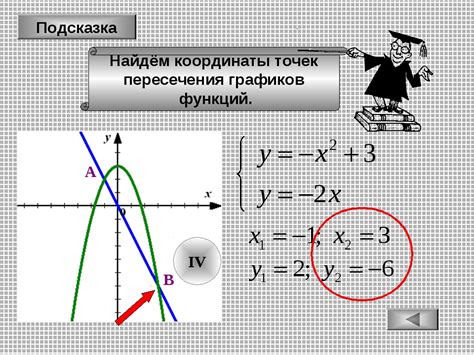
Если два графика имеют общую точку пересечения, то это означает, что значения переменных в этой точке удовлетворяют уравнениям, заданным каждым из графиков. В математическом плане, точка пересечения является решением системы уравнений, которые представляют собой уравнения каждого из графиков.
Точка пересечения может быть единственной, если графики пересекаются только в одной точке. Однако, они также могут иметь несколько точек пересечения, если графики пересекаются в нескольких местах. В некоторых случаях, графики могут быть параллельными и не иметь общих точек пересечения.
Определение точки пересечения графиков является важным понятием в аналитической геометрии и визуализации данных. Оно позволяет нам понять, как связаны между собой различные функции и исследовать их взаимное положение и взаимодействие.
Как определить количество точек пересечения графиков?

Точки пересечения графиков играют важную роль в анализе и изучении функций. Они определяются как точки, в которых графики двух функций пересекаются. При определении количества точек пересечения графиков необходимо учитывать их природу и тип функций, которые они представляют.
Если рассматривать графики линейных функций, то количество точек пересечения может быть определено исходя из их уравнений. Для этого нужно решить систему линейных уравнений, составленных из уравнений графиков. Количество решений системы будет равно количеству точек пересечения.
В случае графиков парабол или других квадратичных функций количество точек пересечения определяется особым образом. Если уравнения функций не имеют общих коэффициентов и дискриминант уравнения, полученного при приравнивании функций друг к другу, положителен, то графики будут пересекаться в двух точках. Если дискриминант равен нулю, то графики будут касаться в одной точке. И, наконец, если дискриминант отрицателен, то графиков не будет пересечься.
Для функций других типов, таких как экспоненциальные или логарифмические функции, количество точек пересечения может быть определено методами математического анализа функций. Для этого можно использовать графический метод, вычислительные методы или алгоритмы решения нелинейных уравнений.
Таким образом, определение количества точек пересечения графиков зависит от типа и природы функций. Для линейных функций можно решить систему уравнений, для парабол и квадратичных функций можно использовать дискриминант, а для функций других типов необходимо применять специальные методы и алгоритмы.
Как определить, что графики не пересекаются и не параллельны?

Если графики не пересекаются, то их уравнения не имеют общих точек. В этом случае коэффициенты наклона обоих графиков должны быть равными, но свободные члены должны отличаться. Например, уравнения графиков y = 2x + 1 и y = 2x + 3 задают параллельные прямые, так как их коэффициенты наклона равны, а свободные члены отличаются.
Если графики параллельны, то их уравнения имеют одинаковые коэффициенты наклона и свободные члены. Например, уравнения графиков y = 2x + 1 и y = 2x + 1 задают параллельные прямые, так как их коэффициенты наклона и свободные члены совпадают.
Таким образом, чтобы определить, что графики не пересекаются и не параллельны, необходимо проверить, равны ли коэффициенты наклона и отличаются ли свободные члены в уравнениях графиков.
Влияние коэффициентов наклона графиков на их взаимное положение
Коэффициент наклона графика представляет собой отношение изменения значения переменной y к изменению значения переменной x. Он определяет наклон линии, которую представляет график.
Если у двух графиков коэффициенты наклона равны, то они параллельны и не пересекаются. Это означает, что изменение одной переменной не влияет на изменение другой переменной и их значения остаются постоянными при изменении независимой переменной.
Однако, когда коэффициенты наклона графиков различаются, они будут иметь разные наклоны и могут пересекаться. Если коэффициент наклона одного графика больше нуля, а другого меньше нуля, то графики пересекаются и имеют общую точку пересечения.
Кроме того, когда коэффициент наклона одного графика равен нулю, а другого не равен нулю, они также могут пересекаться. При этом происходит пересечение горизонтальной и наклонной линий, и точка пересечения будет являться решением системы уравнений, описывающих графики.
Таким образом, коэффициенты наклона графиков играют важную роль в их взаимном положении, определяя возможность их параллельности или пересечения. Понимание этого влияния позволяет более точно анализировать и интерпретировать графики функций и систем уравнений.
Практические примеры положения графиков
1. Графики, параллельные по горизонтали
Если два графика находятся на одном уровне и не пересекаются, то они являются параллельными по горизонтали. Например, уравнения графиков могут быть x = 2 и x = 4. В этом случае, вертикальные линии, соответствующие графикам, будут идти параллельно и находиться на одном уровне.
2. Графики, параллельные по вертикали
Если два графика находятся на разных уровнях, но не пересекаются, то они являются параллельными по вертикали. Например, уравнения графиков могут быть y = 3 и y = 3 + 2. В этом случае, горизонтальные линии, соответствующие графикам, будут идти параллельно, но находиться на разных уровнях.
3. Графики, пересекающиеся в одной точке
Если два графика пересекаются в одной точке, то они имеют общее решение. Например, уравнения графиков могут быть y = x и y = -x + 2. В этом случае, график y = x представляет собой наклонную прямую, а график y = -x + 2 - наклонную прямую, которая пересекается с первой в точке (1, 1).
4. Графики, не пересекающиеся
Если два графика не пересекаются ни в одной точке, то они не имеют общего решения. Например, уравнения графиков могут быть y = x^2 и y = x + 2. В этом случае, график y = x^2 представляет собой параболу, а график y = x + 2 - наклонную прямую, которая не пересекается с параболой.
Важно помнить, что положение графиков определяется не только уравнениями, но и их коэффициентами и степенями. Также следует отметить, что в некоторых случаях графики могут пересекаться в нескольких точках или быть параллельными как по горизонтали, так и по вертикали.



