Бесконечно малая переменная an широко используется в математике, особенно в анализе. Она представляет собой переменную, которая стремится к нулю при приближении ее аргумента к некоторому конечному значению. Хотя понятие бесконечно малой в математике может быть достаточно сложным для понимания, оно играет важную роль в различных механизмах и формулах.
Изначально понятие бесконечно малой переменной было введено математиками в XVII веке для разработки системы непрерывного вычисления. С течением времени оно приобрело большую популярность и нашло применение в различных разделах математики, начиная от анализа и дифференциальных уравнений до теории вероятностей.
Когда переменную an называют бесконечно малой, это означает, что она стремится к нулю в пределе. В то же время, важно отметить, что бесконечно малая переменная an не является нулем сама по себе, она только стремится к нулю. Это позволяет нам использовать ее в различных вычислениях и применять специальные методы, основанные на понятии предела.
Определение бесконечно малой переменной "an"

Бесконечно малая переменная "an" представляет собой понятие из математического анализа, которое используется для описания бесконечно малого изменения значения функции при стремлении независимой переменной к некоторому числу или бесконечности.
Математически, бесконечно малая переменная "an" обозначает, что приближение значения функции к данной переменной будет близким к нулю. В других словах, "an" представляет собой элемент последовательности, который стремится к нулю, когда "n" стремится к бесконечности.
Определение бесконечно малой переменной "an" часто используется при изучении пределов функций и дифференциального исчисления. Благодаря бесконечно малым переменным возможно описывать скорость изменения функции и её производную в конкретной точке.
В математических выражениях бесконечно малая переменная "an" обычно обозначается символом "an" и заключается в пределах некоторой последовательности. Её значение и свойства могут быть определены при помощи различных методов и аксиом математического анализа.
| Обозначение | Описание |
|---|---|
| "an" | Бесконечно малая переменная |
| "n" | Независимая переменная |
Использование бесконечно малой переменной "an" позволяет удобным способом описывать и анализировать поведение функций и их производных в определенных точках. Умение работать с бесконечно малыми переменными является важным навыком в математике и науке, позволяющим решать различные задачи и ставить новые открытия.
Области применения переменной "an"

Переменная "an", как бесконечно малая величина, находит применение в различных областях науки и математики. Ее использование позволяет упростить вычисления и улучшить точность результатов.
В физике переменная "an" может быть использована для описания изменений величин в момент времени, когда происходит бесконечно малое приращение. Например, она может использоваться для определения скорости тела при моментальном изменении времени.
В математике переменная "an" может применяться для исследования функций и их свойств. Она может помочь в определении производной функции в определенной точке, что позволяет анализировать ее поведение на малых интервалах.
Переменная "an" также имеет свое применение в экономике и финансовой математике. Она может использоваться для анализа изменений стоимости активов и определения рисков и потенциальных доходов в бесконечно малых промежутках времени.
Основные свойства и характеристики "an"
Главное свойство "an" заключается в том, что она стремится к нулю при приближении к бесконечности. Это означает, что любое число, разделенное на "an", будет стремиться к бесконечности.
an может также иметь другие характеристики, которые зависят от контекста и конкретной математической задачи. В некоторых случаях, "an" может быть монотонно убывающей или возрастающей последовательностью, а в других - может быть ограниченной сверху или снизу.
Важно понимать, что "an" является концептуальным математическим объектом и имеет строгое определение в рамках математического анализа. "an" используется для решения различных математических проблем и моделирования сложных процессов.
Математические операции с бесконечно малой переменной "an"
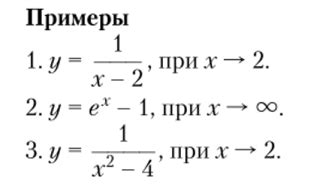
Переменная "an" часто используется при изучении пределов функций. В математике существуют различные операции, которые можно выполнять с бесконечно малой переменной "an".
Одной из наиболее распространенных операций является сложение или вычитание бесконечно малой переменной "an" из другой переменной или последовательности. Например, если у нас есть последовательность "bn", и мы хотим вычислить предел "bn - an", то достаточно вычесть из каждого элемента последовательности "bn" соответствующий элемент последовательности "an".
| Операция | Выражение | Результат |
|---|---|---|
| Сложение | bn + an | Результатом будет новая последовательность, где каждый элемент получается путем сложения соответствующих элементов последовательности "bn" и "an". |
| Вычитание | bn - an | Результатом будет новая последовательность, где каждый элемент получается путем вычитания соответствующих элементов последовательности "an" из элементов последовательности "bn". |
Также можно выполнять умножение и деление бесконечно малой переменной "an" на другую переменную или последовательность.
| Операция | Выражение | Результат |
|---|---|---|
| Умножение | bn * an | Результатом будет новая последовательность, где каждый элемент получается путем умножения соответствующего элемента последовательности "bn" на элемент последовательности "an". |
| Деление | bn / an | Результатом будет новая последовательность, где каждый элемент получается путем деления соответствующего элемента последовательности "bn" на элемент последовательности "an". |
Однако стоит отметить, что не все математические операции возможно выполнять с бесконечно малыми переменными, и не все результаты этих операций могут быть корректно определены.
Примеры использования переменной "an"

Переменная "an" широко применяется в дифференциальном и интегральном исчислении, а также в теории вероятностей и физике, где часто возникают ситуации, требующие рассмотрения бесконечно малых величин.
Примерами использования переменной "an" могут служить следующие задачи и концепции:
- Расчет пределов функций, в которых требуется определить поведение функции при стремлении аргумента к некоторому значению;
- Нахождение производных функций при использовании определения через пределы;
- Описание асимптотических свойств функций и формулирование теорем о предельных значениях;
- Решение дифференциальных и интегральных уравнений, в которых присутствуют бесконечно малые величины;
- Анализ вероятностных распределений и оценка вероятностей событий с использованием асимптотических методов;
- Описание поведения системы при стремлении времени к бесконечности.
В каждом из этих примеров переменная "an" играет роль бесконечно малой величины и позволяет более точно и формально описать и изучить свойства и поведение математических и физических объектов.
Преимущества и недостатки использования переменной "an"

Переменная "an" в математике часто называется бесконечно малой и используется для описания очень малых изменений или приближений величин. Ее использование может иметь как преимущества, так и недостатки.
Преимущества:
| Преимущество | Описание |
|---|---|
| Удобство вычислений | Благодаря использованию бесконечно малых переменных в формулах и уравнениях, вычисления могут быть упрощены и произведены более легко и быстро. |
| Аппроксимация | Переменная "an" позволяет приближать сложные функции более простыми линейными или полиномиальными функциями, что упрощает их анализ. |
| Математические доказательства |
Недостатки:
| Недостаток | Описание |
|---|---|
| Неточность | Использование переменной "an" может привести к неточным результатам, особенно при недостаточной оценке ее малости или при неправильном применении. |
| Затруднения в понимании | Для неподготовленных людей, использование бесконечно малой переменной может быть сложным в понимании, так как она не является обычной числовой переменной. |
| Ошибки вычислений | Некорректное использование переменной "an" может привести к ошибкам вычислений и неверным результатам, особенно при работе с бесконечностями. |
В целом, использование переменной "an" имеет свои преимущества и недостатки, и требует внимательного и правильного применения в математических расчетах и анализе функций.



